Задачи с параметром, решаемые с помощью графического метода
Пример. Найти наименьшее значение функции
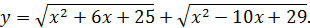
Решение. Выделим полные квадраты в подкоренных выражениях:
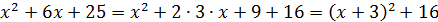 и
и
 .
.
Получим  . Как первое, так и второе слагаемое правой части этого равенства представляет собой расстояние от точки A(x;0) оси абсцисс до некоторой точки с фиксированными координатами, не зависящими от переменной x. Следовательно, решение задачи состоит в нахождении такой точки A оси абсцисс, сумма расстояний от которой до двух данных точек минимальна. Если данные точки B и C находятся по разные стороны от оси абсцисс, то искомая точка есть точка пересечения прямой BC с осью абсцисс, так как для любой другой точки
. Как первое, так и второе слагаемое правой части этого равенства представляет собой расстояние от точки A(x;0) оси абсцисс до некоторой точки с фиксированными координатами, не зависящими от переменной x. Следовательно, решение задачи состоит в нахождении такой точки A оси абсцисс, сумма расстояний от которой до двух данных точек минимальна. Если данные точки B и C находятся по разные стороны от оси абсцисс, то искомая точка есть точка пересечения прямой BC с осью абсцисс, так как для любой другой точки  оси абсцисс сумма расстояний от неё до точек B и C будет больше в силу неравенства треугольника: AB + AC = BC,
оси абсцисс сумма расстояний от неё до точек B и C будет больше в силу неравенства треугольника: AB + AC = BC,  (см. рис.4). Абсциссы точек B и C – это -3 и 5, а квадраты их ординат 16 и 4. Выберем знаки ординат точек B и C так, чтобы эти точки лежали по разные стороны от оси абсцисс: B(-3;-4) и C(5;2). Найдём уравнение прямой BC:
(см. рис.4). Абсциссы точек B и C – это -3 и 5, а квадраты их ординат 16 и 4. Выберем знаки ординат точек B и C так, чтобы эти точки лежали по разные стороны от оси абсцисс: B(-3;-4) и C(5;2). Найдём уравнение прямой BC:




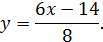
Тогда абсцисса точки A равна



А искомый минимум равен






|
|
| D |

|
| A |
| B |
| C |
Рис.4
Ответ: 10.
Пример. Решить систему уравнений 
Решение. Рассмотрим на координатной плоскости Oxy точки A(0;15), B(8;0), C(0;12), D(16;0). Решить систему – означает найти все точки M(x;y), для каждой из которых MA+MB=17, MC+MD=20. Но AB=  ,CD=
,CD= 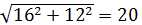 (см. рис.5). Следовательно, MA+MB=AB (т.е. точка M принадлежит отрезку AB),MC+MD=CD(т.е. точка M принадлежит отрезку CD). Поэтому точку M можно найти как точку пересечения отрезков AB и CD, координаты двух точек каждой из которых известны, находятся без труда:
(см. рис.5). Следовательно, MA+MB=AB (т.е. точка M принадлежит отрезку AB),MC+MD=CD(т.е. точка M принадлежит отрезку CD). Поэтому точку M можно найти как точку пересечения отрезков AB и CD, координаты двух точек каждой из которых известны, находятся без труда:
|
|
|
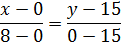
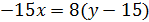
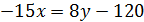

 - уравнение прямой AB;
- уравнение прямой AB;




 - уравнение прямой CD.
- уравнение прямой CD.
Для вычисления абсциссы точки M осталось решить уравнение


 , откуда
, откуда

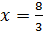 .
.
Ордината точки M находится подстановкой полученной абсциссы в уравнение любой из прямых AB или CD:

| M |
| D |
| C |
| B |
| A |
| 16 |
| 14 |
| 2 |
| 4 |
| 6 |
| 8 |
| 12 |
| 10 |
| 10 |
| 16 |
| 14 |
| 12 |
| 8 |
| 6 |
| 4 |
| 2 |

Рис.5
Ответ:  ).
).
Пример. Найти все значения параметра, при каждом из которых имеет единственное решение система уравнений

Решение. Первое уравнение системы представляет собой уравнение окружности с центром C(0;6) и радиусом 6. Левая часть второго уравнения равна сумме расстояний от точки M(x;y) координатной плоскости Oxy до точек A(0;18) и B(  ;0) этой плоскости. Длина отрезка AB равна
;0) этой плоскости. Длина отрезка AB равна  .
.
|
|
|
MA+MB=AB, следовательно, точка M(x; y) принадлежит отрезку AB. Решение данной задачи заключается в нахождении всех значений параметра  , при каждом из которых существует единственная точка M(x;y) координатной плоскости Oxy, принадлежащая как окружности с центром C(0;6) и радиусом 6, так и отрезку с концами A(0;18) и B(
, при каждом из которых существует единственная точка M(x;y) координатной плоскости Oxy, принадлежащая как окружности с центром C(0;6) и радиусом 6, так и отрезку с концами A(0;18) и B(  ;0). Отсюда следует, что необходимо найти такое положение точки B(
;0). Отсюда следует, что необходимо найти такое положение точки B(  ;0) на оси абсцисс, при котором прямая AB касается окружности в точке M(x;y). Отрезок CM является радиусом, проведённым в точку касания, т.е.
;0) на оси абсцисс, при котором прямая AB касается окружности в точке M(x;y). Отрезок CM является радиусом, проведённым в точку касания, т.е. 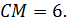 Но
Но  , значит угол
, значит угол  . Поэтому OB=OA
. Поэтому OB=OA  tg
tg  =
=  (где точка O – начало координат). Таким образом,
(где точка O – начало координат). Таким образом,  .
.
| A |
| 18 |
| C |
| 6 |
| B |
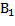
|
| O |
| 0 |

|
| M |
Рис.6
Ответ:  .
.
Пример. Найдите все значения параметра  , при каждом из которых система неравенств
, при каждом из которых система неравенств

имеет хоты бы одно решение на отрезке [3;4].
Решение. Выразим  через
через  :
:
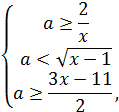
а затем построим графики так, чтобы выполнялось:
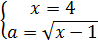 и
и 
| A |

|
|
|
Рис.7
Ответ:  .
.
Пример. Найти все значения параметра  , при каждом из которых следующая система уравнений имеет хотя бы одно решение (x; y; z):
, при каждом из которых следующая система уравнений имеет хотя бы одно решение (x; y; z):

Решение. При любом действительном значении z первое уравнение данной системы является уравнением окружности  плоскости Oxy с радиусом 3 и центром в точке (
плоскости Oxy с радиусом 3 и центром в точке (  ;
;  ), где
), где 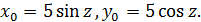 Поскольку
Поскольку  , центр окружности
, центр окружности  лежит на окружности с центром в начале координат и радиусом 5.
лежит на окружности с центром в начале координат и радиусом 5.
Следовательно, множеством всех точек (x; y) плоскости Oxy, координаты которых удовлетворяют первому уравнению данной системы, является кольцо, которое заключено между двумя концентрическими окружностями (включая сами эти окружности) с центром в начале координат и радиусами 2 и 8 (см. рис.8)
| 2 |
| -8 |
| -8 |
| 8 |
| -6 |
| -6 |
| -4 |
| 6 |
| 8 |
| 6 |
| 4 |
| 4 |
| -4 |
| 2 |
| -2 |
| -2 |

Рис.8
Если  , данная система решений не имеет.
, данная система решений не имеет.
Если  , множеством всех точек (x;y) плоскости Oxy, координаты которых удовлетворяют второму уравнению данной системы, является квадрат с диагональю
, множеством всех точек (x;y) плоскости Oxy, координаты которых удовлетворяют второму уравнению данной системы, является квадрат с диагональю  и стороной
и стороной  , который ограничен прямыми:
, который ограничен прямыми:
|
|
|




Данная система имеет хотя бы одно решение только в тех случаях, когда квадрат или вписан в меньшую окружность, которая ограничивает кольцо, тогда  , или описан около большей окружности, которая ограничивает кольцо, тогда
, или описан около большей окружности, которая ограничивает кольцо, тогда  , откуда
, откуда 


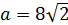 ,
,
либо занимает промежуточное положение между двумя этими положениями, тогда  .
.
Ответ: 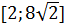 .
.
Пример. Найти все значения параметра  , при каждом из которых хотя бы одно решение неравенства
, при каждом из которых хотя бы одно решение неравенства  принадлежит отрезку [1;2].
принадлежит отрезку [1;2].
Решение. Перепишем неравенство в виде  и раскроем модуль
и раскроем модуль  , как систему
, как систему  .
.
Тогда получаем систему неравенств






Решим уравнение  .
.
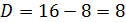
Отсюда получаем, что 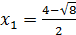 и
и  .
.
Тогда  и
и  . Получаем, что множеством всех точек (x;a) плоскости Oxa, координаты которых удовлетворяют неравенству
. Получаем, что множеством всех точек (x;a) плоскости Oxa, координаты которых удовлетворяют неравенству  является полоса, заключённая между прямыми
является полоса, заключённая между прямыми  и
и  , включая эти прямые.
, включая эти прямые.
Множеством всех точек (x;a) плоскости Oxa, координаты которых удовлетворяют неравенству  , является парабола
, является парабола 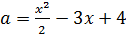 и часть плоскости, которая расположена выше этой параболы (см. рис.9).
и часть плоскости, которая расположена выше этой параболы (см. рис.9).
| 1 |
| -2 |
| -1 |
| 2 |
| 1 |
| 5 |
| 4 |
| 3 |
| 2 |

Рис.9
Система неравенств

имеет хотя бы одно решение на отрезке [1;2] только тогда, когда 
Ответ:  .
.
Пример. Найдите все значения параметра  , при которых неравенство
, при которых неравенство

не имеет решений на отрезке [-3;0].
Решение. Раскроем модуль  по формуле как совокупность
по формуле как совокупность
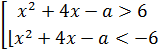
и выразим  через
через  :
:

Построим графики функций  и
и 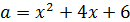 .
.
Для графика  ,
, 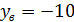 ,
,
для графика  ,
,  .
.
| a |
| A |

Рис.10
Ответ:  .
.
В заключение рассмотрим пример, который решим как аналитическим, так и графическим методом.
Пример. Решить неравенство  .
.
Решение аналитическим методом. Будем решать неравенство  по правилу:
по правилу:

Получаем:

Рассмотрим первую систему: 
1) 

2) 






 и
и 

|
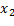
|
Рис.11

3) Найдём при каком 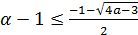



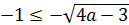




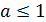 .
.
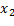
|

|
| -1 |
 , то
, то
Рис.12
решением системы является 
5) Найдём при каком  выполняется система неравенств:
выполняется система неравенств:

6) 
Решением является  .
.
7) 




 .
.
Подведём итог, что:
если  , то
, то  ;
;
если  , то
, то  .
.
Рассмотрим вторую систему: 
1) 

2) 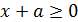

Поведём итог, что:
если  , т.е.
, т.е. 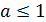 , то система не имеет решений;
, то система не имеет решений;
если  , т.е.
, т.е.  , то
, то  .
.
Заметим, что  равен
равен  .
.
Ответ: если  , то
, то  ; если
; если  , то
, то 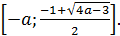
Решение графическим методом. Построим прямую  ,и рассмотрим три случая расположения графика
,и рассмотрим три случая расположения графика  относительно этой прямой.
относительно этой прямой.
1) Если график  расположен ниже
расположен ниже  , то решений нет. (см. рис.13 положение 1)
, то решений нет. (см. рис.13 положение 1)
2) Составим систему

которая должна иметь одно решение, что равносильно для уравнения
 иметь один корень.
иметь один корень.


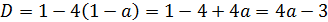
 , тогда
, тогда
 и
и  , а также
, а также


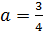 .
.
Отсюда получаем, что при  решений нет. (см. рис.13 положение 2)
решений нет. (см. рис.13 положение 2)
3)  и
и  имеют две общие точки.
имеют две общие точки.
Такое положение достигается при 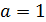 . (см. рис. 13 положение 3)
. (см. рис. 13 положение 3)
Теперь мы можем сделать вывод, что:
если  , то
, то  – решение, где
– решение, где  и
и  - абсциссы точек пересечения графиков;
- абсциссы точек пересечения графиков;
если  ,то
,то  – решение, где
– решение, где  - больший из корней
- больший из корней  и
и  . (см. рис. 13 положение 4)
. (см. рис. 13 положение 4)
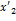
|
- 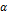
|

|

|
| -1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 1 |

Рис.13
Ответ: если  , то
, то  ; если
; если  , то
, то 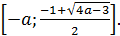
Заключение
Цель данной работы состояла в изучении задач с параметрами в материалах государственной итоговой аттестации и методов их решения.
Изучив и проанализировав задачи с параметрами в материалах ЕГЭ по математике за последние пять лет, было выявлено, что в большинстве случаев встречаются задачи первого типа рассмотренной нами классификации. Для решения этих задач в основном используются аналитический и графический методы.
Данные методы были рассмотрены на разных типах задач. Аналитический метод – это решение задачи, позволяющее с помощью математических преобразований упростить выражение и найти ответ. Графический метод – нахождение решения и ответа задачи с параметром с помощью координатной плоскости.
Необходимо уметь решать данные задачи различными методами, чтобы выбрать наиболее эффективный для решения конкретной задачи.
Для закрепления навыков решения задач с параметром была подобрана серия задач с параметром, среди которой преобладают задачи первого типа, и решение которых выполняется аналитическим и графическим методами.
Список литературы
1. Беляева Э. С. Математика. Уравнения и неравенства с параметром. В 2 ч. Ч.1: учебное пособие/ Э.С. Беляева, А.С. Потапов, С.А. Титаренко. ̶ М.: Дрофа, 2009. ̶ 480 с.
2. Высоцкий В. С. Задачи с параметрами при подготовке к ЕГЭ. – М.: Научный мир, 2011. – 316с.: 262 ил.
3. Голубев В. И. Решение сложных и нестандартных задач по математике. – М.: ИЛЕКСА, 2007. – 252 с.
4. Горнштейн П. И. Задачи с параметрами / П. И. Горнштейн, В. Б. Полонский, М. С. Якир. ̶ 3-е изд., доп. и перераб. ̶ М.: Илекса, Харьков: Гимназия, 2005. ̶ 328 с.
5. Здоровенко М. Ю., Зеленина Н. А., Крутихина М. В. Использование различных методов решения задач с параметром на Едином государственном экзамене по математике // Научно-методический электронный журнал «Концепт»: - 2016. - №8 (август). – 0,4 п.л. – URL: https://e-koncept.ru/2016/16176.htm
6. Крамор В. С. Задачи с параметром и методы их решения / В. С. Крамор. – М.: ООО Из-во Оникс: ООО Из-во Мир и Образование, 2007. – 416с.: ил.
7. Локоть В. В. Задачи с параметрами. Линейные и квадратные уравнения, неравенства, системы: Учебное пособие. – 2-е изд., испр. и доп. – М.: АРКТИ, 2005. – 96 с.
8. Корянов А. Г., Прокофьев А. А. Математика ЕГЭ 2011. Типовые задания С5. Уравнения и неравенства с параметрами: количество решений [Электронный ресурс]. ̶ Режим доступа: http://alexlarin.net/ege/2011/c52011.pdf
9. Мантуров О. В., Солнцев Ю. К. , Соркин Ю. И., Федин Н. Г. Толковый словарь математических терминов. Пособие для учителя. – М.: Из-во Просвещение, 1965. – 542 с.
10. Мирошин В. В. Решение задач с параметрами. Теория и практика / В.В. Мирошин. ̶ М.: Издательство «Экзамен», 2009. ̶ 286 с.
11. Прокофьев А. А. Задачи с параметрами. ̶ М.: МИЭТ, 2004. ̶ 258 с.
12. Фалилеева М. В. Первые шаги в решении уравнений и неравенств с параметром: Учебное пособие / М.В. Фалилеева. – Казань: Казан. ун-т, 2014. – 111 с.
13. Шестаков С. А. ЕГЭ 2016. Математика. Задачи с параметром. Задача 18 (профильный уровень) / Под ред. И.В. Ященко. – М.: МЦНМО, 2016. – 240 с.
14. Ястребинецкий Г. А. Задачи с параметрами. ̶ М.: Просвещение, 1986. ̶ 127 с.
15. http://alexlarin.net/
16. http://www.fipi.ru/
Дата добавления: 2018-06-27; просмотров: 619; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
