Сравнительный анализ задач с параметром демоверсий ЕГЭ по математике ФИПИ с вариантами досрочного и основного этапа ЕГЭ
Задача с параметром в демоверсии Федерального института педагогических измерений 2017 года выглядит следующим образом:
Найдите все положительные значения  , при каждом из которых система
, при каждом из которых система

имеет единственное решение. [16]
Такая же задача представлена в демоверсиях ФИПИ 2016 и 2015 годов.
В демоверсии ФИПИ как 2014 года, так и 2013 года задача с параметром представлена так:
Найдите все значения  , при каждом из которых наименьшее значение функции f (x) = 2ax +
, при каждом из которых наименьшее значение функции f (x) = 2ax +  больше 1. [16]
больше 1. [16]
В вариантах досрочного периода ЕГЭ по математике встречались следующие задачи с параметром:
В 2017 году –
Найдите все значения параметра  , при каждом из которых система неравенств
, при каждом из которых система неравенств 
имеет хотя бы одно решение на отрезке  [15]
[15]
В 2016 году –
Найдите все значения параметра  , при каждом из которых система уравнений
, при каждом из которых система уравнений 
имеет ровно два различных решения. [15]
В 2015 году –
Найдите все значения параметра  , при каждом из которых система уравнений
, при каждом из которых система уравнений 
имеет единственное решение. [15]
В 2014 году –
Найдите все значения  , при которых уравнение
, при которых уравнение
2  =
=  имеет единственное решение. [15]
имеет единственное решение. [15]
В 2013 году –
Найдите все значения  , для каждого из которых уравнение
, для каждого из которых уравнение

имеет хотя бы один корень, принадлежащий промежутку [-1;1). [15]
Варианты основного этапа ЕГЭ по математике содержали следующие задачи с параметром:
В 2017 году –
Найдите все значения  , при каждом из которых уравнение
, при каждом из которых уравнение
|
|
|



 имеет ровно один корень на отрезке
имеет ровно один корень на отрезке  . [15]
. [15]
В 2016 году –
Найдите все значения  , при каждом из которых уравнение
, при каждом из которых уравнение
 =
=  имеет ровно три различных значения. [15]
имеет ровно три различных значения. [15]
В 2015 году –
Найдите все значения параметра  , при каждом из которых система уравнений
, при каждом из которых система уравнений

имеет более двух решений. [15]
В 2014 году –
Найдите все значения параметра  , при каждом из которых уравнение
, при каждом из которых уравнение
 имеет ровно два решения. [15]
имеет ровно два решения. [15]
В 2013 году –
Найдите все значения  , при каждом из которых уравнение
, при каждом из которых уравнение
 =
=  имеет единственный корень. [15]
имеет единственный корень. [15]
Рассмотрев и сравнив вышеизложенные задачи с параметром из вариантов демоверсий ФИПИ, досрочного и основного этапа ЕГЭ за последние пять лет можно сделать выводы о том, что задачи с параметром демоверсий ФИПИ во всех случаях совпадают с задачами досрочного и основного этапа ЕГЭ и относятся к первому типу, описанному нами выше.
Поскольку были рассмотрены единичные варианты основного этапа ЕГЭ, не исключено, что в них встречались также и задачи с параметром второго типа.
Это позволяет сделать вывод о том, что для успешного выполнения задач с параметром на ЕГЭ, учащиеся должны уметь решать данные задачи различных типов и видов, а не бездумно запоминать типовые.
|
|
|
Основные методы решения задач с параметром
Традиционно для решения задач с параметрами используются аналитический и графический методы. [5]
Аналитический метод
Аналитический метод является не только самостоятельным методом решения задач, но и обязательной составной частью всех остальных методов. Основной частью аналитического метода решения задач является метод эквивалентных или равносильных преобразований. Предлагаемый подход к решению уравнений и неравенств с параметрами, их систем или совокупностей основан на замене одного математического высказывания другим равносильным математическим высказыванием. Задача рассматривается как некоторое логическое высказывание, область истинности которого предстоит установить в результате его рассмотрения. При этом исходное условие рядом равносильных преобразований или преобразований следствий приводится к совокупности простейших логических утверждений, истинность или ложность которых считается установленной.
В аналитическом методе решения задач чаще всего используется приём дробления – разделение условия задачи на совокупность более простых условий. Так, условие задачи, содержащие выражения, стоящие под знаками модуля, обычно разделяют на совокупность более простых условий, не содержащих модуль. [10, стр.61]
|
|
|
Рассмотрим решение задачи с параметром из типовых экзаменационных вариантов по математике аналитическим способом:
Пример. При каждом значении параметра  решить неравенство
решить неравенство
 .
.
Решение. Данное неравенство является линейным относительно переменной x.
Раскроем скобки 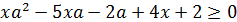 , перегруппируем слагаемые и приведём его к стандартному виду: (
, перегруппируем слагаемые и приведём его к стандартному виду: ( 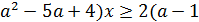 ). Корнями квадратного трёхчлена в левой части полученного неравенства являются числа
). Корнями квадратного трёхчлена в левой части полученного неравенства являются числа
 и
и  , поэтому, разложив этот трёхчлен на линейные множители, придём к неравенству (
, поэтому, разложив этот трёхчлен на линейные множители, придём к неравенству ( 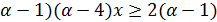 .
.
Коэффициент при переменной в левой части неравенства в зависимости от значений параметра может быть равен нулю, положителен или отрицателен.
Рассмотрим все возможные случаи.
Если  , неравенство принимает вид 0
, неравенство принимает вид 0  и выполняется при любом значении переменной x.
и выполняется при любом значении переменной x.
Если  , неравенство принимает вид 0
, неравенство принимает вид 0  и не выполняется ни при каких значениях x.
и не выполняется ни при каких значениях x.
Если (  )(
)(  )
)  , т.е.
, т.е.  , то, разделив обе части неравенства на положительное число (
, то, разделив обе части неравенства на положительное число (  и сократив дробь в правой части, получим
и сократив дробь в правой части, получим  , т.е.
, т.е.  .
.
Если (  , т.е.
, т.е. 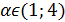 , то, разделив обе части неравенства на отрицательное число (
, то, разделив обе части неравенства на отрицательное число (  и сократив дробь в правой части, получим
и сократив дробь в правой части, получим  , т.е.
, т.е.  .
.
|
|
|
Ответ:  при
при  ; (
; (  ) при
) при  ; (
; (  при
при  ; нет решений при
; нет решений при  .
.
Графический метод
Любая задача с параметрами есть задача как минимум с двумя переменными – аргументом и параметром. Следовательно, решение задачи - упорядоченный набор их значений, может рассматриваться как координаты точки некоторого евклидова пространства.[10, стр.62]
Учитывая роль параметра в задаче, выделяют два основных графических приема: первый – построение графического образа на координатной плоскости Oxy, второй – на координатной плоскости Oxa.
Первый прием заключается в том, что исходное уравнение (или неравенство) преобразуют к виду  На плоскости Oxy строится график функции
На плоскости Oxy строится график функции  . Функция
. Функция  задает определенное семейство кривых, зависящих от параметра
задает определенное семейство кривых, зависящих от параметра  . Кривые этого семейства получаются из кривой
. Кривые этого семейства получаются из кривой 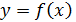 с помощью некоторого элементарного преобразования (параллельного переноса вдоль осей, растяжения, наложения модуля или в случае линейной зависимости между x и
с помощью некоторого элементарного преобразования (параллельного переноса вдоль осей, растяжения, наложения модуля или в случае линейной зависимости между x и  - поворота относительно некоторой точки). Построив графический образ уравнения
- поворота относительно некоторой точки). Построив графический образ уравнения  можно установить, сколько точек пересечения имеют графики функций
можно установить, сколько точек пересечения имеют графики функций  и
и  , - это определяет количество корней уравнения
, - это определяет количество корней уравнения  , а, следовательно, и исходного уравнения в зависимости от значения параметра. Так же для неравенства
, а, следовательно, и исходного уравнения в зависимости от значения параметра. Так же для неравенства  можно выяснить, что представляет собой множество его решений.[11, стр.55]
можно выяснить, что представляет собой множество его решений.[11, стр.55]
Используя второй прием, исходное уравнение (или неравенство) преобразуют к виду  (или
(или  ). На плоскости Oxa строят график функции
). На плоскости Oxa строят график функции 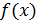 , а далее, пересекая полученный график прямыми, параллельными оси
, а далее, пересекая полученный график прямыми, параллельными оси  , получают необходимую информацию.
, получают необходимую информацию.
Подобные приемы используют и в случае систем:
уравнений 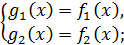
неравенств 
уравнения и неравенства 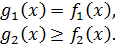
Для этого строят графический образ системы и интерпретируют его в зависимости от значения параметра и условий задачи. [11, стр.56]
Рассмотренный метод лучше всего работает, если условие задачи содержит вопрос о количестве корней в зависимости от значений параметра или определения значений параметра, при которых решение отсутствует или единственно.
Пример. Найти все значения параметра  , при каждом из которых система неравенств
, при каждом из которых система неравенств  имеет хотя бы одно решение, и укажите решения системы для каждого значения
имеет хотя бы одно решение, и укажите решения системы для каждого значения  .
.
Решение. Приведём данную систему к виду

и построим в системе координат Oxa графики функций  (прямая, проходящая через точки (4;0) и (3;12)),
(прямая, проходящая через точки (4;0) и (3;12)), 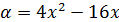 (парабола, ветви которой направлены вверх, с вершиной в точке (2; -16), пересекающая ось абсцисс в точках (0;0) и (4;0)),
(парабола, ветви которой направлены вверх, с вершиной в точке (2; -16), пересекающая ось абсцисс в точках (0;0) и (4;0)),  (прямая, проходящая через точки (0;0) и (3;12)). Множество всех точек (x;a) плоскости Oxa, удовлетворяющих данной системе, покажем штриховкой. Для записи ответа будем рассматривать различные положения считывающей прямой.
(прямая, проходящая через точки (0;0) и (3;12)). Множество всех точек (x;a) плоскости Oxa, удовлетворяющих данной системе, покажем штриховкой. Для записи ответа будем рассматривать различные положения считывающей прямой.
При  или
или  считывающая прямая не имеет с заштрихованной областью ни одной общей точки.
считывающая прямая не имеет с заштрихованной областью ни одной общей точки.
При  считывающая прямая имеет с заштрихованной областью единственную общую точку – вершину параболы (т.е. решением данной системы является
считывающая прямая имеет с заштрихованной областью единственную общую точку – вершину параболы (т.е. решением данной системы является  , при
, при  эта прямая имеет с заштрихованной областью также единственную общую точку – точку пересечения прямых
эта прямая имеет с заштрихованной областью также единственную общую точку – точку пересечения прямых  и
и  (т.е. решением данной системы является
(т.е. решением данной системы является  ).
).
При 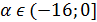 считывающая прямая пересекает заштрихованную область по отрезку, концы которого лежат на параболе
считывающая прямая пересекает заштрихованную область по отрезку, концы которого лежат на параболе  В этом случае левый конец отрезка является меньшим корнем уравнения
В этом случае левый конец отрезка является меньшим корнем уравнения  (этот корень равен
(этот корень равен  ), а правый – большим корнем этого уравнения (он равен
), а правый – большим корнем этого уравнения (он равен  ).
).
При  считывающая прямая пересекает заштрихованную область по отрезку, левый конец которого лежит на прямой
считывающая прямая пересекает заштрихованную область по отрезку, левый конец которого лежит на прямой  (и, значит,
(и, значит,  ), а правый – на прямой
), а правый – на прямой  (и, значит,
(и, значит,  ).
).
| x |
| y |
| -14 |
| -16 |
| -12 |
| -10 |
| -8 |
| -6 |
| -4 |
| -2 |
| 0 |
| 14 |
| 12 |
| 10 |
| 8 |
| 6 |
| 4 |
| 2 |
| 4 |
| 3 |
| 2 |
| 1 |

Рис.1
Ответ: решений нет при  ;
;  при
при  ;
;  при
при  ;
;  при
при  ;
;  при
при  .
.
Подбор задач с параметром
Дата добавления: 2018-06-27; просмотров: 389; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
