Тема 5 «Средние величины и показатели вариации»

Цель - приобретение навыков расчета средних величин и показателей вариации с использованием экономически обоснованных формул.

Содержание темы:

Вычисление средних величин как важный прием статистического исследования. Сущность средних величин. Виды средних величин и их формы. Простые и взвешенные средние. Выбор вида и формы средней.

 Свойства средней арифметической и их использование при расчете средней.

Структурные средние величины: мода, медиана, их смысл и методика расчета в дискретных и интервальных рядах. Понятие ассиметрии, виды и методы определения (графический и математический).

Понятие о вариации. Анализ причин, порождающих вариацию признака. Показатели вариации абсолютные, относительные и средние. Дисперсия признака. Коэффициент вариации как мера типичности средней.

Методические указания:

Студентам следует уяснить, что средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности. Средние величины используются на этапе обработки и обобщения полученных первичных статистических данных.

Необходимо обратить внимание, что существует 2 класса средних величин: степенные и структурные.

Наиболее часто в статистическом анализе применяются степенныесредниевеличины различных видов.

Степенные средние величинымогут быть простыми и взвешенными.

Простая средняя величина рассчитывается по несгруппированным статистическим данным.Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам.

Конкретные формулы для расчета каждого вида степенных средних величин и методика их выбора рассматриваются ниже.

 

Таблица 1 - Виды и формы средних величин

Виды средних величин	Простая	Номер формулы	Взвешенная	Номер формулы
1	2	3	4	5
1. Арифметическая		(5.1)		(5.2)
2. Гармони­ческая		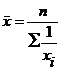(5.3)		(5.4)
3. Квадра­тическая		(5.5)		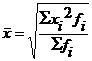(5.6)
4. Геомет­рическая		(5.7)		(5.8)
1. Хроноло-гическая		(5.9)	…

Основные обозначения:

 - среднее значение признака;

х_i - индивидуальные значения осредняемого признака;

n - количество единиц совокупности;

f_i - частота (вес) индивидуальных значений осредняемого признака;

w_i = x_if_i - произведение индивидуального значения признака и его частоты.

Для осреднения различных признаков используются разные виды средних величин. Выбор вида средней осуществляется индивидуально в каждом случае и зависит от наличия исходных данных и вида признака.

Чаще всего используются простая и взвешенная арифметическая средняя.

В том случае, когда нет данных о частотах отдельных признаков, но имеются сведения о произведении индивидуального значения признака на его частоту, среднюю арифметическую можно заменить средней гармонической. При этом гармоническая простая используется только тогда, когда равны объемы совокупностей.

Средняя квадратическая, простая и взвешенная, используется, как правило, для расчета средних отклонений.

Геометрическая средняя используется для осреднения таких признаков, для которых характерна мультипликативная зависимость. Чаще всего гармоническая средняя используется для расчета средних темпов роста и средних индексов.

Хронологическая средняя применяется для расчетов средних уровней в моментных рядах динамики.

 

К структурным средним относятся мода и медиана.

Мода(Мо) - это наиболее часто встречающееся значение призна­ка, или, говоря иначе, значение варианты с наибольшей частотой.

В дискретных рядах модой является значение признака в той группе, у которой наблюдается наибольшая частота. Определить моду в этом случае можно визуально.

В интервальных рядах распределения мода также находится в той группе, которая имеет наибольшую частоту. Но так как в интервальных рядах признак может принимать любое значение в заданном интервале, точное дискретное значение моды  следует определять по специальной формуле:

 

 

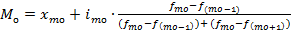 (5.10)

 

где х_мо - нижняя граница модального интервала;

i_мо - величина модального интервала;

f_мо- частота модального интервала;

f_(мо-1)- частота интервала, предшествующего модальному;

f_(мо+1) - частота интервала, следующего за модальным.

 

Модальным является интервал, имеющий максимальную частоту.

Значение моды, рассчитанное по формуле (5.10), не может быть меньшим, чем нижняя граница модального интервала, и не будет превышать верхнюю границу модального интервала.

 

Медианой(Ме) называется значение варианты, находящейся в центре ранжированного вариационного ряда. Медиана делит вариационный ряд на две равные час­ти. При этом 50% единиц совокупности имеют значение меньше медианного, а 50% — больше медианного.

В дискретном ряду распределения медиана равна значению признака в той группе, у которой сумма накопленных частот равна или превышает половину суммы всех частот ряда распределения.

Сумма накопленных частот находится последовательным сложением частот каждой группы. Так, для первой группы сумма накопленных частот будет равна частоте этой группы, для второй группы - сумме частот первой и второй группы, для третьей группы - сумме частот первой, второй и третьей группы и т.д. накопленная частота последней группы будет равна общей сумме частот ряда распределения.

В интервальном ряду распределения медиана  находится по специальной формуле:

(5.11)

 

где х_ме - нижняя граница медианного интервала;

i_ме- величина медианного интервала;

f_ме - частота медианного интервала;

Σf - сумма всех частот ряда распределения;

S_ме-1- сумма частот, накопленных до медианного интервала.

 

Медианным считается интервал, сумма накопленных частот которого равна или превышает половину всех частот ряда распределения.

Значение медианы будет не меньше, чем значение нижней границы медианного интервала, и не превысит значения верхней границы медианного интервала.

 

Показатели вариации неразрывно связаны со средними величинами и дополняют обычно расчет средних величин в социально-экономическом и финансовом анализе.

 Вариация - это различие значений величин признака (X) у отдельных единиц статистической совокупности. Для изучения силы вариации рассчитывают систему обобщающих показателей вариации.

Для характеристики размера вариации признака используются абсолютные и относительные показатели. К абсолютным показателям относятся:

1. Размах вариации ( 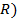. Определяется по формуле:

 

(5.12)

где x_max, x_min - максимальное и минимальное значение признака в изучаемой совокупности.

 

2. Среднее линейное отклонение ( 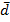). Показывает, на сколько единиц в среднем индивидуальные значения признака отклоняются от его среднего значения.

Имеет простую и взвешенную форму. Простая форма применяется для несгруппированных данных, взвешенная - если данные сгруппированы. Форма расчета совпадает с формой расчета средней величины.

В простой форме среднее линейное отклонение 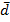 рассчитывается по формуле:

 

(5.13)

 

Взвешенная форма имеет вид:      

 

(5.14)

 

Следует иметь виду, что отклонение реальных значений от средней берется по модулю. В противном случае сумма отклонений будет равна 0.    

 

3. Среднее квадратическое отклонение . Показывает, на сколько единиц в среднем индивидуальные значения признака отклоняются от средней, но сумма отклонений возводится в квадрат. Рассчитывается также в простой (5.15) и взвешенной форме (5.16).

 

(5.15)

 

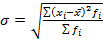 (5.16)

 

4. Дисперсия ( . Представляет собой сумму квадратов отклонений индивидуальных значений признака от средней. Данный показатель не имеет единиц измерения. В простой форме дисперсия имеет вид:

 

(5.17)

 

Во взвешенной форме:

 

(5.18)

 

Можно рассчитать дисперсию по методу моментов. В этом случае расчет производится по формуле:

 

(5.19)

 

При сравнении колеблемости различных признаков в одной и той же совокупности, или же при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической, используются относительные показатели вариации. Они вычисляются как отношение абсолютных показателей вариации к средней арифметической (или медиане) и чаще всего выражаются в процентах. К ним относят:

· коэффициент осцилляции;   

· относительное линейное отклонение; 

· коэффициент вариации.

Коэффициент осцилляции 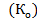 рассчитывается как отношение размаха вариации к среднему значению признака (в процентах):

 

                                       (5.20)

 

Относительное линейное отклонение( ) находится как частное от деления среднего линейного отклонения на среднее значение признака ( в процентах):

 

(5.21)       

 

Коэффициент вариации ( )является мерой типичности средней и показывает, на сколько процентов в среднем индивидуальные значения признака отклоняются от средней. Он находится по формуле:

 

(5.22)          

 

Наиболее популярным из этой группы показателей являетсякоэффициент вариации.Его при­меняют не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность счи­тается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).

Вопросы для самоконтроля:

1. Сформулируйте, в чем заключается сущность средних величин. Каковы основные виды и формы средних величин?

2. Какие основные правила расчета средней величины необходимо выполнить, чтобы полученная средняя была реальной, а не формальной?

3. Перечислите основные свойства средней арифметической.

4. Как в статистике трактуют понятия «мода» и «медиана». К какому виду средних они относятся?

5. Каковы особенности определения моды и медианы в дискретном ряду распределения?

6. Каковы особенности определения моды и медианы в интервальном ряду распределения?

7. Что представляет собой вариация признака и в чем состоит значение ее применения?

8. Какие обобщающие показатели вариации характеризуют абсолютный размер колеблемости признака около средней величины?

9. Что такое дисперсия? Каковы виды дисперсий? В чем сущность правила сложения дисперсий?

Литература:[2], [4], [5], [8], [10], [11], [12], [13], [14].

Интернет – ресурсы: [1], [6].

 

 

---

Дата добавления: 2018-06-01; просмотров: 521; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!