Тема 8 «Индексный анализи его использование при анализе цен и инфляции»

Цель - освоение методик факторного и динамического анализа с применением статистических индексов, изучение приемов анализа уровня инфляции.

Содержание темы:

Роль индексов в экономическом анализе. Классификация индексов.

Способы построения общих индексов. Агрегатная форма индексов. Определение абсолютного изменения показателей на основе агрегатных индексов.

 Средние арифметические и средние гармонические индексы.

Индексный анализ динамики средних показателей. Индексы переменного и фиксированного состава, индексы структурных сдвигов.

Индексный метод определения влияния факторов на результативный признак. Построение системы взаимосвязанных индексов.

Организация наблюдения за ценами и тарифами в РФ. Направления наблюдения за ценами. Методы расчета индексов цен.

Методические указания:

Статистический индекс – это относительный показатель, который характеризует изменение уровня какого-либо явления во времени или его соотношение в пространстве.

Для определения индекса следует произвести сопоставление не менее двух величин. При этом в числителе располагают сравниваемую величину, а в знаменателе – базу сравнения.

Студентам следует уяснить, что основным элементом индексного отношения является индексируемая величина, под которой понимается значение признака, изменение которого является объектом статистического изучения.

Измеряются индексы в коэффициентах (долях единицы) или в процентах.

По степени охвата элементов совокупности индексы делятся на:

· индивидуальные индексы

· общие (сводные) индексы

Индивидуальные индексы позволяют определить изменение простого явления во времени. Они равны соотношению уровня явления у отдельной единицы совокупности в отчетном и базисном периодах:

 

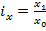(8.1)

 

где х₁, х₀ – значение признака у отдельной единицы совокупности в отчетном и базисном периодах.

Индивидуальные индексы бывают цепными и базисными, в зависимости от того, уровень какого периода принимается за базисный.

Общие (сводные) индексы позволяют определить изменение сложного явления во времени, а также выявить влияние факторов на изменение данного сложного явления. Сложным считается явление, отдельные элементы которых не подлежат непосредственному суммированию. Для достижения сопоставимости сложных явлений при их индексации используется дополнительная величина – соизмеритель, который подбирается индивидуально к каждой индексируемой величине. Следует обратить особое внимание на то, что при перемножении индексируемой величины и соизмерителя получался новый экономический показатель. Соизмеритель в общем индексе не изменяется, он всегда зафиксирован на определенном уровне.

Общие индексы ( )имеют вид:

 

где х₁, х₀ – значение индексируемой величины у отдельных единиц совокупности в отчетном и базисном периодах;

f– фиксированное значение соизмерителя.

Общие (сводные) индексы по форме расчета делятся на агрегатные и средние.

Агрегатная форма – основная форма существования общих индексов. Как и все общие индексы, агрегатные индексы состоят из двух элементов – индексируемой величины и соизмерителя, при этом соизмеритель фиксируется на определенном уровне. В зависимости от того, на каком уровне фиксируется соизмеритель, различают следующие виды агрегатных индексов:

· индекс Ласпейреса, в котором соизмеритель зафиксирован на базисном уровне;

· индекс Пааше, в котором соизмеритель зафиксирован на отчетном уровне;

·  «идеальный» индекс Фишера. Он является средней геометрической из произведения индексов Пааше и Ласпейреса.

Следует иметь ввиду, что в экономическом анализе чаще всего используют только первые два индекса.

Индекс Ласпейреса( ). Соизмеритель фиксируется на базисном уровне и индекс имеет вид:

 

 (8.3)

Индекс Пааше . Соизмеритель фиксируется на отчетном уровне и индекс имеет вид:

(8.4)

Формулы для расчетов основных индивидуальных и агрегатных индексов приведены в таблице2.

Следует иметь в виду, что индексируемая величина и соизмеритель могут меняться ролями: индексируемая величина становится соизмерителем и фиксируется на определенном уровне, а соизмеритель может выступать индексируемой величиной. Например, можно индекс цен Ласпейреса, который показывает среднее изменение цен, преобразовать в индекс физического объема продукции , который показывает среднее изменение физического объема произведённой продукции:

 

(8.5)

Еще одно назначение агрегатных индексов – определение абсолютного отклонения показателей. Для этого из числителя соответствующего агрегатного индекса следует отнять его знаменатель.

Например, если требуется определить абсолютное изменение товарооборота, из числителя агрегатного индекса товарооборота отнимают его знаменатель:

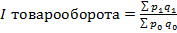(8.6)

 

тогда абсолютное изменение товарооборота ( ) определяется по формуле:

 (8.7)

 

Таблица 2 - Основные виды индексов

Наименование индекса	Индексируемая величина	Индивидуальный индекс	Соизмеритель	Агрегатный индекс
1	2	3	4	5
1. Индекс цен	р - цена единицы продукции		q – количество проданной продукции
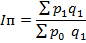
2. Индекс производительности труда	w-выработка одного работника		Ч – численность работников
3. Индекс затрат труда на производство	t-затраты времени на производство единицы продукции		q – количество произведенной продукции
4. Индекс себестоимости продукции	z-себестоимость единицы продукции		q – количество произведенной продукции

 

Помимо агрегатных индексов, в статистике используется средняя форма индекса. Для определения среднего индекса используют формулы средней арифметической взвешенной и средней гармонической взвешенной.

Средние индексы получают путем преобразования агрегатного индекса Пааше или Ласпейреса.

Средний арифметический       индекс получается в том случае, когда производят преобразования индекса Ласпейреса. К данной форме индекса следует прибегать в тех случаях, когда есть данные об индивидуальных индексах индексируемой величины. В этом случае производится преобразование числителя агрегатного индекса по следующей схеме:

 

(8.8)

 

так как из формулы индивидуального индекса (8.1) следует, что   

 

(8.9)

 

Как видно из формулы (8.8), весами среднего арифметического индекса выступает обобщающий показатель, зафиксированный на уровне базисного периода .

Средний гармонический индекс получается путем преобразования в средний агрегатного индекса Пааше, исходя из того, что

 

(8.10)

 

Тогда, формула (8.4) преобразуется следующим образом:

 

(8.11)

 

Средний гармонический индекс используется тогда, когда известен уровень обобщающего явления в отчетном периоде .

Одно из назначений индексного анализа – выявление роли факторов на изменение обобщающего показателя. Для этого строится система взаимосвязанных индексов. Взаимосвязь индексов определяется следующим правилом - индексы связаны между собой так же, как связаны между собой индексируемые величины.

       Так, если обобщающий показатель равен произведению двух факторных признаков, то и индекс обобщающего показателя будет равен произведению индексов факторных признаков.

Если    (8.12),

то        (8.13)

Использование данного правила позволяет определить влияние факторов на динамику обобщающего показателя. Для определения совместного влияния факторов используется следующий индекс обобщающего показателя, называемый индексом переменного состава ( :

(8.14)

где х – качественный признак;

f – количественный признак.

Определить влияние каждого из факторов на динамику обобщающего показателя можно, если индексы факторных признаков увязать в систему. Система будет построена правильно только в том случае, если один из факторных индексов примет вид агрегатного индекса Ласпейреса, а второй – агрегатного индекса Пааше.

Чтобы определить, как правильно построить систему, пользуются следующей схемой:                         

 1.   Все показатели делятся на количественные (структурные) и качественные.

2.    В первую очередь изменяются количественные показатели. Качественные показатели служат соизмерителями и фиксируются на базисном уровне.

3.    Во вторую очередьизменяются качественные показатели. Количественные (или структурные) показатели выступают соизмерителями и фиксируются на отчетном уровне.

4.    Качественными считаются показатели, отражающие размер явления у одной единицы совокупности, например, выработка 1 работника, затраты на единицу изделия, стоимость единицы товара и т.д.

 

Применение данных правил позволяет построить следующие агрегатные индексы факторных признаков:

1. Индекс количественного признака (I_f):

 

 (8.15)

 

Данный индекс имеет двойственное назначение. Во-первых, он показывает, во сколько раз в среднем изменился количественный признак в совокупности. Во-вторых, он показывает, во сколько раз в среднем изменился обобщающий показатель за счет изменения количественного признака.

2. Индекс качественного признака (I_х):

 

(8.16)

 

Данный индекс также имеет двойственное назначение. Во-первых, он показывает, во сколько раз в среднем изменился качественный признак в совокупности. Во-вторых, он показывает, во сколько раз в среднем изменился обобщающий показатель за счет изменения качественного признака.

Общее изменение обобщающего показателя можно найти из следующего равенства:

(8.17)

 

Базируясь на данной системе взаимосвязанных индексов, можно определить абсолютное изменение обобщающего показателя и выявить влияние факторов на его изменение в абсолютном выражении. Для этого из числителя соответствующего индекса отнимают его знаменатель. Абсолютное изменение обобщающего показателя покажет формула (8.18):

 

 (8.18)

 

Формула (8.19) покажет абсолютное изменение обобщающего показателя за счет изменения количественного признака( .

 

 (8.19)

 

Формула (8.20) покажет абсолютное изменение обобщающего показателя за счет изменения качественного признака .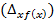

 

(8.20)

 

Общее изменение обобщающего показателя можно найти из следующего равенства:

 

(8.21)

 

Система взаимосвязанных индексов может применяться и для анализа причин изменения среднего значения признака. С этой целью строится система из трех взаимосвязанных индексов:

· переменного состава, показывающего изменение среднего значения признака;

· постоянного состава, характеризующего изменение среднего значения признака за счет изменения индивидуальных значений признаков у всех единиц совокупности;

· структурных сдвигов, характеризующий изменение средней за счет изменения долей отдельных единиц в общем объеме совокупности. 

Индексный анализ широко применяется на практике для изучения динамики цен на различные группы товаров и услуг. Основным индикатором изменения цен в любой стране является индекс потребительских цен (ИПЦ).

Индекс потребительских цен характеризует изменение во времени общего уровня цен на товары и услуги, приобретаемые населением для непроизводственного потребления. Он исчисляется как отношение стоимости фактического фиксированного набора товаров и услуг в текущем периоде к его стоимости в базисном периоде. В настоящее время ИПЦ является индикатором уровня инфляции.

Фиксированный набор товаров и услуг – это репрезентативная выборка групп товаров и услуг, наиболее часто потребляемых населением. Такой набор одинаков для всех регионов России. В него включаются три группы: продовольственные товары, непродовольственные товары и платные услуги населению.

Расчет ИПЦ производится ежемесячно и ежеквартально на базе статистических данных, полученных в ходе наблюдения за ценами. Кроме того, для расчета ИПЦ используют данные о структуре фактических потребительских расходов населения за предыдущий период.

Расчет сводного ИПЦ на федеральном и региональных уровнях производится еженедельно. Для определения индекса за более продолжительный период (месяц, квартал и т.д.) используется цепной метод, т.е. перемножаются ИПЦ недельные (месячные и т.д.). Более детально методика расчета ИПЦ приводится в пособии [5] на стр. 90-95.

 

Вопросы для самоконтроля:

1. Для решении каких задач статистика использует индексный метод анализа?

2. Дайте понятие индекса. Каковы основные принципы построения статистических индексов?

3. Каковы основные принципы расчета сводных индексов количественных и качественных показателей?

4. Какую роль играют «веса» при построении сводных индексов?

5. В каких случаях в статистическом анализе используется агрегатная форма индексов?

6. В чем заключается сущность средних индексов, как строятся и где используются эти индексы?

7. Каковы возможности использования индексов Пааше и Ласпейреса? В чем заключаются особенности их построения?

8. В чем отличие индексов переменного и постоянного состава? Для каких целей используются эти индексы? Как взаимосвязаны индексы переменного состава, постоянного состава и индекс структурных сдвигов?

9. Каковы методологические принципы построения территориальных индексов?

10. Какой вид индекса – Пааше или Ласпейреса - используется для расчета сводного индекса потребительских цен?

             11. Что представляет собой индекс цен – дефлятор ВВП?

Литература:[2], [5], [8], [10], [11], [12], [13], [14].

Интернет – ресурсы: [1], [2], [5], [6].

 

---

Дата добавления: 2018-06-01; просмотров: 436; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!