Алгоритм решения линейного однородного уравнения 2-го порядка с постоянными коэффициентами
- По заданному уравнению y''(x) + p*y'(x) + q*y(x) =0 составляется алгебраическое квадратное уравнение k2+p*k+q=0 и находятся его корни k1 и k2.
- Полученные значения k1 , k2 используются при построении формул для решения ДУ (1):
В зависимости от знака дискриминанта D = p2/4 - q и корней k1 , k2 имеется три случая:
1. D>0 (т.е. k1≠k2 - действительные неравные числа)
Имеются два линейно независимых решения: y1(x) = ek1x, y2(x) = ek2x
2. D=0 (т.е. k1=k2 - действительные равные числа)
Имеются два линейно независимых решения: y1(x)=ek1x, y2(x)=x*ek1x
3. D<0 (т.е. k1 ≠ k2 - комплексные неравные числа)
k1= a + i*b, k2= a - i*b, где a = -p/2, b = √|D|, i=√(-1)
Имеются два линейно независимых решения: y1(x)=eаxcos(b*x),
y2(x)= eаxsin(b*x)
Общее решение: у(х) = С1*y1(x)+С2* y2(x), где С1, С2 - произвольные константы.
Примеры.
1) D>0 
2) Решим уравнение 
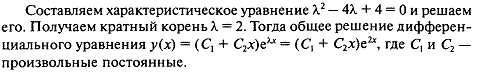
1a) k2+4k+13=0
k1= -4/2 + Ö(42/4-13)= -2 + Ö-9 = -2+√((-1)9)=-2+√(-1)√9)= -2+ i*3; k2= -2- i*3
a=-2, b=3
Ответ: y1(x)=exp(-2x)*cos(3*x), y2(x)=exp(-2x)*sin(3*x)
у = С1*exp(-2x)*cos(3*x) + С2*exp(-2x)*sin(3*x)
2) D < 0
4) 
Определение общего решения (общего интеграла):
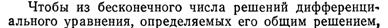
3) D < 0
Решение: 
4) D=0 
Упражнения (задачи с ответами)
Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
y'' + py' + qy = f(x) (1)
Например: y(x)'' + 3*y(x)' + 2*y(x) =xe2x
|
|
|
Общим решением дифференциального. уравнения 2-го порядка называется функция которая зависит от двух произвольных постоянных С1, С2 и удовлетворяет дифференциальному уравнению при любом конкретных значениях постоянных.
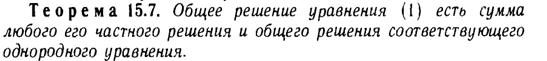
Отыскание частного решения дифференциального уравнения, удовлетворяющего начальным условиям вида: у=у0 при х=х0 и у'=у1 при х=х0, называется задачей Коши.
Теорема. Если в правой части уравнения (1) f(x)=f1(x)+f2(x),то частное решение (1) равно сумме частного решения уравнения с f1(x) и решения уравнения с f2(x).
* * *
Вид частного решения в зависимости от вида f(x) и корней характеристического уравнения.
0. Пусть f(x) = Pn(x), где Pn-многочлен n-й степени.
Pn(x)= a0*x0 +a1*x1+a2*x2+...+an*xn.
Например, P2(x)= a0*x0 +a1*x1+a2*x2.
Тогда:
1) Если ЧИСЛО 0 не равно ни одному из корней характеристического уравнения
k2+pk+q=0 (т.е. 0 ¹ k1 , 0 ¹ k2),
то решение имеет вид y*=Qn(x)-многочлен той же степени n.
Алгоритм решения. Неизвестные множители многочлена Qn(x) определяются следующим образом. Выписываем выражение для у* (например, у*= (ax+b), где a и b - неизвестные множители). Находим формулы для y*' и y*''. (В нашем примере у*'=a, y*''=0 ). Подставляем выражения для у*, y*' и y*'' в уравнение (1), приводим все соответствующие члены в правой и левой частях уравнения (например, -x+3x заменяем на 2х). Затем приравниваем множители при одинаковой степени x (x0,x1,x2,...,xn) в левой и правой части полученного тождества (например, если получено тождество (a+b)x+2b=3x-4, то оно равносильно системе двух уравнений: a+b=3 и 2b= - 4 ). Таким образом, мы получаем n+1 уравнений для определения n+1 неизвестных коэффициентов в многочлене Qn(x).
|
|
|
2) Если число 0 равно одному из неравных (при D>0)корней характеристического уравнения ( 0 = k1 , 0 ¹ k2), то решение имеет вид y*=x*Qn(x) (вводится дополнительный множитель х). Неизвестные множители многочлена Qn(x) определяются аналогично.
3) Если 0 является двукратным корнем характеристического уравнения (0 =k1=k2), то решение имеет вид y*=x2*Qn(x) (вводится дополнительный множитель х2).
Неизвестные множители многочлена Qn(x) определяются аналогично.
Следует подчеркнуть, что рассмотренный случай (f(x)=Pn(x)) является частным по отношению к случаю I., рассмотренному ниже.
I. Пусть f(x) = Pn(x)*exp(a*x), где Pn-многочлен n-й степени,exp(ax)= eax.
Pn(x)= a0*x0 +a1*x1+a2*x2+...+an*xn a - действительное число.
Тогда:
1) Если a не равно ни одному из корней характеристического уравнения
|
|
|
k2+pk+q=0 ( a ¹ k1 , a ¹ k2),
то решение имеет вид y*=Qn(x)exp(ax).
Неизвестные множители многочлена Qn(x) определяются следующим образом.
Выписываем выражение для у* (например, у*= (ax+b)e2x). Находим формулы для y*' и y*''.Подставляем выражения для у*, y*' и y*'' в уравнение (1), делим обе части получившегося уравнения на eαx , приводим все подобные члены в правой и левой частях уравнения. Затем приравниваем множители при одинаковой степени x (x0,x1,x2,...,xn) в левой и правой части полученного тождества. Таким образом, мы получаем n+1 уравнений для определения n+1 неизвестных коэффициентов в многочлене Qn(x).
2) Если a равно одному из неравных (при D>0) корней характеристического уравнения ( a = k1 , a ¹ k2), то решение имеет вид y*=x*Qn(x)exp(ax). Неизвестные множители многочлена Qn(x) определяются аналогично - (вводится дополнительный множитель х).
3) Если α является двукратным корнем характеристического уравнения (α =k1=k2), то решение имеет вид y*=x2*Qn(x)exp(α x) - (вводится дополнительный множитель х2).
Неизвестные множители многочлена Qn(x) определяются аналогично.
4) Рассмотренный выше случай f(x) = Pn(x) можно рассматривать как частный случай f(x)=Pn(x)*exp(a*x) при α=0 (т.к. exp(0)=1).
Мы можем полагать f(x)= Pn(x)*1= Pn(x)*exp(0*x), т.е. α=0 и , таким образом, сравнивать k1,k2 с нулем .
|
|
|
Пример.
В приведенном ниже примере 1 правая часть f(x) = x. Представляем ее в виде: x=x*1=x*e0*x. Таким образом, aв выражении Pn(x)*exp(ax) равно 0.Это значение aсравнивается с корнями k1,k2.
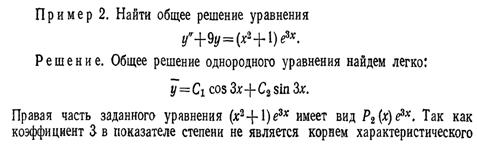
Пример.
Пример.
Решение: в правой части уравнения нет множителя exp(ax)(формально, он есть : exp(0*x)=1 с a = 0 ). Итак a =0 и (a ¹ k1 , a ¹ k2).
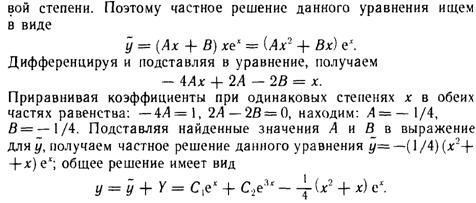
II. Правая часть уравнения содержит sin и cos
Пусть f(x) = P(x)*exp(ax)cos(bx) + Q(x)*exp(ax)sin(bx), где P, Q -
многочлены. Тогда:
1) Если комплексное число α + i*β не является корнем характеристического
уравнения( α + i*β ≠ k1 , α + i*β ≠ k2) , то частное решение следует искать в виде
y*= U(x)*exp(α x)cos(βx) + V(x)*exp(α x)sin(βx)
где U и V - многочлены, степень которых равна наивысшей степени многочленов P(x) и Q(x).
2) Если комплексное число α + iβ является корнем характеристического
уравнения ( α + iβ = k1) , то частное решение следует искать в виде
y*= x*U(x)*exp(α x)cos(βx) + x*V(x)*exp(α x)sin(βx)
Следует отметить, что даже если в правой части (1) присутствует только один член (например, нет слагаемого с sin(x)), то частное решение y* следует искать в указанном выше общем виде.
3) Частный случай.
Примеры для частного случая 3).
y''+y= sin(x)
k2+1=0 k1=i, k2= -i
В правой части
Примеры для общего случая 1),2):
1) y'' - y = 3e2xcos(x)
Степень многочлена в правой части равна нулю. k1=1, k2=-1.
Общее решение однородного уравнения: С1*ex + C2*e-x
Т.к. α + i*β =2+i*1 не является корнем характеристического уравнения, то
: y* = e2x(A*cos(x) + Bsin(x)).
Подставив это выражение в уравнение получим: (2A+4B)e2xcos(x) + (-4A+2B)e2xsin(x) = 3e2xcos(x)
Приравнивая коэффициенты при cos(x) (и sin(x)) в правой и левой частях,
получим: 22A+4B=3; -4A+2B=0. Получаем A=3/4, B=3/5.
Следовательно: y* = e2x*[3/10 cos(x) + 3/5sin(x)]
Общее решение: С1*ex + C2*e-x + e2x*[3/10 cos(x) + 3/5sin(x)]
2)
где 1-е слагаемое - решение однородного уравнения, а 2-е y* - решение неоднородного уравнения.
Упражнения.
Задачи с решениями
1) 
y(x) = 
2) 
Частное решение: 
3) 
Частное решение: 
Приложение
Ликбез по мат. анализу
I Функция
Определение: Переменная y называется функцией от переменной x (y=f(x)), если по некоторому правилу каждому значению х ставится в соответствие одно определенное значение y. (Читается: "y равен эф от икс"). Таким образом, правило f числу х сопоставляет число y. Число х называется значением аргумента функции, y –значением функции.
Переменная х называется независимой переменной, y - зависимой.
Способы задания функции: аналитический (формулой, например, y=x2), графиком, таблицей.
Предел функции
Это понятие лежит в основе математического анализа. Дадим пояснение.
Если значения переменной y приближаются к некоторому числу b (т.е., y - b стремится к 0) когда значения аргумента х приближаются к числу а, то число b называют пределом функции при стремлении х к а (говорят еще - в точке а).
Принято писать: lim f(x) = b
при x--> a
Пример: 1) Если y = x2, то: lim y = a2 при х → a
Действительно: у -а2 = х2-а2 = (х+а)*(х-а) --> 0, т.к. х-а --> 0 и х+а - ограничено.
2) lim(x2-1)/(x-1)=lim(x-1)(x+1)/(x-1)=lim(x+1)= lim(x)+ lim(1)=1+1=2 при х -->1.
2) Степенная функция у = ха
Логарифмическая функция y=loga(x) является обратной по отношению к показательной y=ax (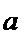 
alog(x) =x; loga(ax)=x ).
Логарифм loge(x) по основанию a=e=2,71... называется натуральным логарифмом и обозначается через ln(x).
Свойства логарифма: loga(b) + loga(c)=loga(b*c); loga(b) - loga(c)= loga(b/c);
Важное свойство: eln(b)=b
Свойства корней и степеней: √x = x1/2; 1/x=x-1; 1/x2=x-2; 1/√x= x-1/2;
√(x2)=| x| (где | x| - модуль числа х, |-3|=3).
ab*ac = ab+c; ab/ac = ab - c;
II Производная
Дата добавления: 2018-06-01; просмотров: 692; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!