Упражнения (задачи с ответами)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Оглавление
Дифференциальные уравнения с.1
Уравнения 1-го порядка с разделяющимися переменными с.1
Примеры на ДУ с раздел. переменными (с решениями). с.2
Упражнения (задачи с ответами): с.4
Однородные уравнения первого порядка с.4
Линейные дифференциальные уравнения первого порядка с.7
Линейные однородные ДУ второго порядка с постоянными коэффициентами с.10
Приложение. Функция, производная, интеграл, комплексные числа с. 21
I ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ1-го порядка
Дифференциальное уравнение (ДУ) первого порядка имеет вид: F(x,y,y')=0
Если его разрешить относительно производной, то оно примет вид: y'(x)=f(x,y(x)).
Например: y'(x)=x/y(x).
Общим решением дифференциального уравнения 1-го порядка называется функция y=φ(x,C) которая зависит от одной произвольной постоянной интегрирования С и удовлетворяет дифференциальному уравнению при любом конкретном значении постоянной C.
Например, для уравнения y'(x)=x/y(x) общим решением будет совокупность двух функций: y(x)= + √(x2+C) и y(x)= - √(x2+C).
Или: y(x)= ±√(x2+C).
|
|
|
Отыскание частного решения дифференциального уравнения, удовлетворяющего начальному условию вида: у=у0 при х=х0 (например, у(1)=2), называется задачей Коши.
Уравнения 1-го порядка с разделяющимися переменными
Подобное уравнение можно привести к виду: y'*f1(y)=f2(x). (1)
Таким образом, переменные у и х разделены — находятся по разные стороны знака равенства (у - слева, х - справа).
Следует подчеркнуть, что выражение y'(х)*f1(y(x)) является производной функции F1(y(x)), где F1(y)- первообразная функции f1(y). (Т.е., F1 '(у)=f1(у)) ).
На этом основано приведенное ниже решение уравнения (1).
Учтя, что y'(x)=dy/dx, уравнение (1) можно представить в виде: dy /dx*f1(y) =f2(x). Тогда, формально умножив обе части на dx, получим уравнение в форме:
f1(y)dy=f2(x)dx (2)
Алгоритм решения: Общий интеграл уравнения находится почленным интегрированием правой части равенства (2) по х: (∫f2(x)dx= F2(x)+С2 ), и левой части — интегрированием по у (∫ f1(y)dy =F1(у)+С1 ) и, затем, приравниванием результатов интегрирования:
F1(у)+С1 = F2(x)+С2 или F1(у(х)) = F2(x)+С
Данное уравнение уже не содержит производной y'(x). Остается только получить явную формулу для у(х): y =...
|
|
|
Суммируем алгоритм решения:
1) Если заданное уравнение записано с использованием у'(x) (например: y'*x=y+1), то:
- Оно приводится к виду: y'*f1(y)=f2(x).
- Затем составляется равенство: ∫f1(y)dy = ∫f2(x)dx + С.
- Находятся первообразные F1(у) для f1(y) и F2(x) для f2(x).
- Составляется уравнение: F1(у)= F2(x) +С.
- Последнее уравнение решается относительно у, т.е., находится формула у =...
2) Если заданное уравнение записано в виде φ1(...)dy+φ2()dx = 0 (например:
(х+1)3dy - (y-2)2dx=0), то:
- Приводим его к видуf1(y)dy=f2(x)dx.
- Составляем равенство: ∫f1(y)dy = ∫f2(x)dx + С и далее как в предыдущем пункте.
* * *
Ликбез по алгебре (действия, часто используемые при решении уравнений с разделяющимися переменными)
Перенос слагаемых и множителей из одной части уравнения в другую
1) Если a + b = c, то a = c - b (Вычитаем b из обеих частей исходного равенства: слева b сокращается, справа появляется со знаком минус).
(y'+1 = x --> y' = x -1 ).
Аналогично: если a = b + c, то a - b = c
2) Если a*b = c, то a = c / b (Делим обе части исходного равенства на b, слева b сокращается, справа появляется в знаменателе).
(y'*x =1 --> y' =1/ x ).
Если a / b = c, то a = c* b (Умножаем обе части на b, слева b сокращается, справа появляется в числителе).
|
|
|
Аналогично: если a = c/b, то a*b = c
Примеры на раздел. переменные (с решениями).
Примеры.
1) y'y=x+1 Уравнение уже имеет вид y'*f1(y)=f2(x). -->
Решение: ∫f1(y)dy = ∫f2(x)dx + С --> ∫ ydy = ∫ (x+1)dx --> ∫ydy = ∫ xdx +∫1dx --> y2/2+C1=x2/2+x+C2 --> y2/2=x2/2+x+C --> |y|=√(x2+2x+2C) -->
Ответ: y(x)=±√(x2+2x+C3)
2) То же уравнение y'y=x+1 можно записать в виде: ydy - (x+1)dx=0 -->
--> ydy = (x+1)dx --> ∫ ydy = ∫ (x+1)dx и т.д.
3) y'y2 = sin(2x) --> ∫ y2dy = ∫ sin(2x)dx --> y3/3 = - (1/2)cos(2x) + C -->
--> Ответ: y(x)= [- (3/2)cos(2x)+C]1/3
4) y'/y = x2 --> ∫ 1/ydy = ∫ x2dx --> ln|y| = x3/3+C --> |y|= e x3/3+C = e x3/3eC = e x3/3C 1
--> y = ± C 1 e x3/3 = C 2 e x3/3 --> Ответ: y = C 2 e x3/3
3)  --> Для приведения к виду y'*f1(y)=f2(x) делим на у: y' *(1/y) =1/x --> Умножаем на dx: (1/y)*dy =(1/x)*dx --> ∫(1/y)dy=∫(1/x)dx --> ln|y|=ln|x|+C1 (*)
--> Для приведения к виду y'*f1(y)=f2(x) делим на у: y' *(1/y) =1/x --> Умножаем на dx: (1/y)*dy =(1/x)*dx --> ∫(1/y)dy=∫(1/x)dx --> ln|y|=ln|x|+C1 (*)
Далее возможны два различных преобразования:
а) Полагаем в уравнении (*) С1=ln|C2| --> ln|y|=ln|x|+ ln|C2| -->
ln|y|=ln(|x*C2| Следовательно: |y|=|xC2|
Полагая С = ± |C2|, получим: у=Сх.
б) Итак: ln|y|=ln|x|+C1 (*) --> По свойству логарифма: |y|=eln|x|+C1 -->
Т.к. ab+c=ab*ac: |y|=eln|x|*eC1 --> Полагаем С3= eC1 : |y|=eln|x|*C3 -->
--->По свойству логарифма: eln|x| = |x| : |y|==C3|x| --> y=±C3x -->
Полагаем С=±C3 : Ответ: у=Сх.
|
|
|

2) x+y'=0 Решение: xdx +ydy=0 -->
Ответ: y=√ (С1-х2)1/2
3)
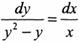


----->
 Представим C1 в виде логарифма новой константы С:
Представим C1 в виде логарифма новой константы С:
Отсюда ln|(y-1)/y|=ln(|x|*C) и (y-1)/y=xC.
Далее разрешаем уравнение относительно у: y-1= xCy; y*(1+xC)=1 и Ответ: y=1/(1+xC)
4) y'y2=x+1
Решение: ⟆y2dy =⟆(x+1)dx+С --> y3/3=x2/2+C --> Ответ: y=(3(x2/2 + C))1/3
5)


1/(y-2)= 1/(2(x+1)2)- C ---> Ответ: y=1/(1/(2(x+1)2)-C)+2
6)

при условии y(1)=3



Ответ: y(x)=±√(x3+x+9)
7) 
Решить уравнение и найти частное решение, удовлетворяющее условию y(1)=0,5




8) Решить уравнение 


* * *
Упражнения (задачи с ответами)
Проинтегрировать ДУ с разделяющимися переменными:
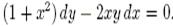 Ответ: у=С(1+х2)
Ответ: у=С(1+х2)
y'- xy2 = 2xy  Ответ: y=2/(ce-x2 - 1)
Ответ: y=2/(ce-x2 - 1)
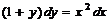 Ответ:общий интеграл имеет вид
Ответ:общий интеграл имеет вид 
ydx-xdy=0 Отв. y=Cx
(1+u)vdu+(1-v)udv=0 Отв. lnuv + u - v=C
(1+y)dx-(1-x)dy=0 Отв. (1+y)(1-x)=C
* * *
Дата добавления: 2018-06-01; просмотров: 551; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
