Вычисление второй производной
Численное дифференцирование применяется тогда, когда функцию трудно или невозможно продифференцировать аналитически. Например, необходимость в численном дифференцировании возникает в том случае, когда функция задана таблично. Кроме того, формулы численного дифференцирования широко используются при разработке вычислительных методов решения многих задач (решение дифференциальных уравнений, поиск решений нелинейных уравнений, поиск точек экстремум функци1 и др.)
Простейшие формулы численного дифференцирования
Предположим, что в окрестности точки х функция дифференцируема достаточное число раз. Исходя из определения производной
Естественно попытаться использовать для ее вычисления две простейшие приближенные формулы:
(1)
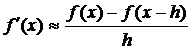, (2)
соответствующие выбору фиксированных значений 
Здесь h>0 - малый параметр (шаг). Разностные отношения в правых частях формул (1) и (2) часто называют правой и левой разностными производными.
Для оценки погрешностей
введенных формул численного дифференцирования (погрешностей аппроксимации) воспользуемся формулами Тейлора:
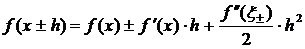(3)
Здесь и далее 
и 
- некоторые точки , расположенные на интервалах (x, x+h) и (x-h, x) соответственно.
Подставляя разложения (3) в выражения для 
, получаем
Следовательно,
Таким образом, формулы (1), (2) имеют первый порядок точности по h. Иначе говоря, правая и левая разностные производные аппроксимируют производную 
с первым порядком точности.
|
|
|
Приведенные формулы численного дифференцирования имеют простую геометрическую интерпретацию (рис.1). Пусть N0, N-, N+ - расположенные на графике функции y=f(x) точки с координатами (x, f(x)), (x-h, f(x-h)) и f(x, f(x+h)). Как известно, производная равна тангенсу угла α наклона к оси ОХ касательной, проведенной к графику функции в точке N0.
(ГРАФИКИ)
Формула (1) соответствует приближенной замене производной 
правой разностной производной 
, равно тангенсу угла 
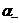секущей, проведенной через точки N0 и N- .
Естественно предположить, что лучшим по сравнению с 
и 
приближением к является тангенс угла наклона α0 секущей к графику, проведенной через точки N-, N+ (см. рис.2). Соответствующая приближенная формула имеет вид
(6)
Величину в правой части этой формулы часто называют центральной разностной производной.
Подставляя в выражение для погрешности
соответствующие разложения по формуле Тейлора
получаем 
.
Следовательно, справедлива оценка погрешности
(7)
Таким образом, центральная разностная производная аппроксимирует производную со вторым порядком точности относительно h.
|
|
|
Для вычисления можно получить формулы любого порядка точности. Однако в таких формулах с ростом порядка точности возрастает и число используемых значений функции. Например, формула 
(8)
имеет четвертый порядок точности.
Вычисление второй производной
Наиболее простой и широко применяемой для приближенного вычисления второй производной является следующая формула 
(9)
Величину в правой части этого приближенного равенства часто называют второй разностной производной.
Подставляя в выражение для погрешности 
соответствующие разложения по формуле Тейлора 
получаем 
Следовательно, 
(10)
Таким образом, формула (9) имеет второй порядок точности. Для вычисления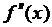 
можно получить формулы любого порядка точности. Например, формула 
(11) имеет четвертый порядок точности.
Дата добавления: 2018-06-27; просмотров: 376; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!