Отыскание интервалов выпуклости и точек перегиба
Достаточное условие выпуклости функции на интервале. Если вторая производная f"(х) существует на интервале (а, b) и не меняет знак на этом интервале, то:
1) при f"(х) > 0 (знак + ) функция f(х) выпукла вниз на интервале (а;b);
2) при f"(х) < 0 (знак - ) функция f(х) выпукла вверх на интервале (а;b).
Таким образом, для нахождения интервалов выпуклости вверх и выпуклости вниз функции нужно найти вторую производную и решить неравенства f"(х) < 0 и f"(х) > 0.
Точка М0(х0; f(х0)) графика функции у = f(х) называется точкой перегиба этого графика, если существует такая окрестность точки х0, в пределах которой график функции у = f(х) слева и справа от т. М0 имеет разные направления выпуклости.
На рис. 5 изображен график функции, имеющей перегиб в точке М0(х0; f(х0)).
Необходимый признак существования точки перегиба. Если функция в точке х0 имеет перегиб, то вторая производная в этой точке либо не существует, либо равна нулю.
Точки, в которых вторая производная обращается в нуль или не существует, называют критическими точками II-го рода. В этих точках перегиб может быть, а может и не быть. Этот вопрос решается с помощью следующего признака.
Достаточный признак существования точки перегиба. Пусть функция определена и непрерывна в некоторой окрестности точки х0, включая саму точку. Пусть, далее, вторая производная в этой точке равна нулю или не существует. Тогда, если f"(х) < 0 при х <х0 и f"(х) > 0 при х > х0 или f"(х) > 0 при х < х0 и f"(х) < 0 при х > х0, то М0(х0, (f(х0)) является точкой перегиба кривой у = f(х).
|
|
|
Дифференциал. Определение. Применение дифференциала к приближенным вычислениям
Дифференциал
Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.
Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).
Это записывается так:
или
или же
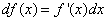
Применение дифференциала к приближенным вычислениям
Понятие дифференциала подсказывает, что если какой-Либо процесс по характеру своего изменения близок к линейному, то приращение функции мало отличается от дифференциала. Кроме того, если функция имеет конечную производную в некоторой точке х, то ее приращение и дифференциал также бесконечно малы при 
, стремящемся к нулю:
,
Так как дифференцируемая функция непрерывна,
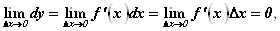
Потому что произведение ограниченной функции на бесконечно малую при DX, стремящемся к нулю, есть функция бесконечно малая.
Более того, эти две бесконечно малые функции при 
эквивалентны:
Эквивалентность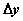 
и 
дает возможность при малых приращениях аргумента приближенно считать
|
|
|
Или
Что может дать эта формула? Пусть в некоторой точке 
сравнительно просто вычисляются значения 
и 
. Тогда в другой точке 
, отстоящей недалеко от , возможно представление :
(11. 16)
Здесь остается открытым вопрос о точности получаемого результата. Это обстоятельство снижает ценность данной формулы приближенного вычисления, но в основном она полезна и широко применяется на практике.
Рассмотрим пример. В прямоугольном треугольнике катеты a=5 м и b=12 м. Какой будет гипотенуза этого треугольника, если катет a уменьшить на 0,2 м (рис. 11.5, a)?
Найдем первоначальную длину гипотенузы:
.
После уменьшения катета a на 0,2 м гипотенуза будет равна (рис. 11.5, a)
Применим теперь формулу (11.16) для приближенного нахождения с в связи с уменьшением катета a, рассматривая функцию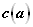 
вида:
(B=Const);
;
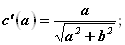
В обоих случаях мы получили приближенное значение искомой величины. Но в первом случае погрешность возникает в результате приближенных вычислений, а во втором, сравнительно более простом, – В связи с применением приближенной формулы (к ней также может добавиться погрешность, вызванная приближенными вычислениями). Отметим, что при уменьшении катета a На 0,2 м гипотенуза с уменьшилась примерно на 0,08 м, а полученные нами приближенные значения при этом отличаются лишь на 0,001 м.
|
|
|
Рассмотрим другую ситуацию: в этом же треугольнике уменьшим гипотенузу с на 0,2 м, оставив катет b без изменения (рис. 11.5, б). Определим, как в этом случае изменится катет A:
Дата добавления: 2018-05-13; просмотров: 368; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!