Скалярное, векторное и смешанное произведения векторов, их геометрический и физический смысл.
Скалярное произведение векторов
В векторной алгебре рассматриваются два вида произведения двух векторов: скалярное или векторное. Результатом скалярного умножения двух векторов является число (скаляр); результатом векторного умножения двух векторов является вектор.
Определение 1.Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла φ между векторами (рис.4.1).
Замечание 1. Скалярное умножение нельзя распространить на случай трех векторов-сомножителей, так как результатом его будет уже вектор, а не число.
Рис. 4.1. К понятию скалярного произведения
Для обозначения скалярного произведения вектора 
на вектор 
упот-ребляется одна из записей : 
.Согласно определению имеем 
(1)Заметив, что согласно рис. 3.1 
,равенство (1) можно записать в виде
или 
.
Таким образом, скалярное произведение двух векторов равно длине одного вектора, умноженной на проекцию второго на направление первого.
Итак, в результате скалярного произведения получается число (скаляр), а не новый вектор .
Физический смысл скалярного произведения заключается в том, что скалярное произведение 
численно равно работе А силы 
по направленному отрезку 
.
Геометрический смысл скалярного произведения: скалярное произведение вектора на единичный вектор 
равно проекции вектора 
на направление, определяемое , т. е. 
.
|
|
|
Из определения скалярного произведения вытекает следующая таблица умножения ортов 
:
.
Если векторы заданы своими координатами 
и 
, т. е. 
, 
, то, перемножая эти векторы скалярно и используя таблицу умножения ортов, получим выражение скалярного произведения 
через координаты векторов:
.
Векторное произведение двух векторов
Определение 1.Векторным произведением двух неколлинеарных век-торов 
и 
называется такой вектор 
который удовлетворяет трем условиям (рис.4.4).
Имеет модуль
1) 
; (9)
2) 
т.е. перпендикулярен к плоскости векторов 
и ;
3) направлен так, чтобы тройка векторов , , бы-ла правой.
Обозначение : = × или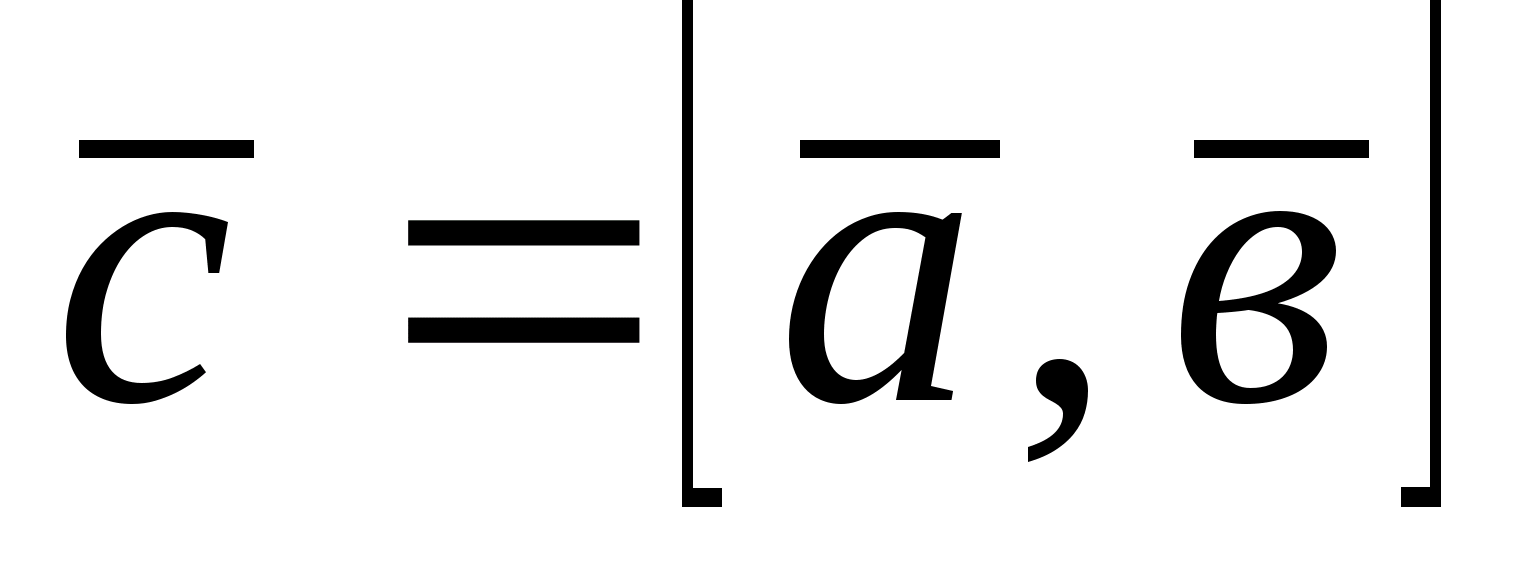 
Рис.4.4. К понятию векторного произведения.
Замечание.
1. Приведенные условия однозначно определяют векторное произведение, если сомножители – ненулевые векторы. Если хоть один из сомножителей – нулевой вектор, то векторное произведение равно нулю.
2. Модуль векторного произведения численно равен площади парал-лелограмма (рис. 4.4), построенного на векторах и .
Геометрический смысл векторного произведения заключается в том, что модуль векторного произведения двух векторов есть площадь параллелограмма, построенного на этих векторах;
|
|
|
Физический смысл векторного произведения
― момент силы 
относительно точки О; 
― радиус ― вектор точки приложения силы, тогда
,
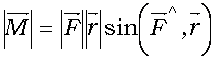причем, если перенести в точку О, то тройка , 
, должна быть ориентирована как вектора базиса.
Смешанное произведение
Смешанным (векторно-скалярным) произведением векторов 
называется число, которое получается в результате умножения векторного произведения 
скалярно на вектор и обозначаемое через 
.
Согласно определению = 
.
Геометрический смысл смешанного произведения. Модуль смешанного произведения трех векторов a, b и с равен объёму параллелепипеда, образованного этими векторами:
Vпарал = a · [b × c]
Геометрический смысл смешанного произведения. Объем пирамиды образованной тремя векторами a, b и с равен одной шестой части от модуля смешанного произведения этих векторов: Vпир = 1/6|a · [b × c
Плоскость в пространстве
Если поместить плоскость, на которой изображены точки и прямые, в трехмерное пространство, то мы получим точки и прямые в пространстве. Представление о плоскости в пространстве позволяет получить, к примеру, поверхность стола или стены. Однако, стол или стена имеют конечные размеры, а плоскость простирается за их границы в бесконечность.
|
|
|
Точки и прямые в пространстве обозначаются также как и на плоскости – большими и маленькими латинскими буквами соответственно. Например, точки А и Q, прямые а и d. Если заданы две точки, лежащие на прямой, то прямую можно обозначить двумя буквами, соответствующими этим точкам. К примеру, прямая АВ или ВА проходит через точки А и В. Плоскости принято обозначать маленькими греческими буквами, например, плоскости 
, 
или 
.
При решении задач возникает необходимость изображать плоскости на чертеже. Плоскость обычно изображают в виде параллелограмма или произвольной простой замкнутой области.
Плоскость обычно рассматривается вместе с точками, прямыми или другими плоскостями, при этом возникают различные варианты их взаимного расположения.
Прямая в пространстве.
Мысленно отмечаем две точки в пространстве и проводим с помощью линейки линию от одной точки до другой и за пределы точек в бесконечность.
Все обозначения точек, прямых и отрезков в пространстве аналогичны случаю на плоскости.
Вообще, прямая линия целиком принадлежит некоторой плоскости в пространстве. Это утверждение вытекает из аксиом:
|
|
|
через две точки проходит единственная прямая;
если две точки прямой лежат в некоторой плоскости, то все точки прямой лежат в этой плоскости.
Существует еще одна аксиома, которая позволяет рассматривать прямую в пространстве как пересечение двух плоскостей: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Дата добавления: 2018-05-13; просмотров: 6417; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!