Перехідна та імпульсна перехідна функції лінійних систем керування.
Нехай математична модель керування задана рівнянням n – ого порядку
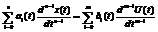 (1) .
(1) .
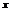 – одновимірний сигнал (функція), яка має багато похідних.
– одновимірний сигнал (функція), яка має багато похідних. 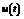 – подається на вхід системи.
– подається на вхід системи. 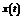 – реакція системи на
– реакція системи на 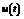 .
.
Розглянемо таку одиничну функцію:
 (2).
(2).
Озн.: Реакція системи (1) на вхідний сигнал (2) називається перехідною функцією системи, якщо до моменту подачі вхідного сигналу система знаходилась у стані спокою. Позначається 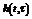 .
.
Перехідна функція – це розв’язок такої задачі: (3)-(4): 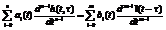 (3).
(3). 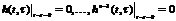 (4).
(4).
Озн.: імпульсною перехідною функцією  системи (1) називається реакція системи на вхідний сигнал типу одиничного імпульсу, якщо до моменту подачі вхідного сигналу система знаходилась в стані спокою.
системи (1) називається реакція системи на вхідний сигнал типу одиничного імпульсу, якщо до моменту подачі вхідного сигналу система знаходилась в стані спокою.  є розв’язком задачі (5)-(6):
є розв’язком задачі (5)-(6): 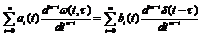 (5)
(5) 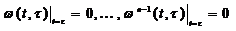 (6)
(6)
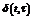 –ф-ія Дірака
–ф-ія Дірака 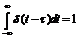 ,
, 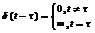 (7)
(7)
Властивості ф-ї. Дірака:
 (8)
(8) 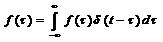 (9)
(9) 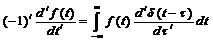 (10).
(10).
δможна подати у вигляді 2х вхідних сигналів, що мають протилежніінтенсивності,тоді 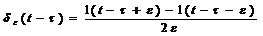
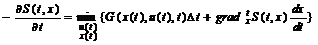 – рівняння Беллмана в диференціальній формі.
– рівняння Беллмана в диференціальній формі. 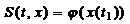 – крайова умова (записується із вигляду ф-ції S(t,x):
– крайова умова (записується із вигляду ф-ції S(t,x):  .
.
Зв’язок між вхідним і вихідним сигналами лінійної одновимірної системи керування
Розглянемо одновимірну лінійну систему зі змінними параметрами, яка описується рівнянням
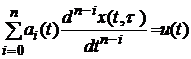 . (2.1)
. (2.1)
Нехай система до моменту подачі вхідного сигналу знаходиться в стані спокою. За початок відліку часу виберемо момент подачі вхідного сигналу і початкові умови запишемо у вигляді
|
|
|
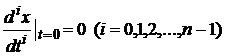 . (2.2)
. (2.2)
Знайдемо інтегральний зв’язок між вхідним 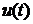 і вихідним
і вихідним 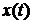 сигналами системи (2.1) за умови (2.2).
сигналами системи (2.1) за умови (2.2).
Нехай 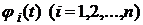 лінійно-незалежні розв’язки однорідного рівняння
лінійно-незалежні розв’язки однорідного рівняння
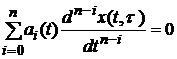 . (2.3)
. (2.3)
З теорії диференціальних рівнянь відомо, що розв’язок неоднорідного рівняння (2.1) за умови (2.2) можна подати у вигляді
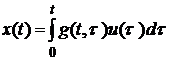 , (2.4)
, (2.4)
де
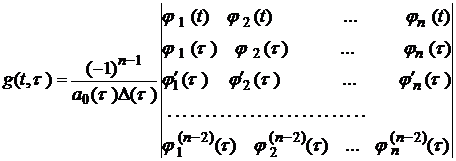 , (2.5)
, (2.5)
а
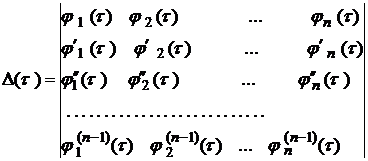 .
.
Перетворення Лапласа. Передавальна функція лінійної стаціонарної одновимірної системи керування
Основний зміст інтегральних перетворень, в тому числі й перетворення Лапласа, – це взаємно-однозначний перехід від одного класу функцій (функцій 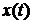 – класу оригіналів) до іншого класу функцій (наприклад, до
– класу оригіналів) до іншого класу функцій (наприклад, до 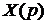 , який називається класом зображень). Уновому класі суттєво змінюється природа математичних операцій. А саме, інтегрування диференціального рівняння в класі оригіналів може звестися до відшукання коренів алгебраїчного рівняння в класі зображень. Такий перехід забезпечує спрощення відшукання розв’язку початкової задачі.
, який називається класом зображень). Уновому класі суттєво змінюється природа математичних операцій. А саме, інтегрування диференціального рівняння в класі оригіналів може звестися до відшукання коренів алгебраїчного рівняння в класі зображень. Такий перехід забезпечує спрощення відшукання розв’язку початкової задачі.
Означення 3.1Оригіналом (за Лапласом) називається функція 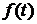 (нас цікавитимуть тільки дійсні функції) дійсного аргументу
(нас цікавитимуть тільки дійсні функції) дійсного аргументу 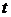 , яка задовольняє умови:
, яка задовольняє умови:
|
|
|
1) 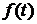 – однозначна неперервна або кусково-неперервна функція разом зі своїми похідними до
– однозначна неперервна або кусково-неперервна функція разом зі своїми похідними до 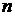 -го порядку на всій числовій осі
-го порядку на всій числовій осі 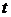 ;
;
2) 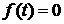 при
при 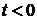 ;
;
3) існують такі числа 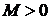 і
і 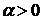 , що для
, що для 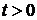
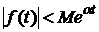
(точна нижня межа 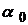 чисел
чисел 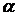 називається показником росту функції
називається показником росту функції 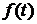 ).
).
Означення 3.2 (зображення за Лапласом). Зображенням функції-оригінала 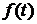 називається функція
називається функція 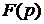 комплексної змінної
комплексної змінної 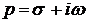 , яка визначається за допомогою інтеграла Лапласа
, яка визначається за допомогою інтеграла Лапласа
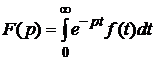 . (3.1)
. (3.1)
Наведемо без доведення наступні теореми.
Теорема 3.1 Якщо функція 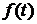 – оригінал з показником росту
– оригінал з показником росту 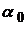 , то інтеграл
, то інтеграл 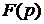 збігається в півплощині
збігається в півплощині  , в цій півплощині інтеграл є аналітичною функцією і в цій області
, в цій півплощині інтеграл є аналітичною функцією і в цій області  .
.
Теорема 3.2 Якщо функція 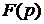 аналітична в області
аналітична в області  , у цій області
, у цій області  і інтеграл
і інтеграл 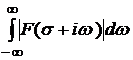 збігається, то функція
збігається, то функція 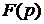 є зображенням, а її оригінал можна знайти за формулою
є зображенням, а її оригінал можна знайти за формулою
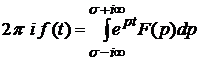 , (3.2)
, (3.2)
де інтегрування проводиться вздовж прямої, яка паралельна до уявної осі, на віддалі 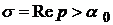 від неї.
від неї.
Розглянемо тепер лінійну систему керування зі сталими коефіцієнтами, яка описується рівнянням
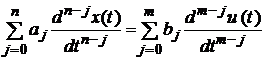 (3.3)
(3.3)
і до моменту 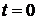 подачі сигналу керування ця система знаходиться в спокої, тобто
подачі сигналу керування ця система знаходиться в спокої, тобто
|
|
|
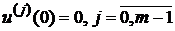 ,
,  . (3.4)
. (3.4)
Припустимо, що функції 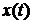 і
і 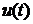 задовольняють умови оригінала. Застосуємо до рівняння (3.3) перетворення Лапласа (3.1). Враховуючи умови (3.4), знайдемо
задовольняють умови оригінала. Застосуємо до рівняння (3.3) перетворення Лапласа (3.1). Враховуючи умови (3.4), знайдемо
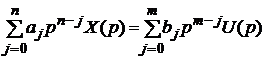 , (3.5)
, (3.5)
де
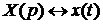 ,
, 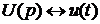 .
.
Запровадимо позначення
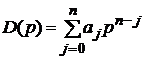 ,
, 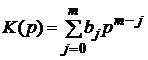 ,
,
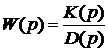 . (3.6)
. (3.6)
Тоді рівність (3.5) можна записати у вигляді
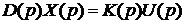 ,(3.7)
,(3.7)
Або 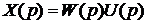 . (3.8)
. (3.8)
Функція 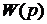 називається передавальною функцією системи.
називається передавальною функцією системи.
Дата добавления: 2018-05-13; просмотров: 393; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
