Аксиоматическое определение вероятности.
Необходимость формально логического обоснования теории вероятностей, её аксиоматического построения возникла в связи с развитием самой теории вероятностей как математической науки и её приложений в различных областях.
Впервые идея аксиоматического построения вероятностей была высказана российским академиком Бернштейном (Бернштейн Сергей Натанович 1880-1968), исходившим из качественного сравнения событий по их большей или меньшей вероятности.
В начале 30-х годов прошлого столетия академик Колмогоров (Колмогоров Андрей Николаевич 1903-1987) разработал иной подход, связывающий теорию вероятностей с современной метрической теорией функций и теорией множеств.
Приведём систему аксиом, предложенную Колмогоровым.
Аксиоматическое определение.
Вероятностью события А называется число Р(А), которое сопоставляется каждому событию рассматриваемого множества событий и которое удовлетворяет следующим аксиомам:
Аксиома 1: (неотрицательности) Вероятность любого события неотрицательна.
Аксиома 2: (нормировки) Вероятность достоверного события равна 1.
Аксиома 3: (сложения) Вероятность суммы любого конечного множества попарно несовместных событий равна сумме их вероятностей.
Аксиома 4: (однозначности) Эквивалентные события имеют равные вероятности.
Следствия из аксиом:
1. Вероятность невозможного события равна 0.
2. Вероятность события противоположного событию А

3. Вероятность любого события 
Аксиомы теории вероятностей позволяют вычислить вероятности любых событий через вероятности элементарных событий.
Вопрос о том, откуда берутся вероятности элементарных событий, при аксиоматическом построении теории вероятностей не рассматривается. На практике они определяются с помощью классического, статистического, геометрического определений.
Таким образом, аксиоматическое определение:
· Обобщает классическое, статистическое, геометрическое определения.
· Постулирует существование вероятности как объективно существующей характеристики реальных событий, не зависящей ни от самого исследователя, ни от количества проведённых им экспериментов.
Теоремы сложения и умножения вероятностей.
Как правило, для определения вероятностей событий применяются не непосредственные прямые методы, а косвенные, позволяющие по известным вероятностям одних событий определять вероятности других событий, с ними связанных. Применяя косвенные методы, мы всегда в той или иной форме пользуемся основными теоремами теории вероятностей – теоремами сложения и умножения вероятностей. Эти теоремы могут быть доказаны только для событий, сводящихся к схеме случаев. Для остальных событий они принимаются аксиоматически.
Теорема сложения вероятностей.
Вероятность суммы двух любых событий равна сумме вероятностей этих событий без вероятности их произведения:
Р(А+В)=Р(А)+Р(В)-Р(АВ)
(доказательство самостоятельно)
Следствия: 1. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:  .
.
2. Сумма вероятностей событий, образующих полную группу, равна 1.
Частный случай:  .
.
3. В случае суммы трёх и более событий проще перейти к противоположному событию: 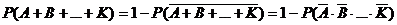
Пример: В колоде 36 карт. Объявлен козырь. Какова вероятность того, что вынутая наудачу карта будет козырем или тузом?
Решение: Пусть событие А – вынутая карта козырь, событие В – вынутая карта туз.
Тогда Р(А+В)=Р(А)+Р(В)-Р(АВ)= 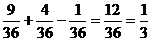 .
.
Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.
Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Пример: В урне 2 белых и 1 чёрный шар. Вынимают два шара. ассматриваются события: А – появление первого белого шара, В – появление второго белого шара. Вероятность события В если известно, что первый шар возвращается в урну, равна -  , если известно, что не возвращается, становится равной
, если известно, что не возвращается, становится равной  . Следовательно, В зависит от А.
. Следовательно, В зависит от А.
Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается
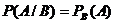
Условие независимости события А от события В: 
Теорема умножения вероятностей.
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие имело место:

(доказательство самостоятельно)
Следствия: 1. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:  .
.
2. Обобщим теорему на случай конечного числа событий.
Вероятность произведения конечного числа событий равна произведению вероятностей этих событий, причём вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место:

Пример: В урне 2 белых и 3 чёрных шара. Из урны вынимают подряд 2 шара. Найти вероятность того, что оба шара белые.
Решение: А1 - появление белого шара при первом вынимании,
А2 - появление белого шара при втором вынимании,
А - появление двух белых шаров.
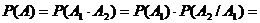
а) шар не возвращается в урну:  ;
;
б) шар возвращается в урну: 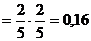 .
.
Дата добавления: 2018-05-13; просмотров: 7593; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
