Статистическое определение вероятности.
Статистической вероятностью события А называется относительная частота появления этого события в произведённых испытаниях:

где  – вероятность появления события А;
– вероятность появления события А;
 – относительная частота появления события А;
– относительная частота появления события А;
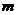 - число испытаний, в которых появилось событие А;
- число испытаний, в которых появилось событие А;
 - общее число испытаний.
- общее число испытаний.
В отличие от классической вероятности статистическая вероятность является характеристикой опытной, экспериментальной.
Пример: Для контроля качества изделий из партии наугад выбрано 100 изделий, среди которых 3 изделия оказались бракованными. Определить вероятность брака.
 .
.
Статистический способ определения вероятности применим лишь к тем событиям, которые обладают следующими свойствами:
· Рассматриваемые события должны быть исходами только тех испытаний, которые могут быть воспроизведены неограниченное число раз при одном и том же комплексе условий.
· События должны обладать статистической устойчивостью (или устойчи- востью относительных частот). Это означает, что в различных сериях испытаний относительная частота события изменяется незначительно.
· Число испытаний, в результате которых появляется событие А, должно быть достаточно велико.
Таким образом, статистическое определение вероятности хотя и достаточно полно выявляет содержание этого понятия, но не даёт возможности фактического вычисления вероятности, то есть не является рабочим определением.
Легко проверить, что свойства вероятности, вытекающие из классического определения, сохраняются и при статистическом определении вероятности.
Геометрическое определение вероятности.
На практике очень часто встречаются такие испытания, число возможных исходов которых бесконечно.
Иногда в таких случаях можно воспользоваться методом вычисления вероятности, в котором по-прежнему основную роль играет понятие равновозможности некоторых событий. Применяется этот метод в задачах, сводящихся к случайному бросанию точки на конечный участок прямой, плоскости, пространства. Отсюда и возникает само название вероятности – геометрическая вероятность.
Геометрической вероятностью события А называется отношение меры области, благоприятствующей появлению события А, к мере всей области.
Для определения ограничимся двумерным случаем. Одномерный и трёхмерный случаи отличаются только тем, что вместо площади в них нужно говорить о длинах и объёмах.
Пусть на плоскости имеется некоторая область  ,
,
площадь которой  , и в ней содержится другая
, и в ней содержится другая
область  , площадь которой
, площадь которой  . В область
. В область 
наудачу бросается точка. Спрашивается, чему равна вероятность того, что точка попадёт в область  ?
?
При этом предполагается, что наудачу брошенная точка может попасть в любую часть области  , и вероятность попасть в какую-либо часть области
, и вероятность попасть в какую-либо часть области  пропорциональна площади этой части и не зависит от её расположения и формы. Таким образом, вероятность попадания в область
пропорциональна площади этой части и не зависит от её расположения и формы. Таким образом, вероятность попадания в область  при бросании наудачу точки в область
при бросании наудачу точки в область  :
:

Пример: (задача о встрече) Два лица условились встретиться в определённом месте, договорившись только о том, что каждый является туда в любой момент времени между 11 и 12 часами и ждёт в течение 30 минут. Если партнёр к этому времени ещё не пришёл, или уже успел покинуть установленное место, встреча не состоится. Найти вероятность того, что встреча состоится.
Решение: Пусть х и у – моменты прихода в определённое место двух лиц.
Тогда  ,
, 


Встреча произойдёт, если  :
:
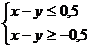



Замечание: Свойства вероятности сохраняются и при геометрическом определении вероятности.
Дата добавления: 2018-05-13; просмотров: 416; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
