Классическое определение вероятности.
Классический способ определения вероятности основан на понятии равновозможных и несовместных событий, которые являются исходами данного опыта и образуют полную группу несовместных событий.
Наиболее простым примером равновозможных и несовместных событий, образующих полную группу, является появление того или иного шара из урны, содержащей несколько одинаковых по размеру, весу и другим осязаемым признакам шаров, отличающихся лишь цветом, тщательно перемешанных перед выниманием.
Поэтому об испытании, исходы которого образуют полную группу несовместных и равновозможных событий, говорят, что оно сводится к схеме урн, или схеме случаев, или укладывается в классическую схему.
Равновозможные и несовместные события, составляющие полную группу, будем называть просто случаями или шансами. При этом в каждом опыте наряду со случаями могут происходить и более сложные события.
Пример: При подбрасывании игральной кости наряду со случаями Аi - выпадение i- очков на верхней грани можно рассматривать такие события, как В - выпадение чётного числа очков, С - выпадение числа очков, кратных трём …
По отношению к каждому событию, которое может произойти при осуществлении эксперимента, случаи делятся на благоприятствующие, при которых это событие происходит, и неблагоприятствующие, при которых событие не происходит. В предыдущем примере, событию В благоприятствуют случаи А2, А4, А6; событию С – случаи А3, А6.
|
|
|
Классической вероятностью появления некоторого события называется отношение числа случаев, благоприятствующих появлению этого события, к общему числу случаев равновозможных, несовместных, составляющих полную группу в данном опыте:
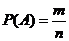
где Р(А) – вероятность появления события А; m - число случаев, благоприятствующих событию А; n - общее число случаев.
Примеры:
1) (смотри пример выше) Р(В)=  , Р(С)=
, Р(С)=  .
.
2) В урне находятся 9 красных и 6 синих шаров. Найти вероятность того, что вынутые наугад один, два шара окажутся красными.
А - вынутый наугад шар красный:
m=9, n=9+6=15, P(A)= 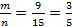
B - вынутые наугад два шара красные:

Из классического определения вероятности вытекают следующие свойства (показать самостоятельно):
1) Вероятность невозможного события равна 0;
2) Вероятность достоверного события равна 1;
3) Вероятность любого события заключена между 0 и 1;
4) Вероятность события, противоположного событию А,

Классическое определение вероятности предполагает, что число исходов испытания конечно. На практике же весьма часто встречаются испытания, число возможных случаев которых бесконечно. Кроме того, слабая сторона классического определения состоит в том, что очень часто невозможно представить результат испытания в виде совокупности элементарных событий. Ещё труднее указать основания, позволяющие считать элементарные исходы испытания равновозможными. Обычно о равновозможности элементарных исходов испытания заключают из соображений симметрии. Однако такие задачи на практике встречаются весьма редко. По этим причинам наряду с классическим определением вероятности пользуются и другими определениями вероятности.
|
|
|
Дата добавления: 2018-05-13; просмотров: 326; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
