Основные свойства неопределённого интеграла
1. Дифференциал от неопределённого интеграла равен подынтегральному выражению.

2. Производная неопределённого интеграла равна подынтегральной функции.

3. Неопределённый интеграл от производной некоторой функции равен этой функции, сложенной с некоторой произвольной постоянной.

4. Постоянный множитель можно выносить за знак неопределённого интеграла.
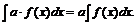
5. Неопределённый интеграл алгебраической суммы равен алгебраической сумме интегралов слагаемых.
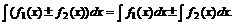
Таблица интегралов
1.  .
.
2. 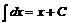 .
.
3. 
4. 
5. 
6. 
7. 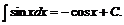
8. 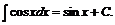
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
Метод непосредственного интегрирования
Этот метод интегрирования опирается на таблицу основных интегралов и простейшие правила интегрирования.
Пример 1. Вычислить интеграл  .
.
Разделим почленно числитель подынтегральной функции на знаменатель. Применяя свойства интегралов и таблицу интегралов, получим:

 .
.
Пример 2. Вычислить интеграл  .
.
Возводим числитель в куб и делим почленно на знаменатель. Имеем:

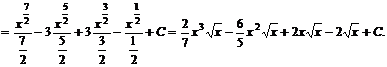
Пример 3. Вычислить интеграл  .
.
Освободившись от иррациональности в знаменателе, получим:


Пример 4. Вычислить интеграл  .
.
Запишем единицу, стоящую в числителе, как тригонометрическую. Разделив почленно числитель на знаменатель, получим:
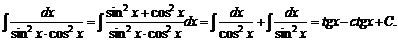
Метод интегрирования по частям
Метод интегрирования по частям основан на формуле
 (1)
(1)
которая называется формулой интегрирования по частям.
|
|
|
Применяя этот метод, мы должны вначале представить подынтегральное выражение в виде произведения одной функции на дифференциал другой функции. Пользуясь формулой (1), надо следить, чтобы подынтегральное выражение  было не сложнее, чем подынтегральное выражение
было не сложнее, чем подынтегральное выражение  .
.
При вычислении можно пользоваться следующими практическими советами. Если подынтегральное выражение представляет собой произведение либо тригонометрической функции на многочлен, либо показательной на многочлен, то за  следует принимать этот многочлен.
следует принимать этот многочлен.
Если в подынтегральное выражение входит множителем либо одна из обратных тригонометрических функций, либо функция 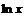 , то за
, то за 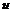 следует выбрать одну из указанных функций.
следует выбрать одну из указанных функций.
Пример 1. Вычислить интеграл  .
.
Положим,

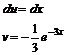
Используя формулу (1), получим
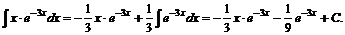
Пример 2. Вычислить интеграл  .
.
Пусть


Имеем:
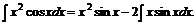
Полученный интеграл ещё раз интегрируем по частям:


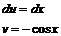

Окончательно получим:

Пример 3. Вычислить интеграл
 .
.
Интегрируем по частям:

 ,
,
 .
.
Мы получили интеграл той же сложности, что и исходный. Проинтегрируем его ещё раз по частям:
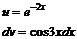
 ,
,
 .
.
Отсюда получим
 .
.
Перенесём интеграл из правой части равенства в левую и найдём его как из уравнения:
|
|
|


Метод замены переменной (метод подстановки)
Метод замены переменной является одним из основных методов интегрирования.
Пример 1. Вычислить интеграл 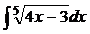 .
.
Выполним подстановку  , тогда
, тогда  , откуда
, откуда  .
.
Заданный интеграл преобразуется теперь к табличному
 .
.
Возвращаясь к первоначальной переменной  , получим
, получим

Пример 2. Вычислите интеграл  .
.
Сделаем подстановку  , тогда
, тогда  .
.
Интеграл примет вид
 .
.
При решении этой задачи можно рассуждать иначе. Введём множитель  под знак дифференциала, тогда получим
под знак дифференциала, тогда получим
 .
.
Пример 3. Вычислить интеграл 
Запишем интеграл в виде 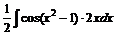 , тогда удобно сделать замену
, тогда удобно сделать замену  ,
,  .
.
Интеграл примет вид
 .
.
Замечание 1.
Пусть  , тогда
, тогда
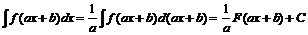 .
.
Будем использовать этот результат в дальнейших вычислениях
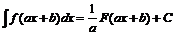 .
.
Например:
 .
.
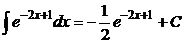 .
.
Замечание 2.
Если подынтегральное выражение содержит 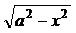 , то удобно применить подстановку
, то удобно применить подстановку  или подстановку
или подстановку 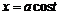 .
.
Если подынтегральное выражение содержит  , то удобно применить подстановку
, то удобно применить подстановку  или подстановку
или подстановку  .
.
Если подынтегральное выражение содержит  , то удобно применить подстановку
, то удобно применить подстановку  или подстановку
или подстановку  .
.
Пример 4. Вычислить интеграл  .
.
Так как под интегралом есть радикал 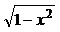 , то сделаем подстановку
, то сделаем подстановку  ; откуда
; откуда  .
.
|
|
|
Имеем:
 .
.

 .
.
Рассмотрим одно из определений определённого интеграла.
Пусть функция  задана на отрезке
задана на отрезке  и имеет на нём первообразную
и имеет на нём первообразную  .
.
Определение. Разность  называют определённым интегралом функции
называют определённым интегралом функции  по отрезку
по отрезку  и обозначают
и обозначают
 . (1)
. (1)
Здесь  называют нижним пределом интегрирования,
называют нижним пределом интегрирования,  — верхним пределом.
— верхним пределом.
Функция  , стоящая под знаком интеграла, предполагается непрерывной на
, стоящая под знаком интеграла, предполагается непрерывной на  .
.
Формулу (1) можно записать в виде:
 . (1¢)
. (1¢)
Формула (1¢) называется формулой Ньютона — Лейбница. Она устанавливает связь между неопределённым и определённым интегралами.
Определённый интеграл есть число. Числовое значение определённого интеграла зависит от вида функции  , стоящей под знаком интеграла, и от значений верхнего и нижнего пределов интегрирования.
, стоящей под знаком интеграла, и от значений верхнего и нижнего пределов интегрирования.
Пример 1. Вычислить  .
.
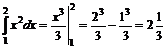 .
.
При вычислении определённого интеграла удобно пользоваться следующим правилом:
Сначала находят неопределённый интеграл данной функции.
Затем берётся функциональная часть неопределённого интеграла, то есть 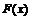 , и в неё вместо
, и в неё вместо  подставляется сначала верхний предел
подставляется сначала верхний предел  , потом нижний
, потом нижний  и из первого результата подстановки вычитается второй.
и из первого результата подстановки вычитается второй.
Пример 2. Вычислить 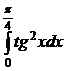 .
.
Находим неопределённый интеграл
|
|
|
 .
.
Далее по формуле (1) имеем:
 .
.
Основными методами вычисления определённого интеграла являются метод подстановки (замены переменной) и метод интегрирования по частям, известные по изучению неопределённого интеграла.
А) Метод подстановки
Сущность метода состоит в замене переменной интегрирования другой переменной, связанной с ней какими-либо функциональными соотношениями.
При использовании этого метода для вычисления неопределённых интегралов по окончании операции надо было возвращаться снова к первоначальной переменной, что вызывало иногда довольно большие трудности. Здесь такое возвращение не обязательно и заменяется изменением пределов интегрирования по новой переменной.
Пример 3. Вычислить интеграл  .
.
Введём новую переменную  , положив
, положив  (вспомни интегрирование иррациональных функций). Тогда
(вспомни интегрирование иррациональных функций). Тогда  .
.
Найдём пределы интегрирования для новой переменной  :
:

Заменяя переменную в определённом интеграле, получим:

Пример 4. Вычислить интеграл  .
.
Воспользуемся заменой переменной:
 , тогда
, тогда  .
.
Если 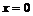 , то
, то 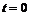 , если
, если 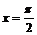 , то
, то  .
.
Выполняя замену, получаем
 .
.
Дата добавления: 2018-05-12; просмотров: 426; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
