НАКЛОННОЕ ПАДЕНИЕ ПЛОСКОЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ НА ГРАНИЦУ РАЗДЕЛА СРЕД

Стр 1 из 3Следующая ⇒

Лекция № 11.

Волновые явления на границе раздела двух сред

Учебные вопросы лекции:

Нормальное падение плоской электромагнитной волны на границу раздела сред.

Наклонное падение плоской электромагнитной волны на границу раздела сред.

Отражение и преломление плоских электромагнитных волн границе диэлектрик–диэлектрик.

Отражение и преломление плоских электромагнитных волн границе диэлектрик–проводник. Скин-эффект.

Введение

Плоские электромагнитные волны, рассматриваемые как предельный случай сферических волн, изучались нами как волны, возбуждаемые и распространяющиеся в неограниченной однородной среде. Однако в большинстве практических задач нельзя говорить о бесконечном однородном пространстве. Так волны, распространяющиеся над Землей, следует изучать с учетом их поведения на границе земля–воздух; характер волн в линиях передачи существенно зависит от направляющих плоскостей, ограничивающих линию передачи и т.д.

Целью данной лекции является изучение основных особенностей распространения электромагнитных волн в пространстве, состоящем из разнородных областей.

НОРМАЛЬНОЕ ПАДЕНИЕ ПЛОСКОЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ НА ГРАНИЦУ РАЗДЕЛА СРЕД

В первом вопросе лекции рассматриваются волновые явления на границе раздела сред при нормальном падении плоской волны, вводятся понятия коэффициента отражения и передачи.

Пусть плоскость хОy, как показано на рис. 1, разделяет две среды, диэлектрическая и магнитная проницаемость которых соответственно равны: e_а1, m_а1 при координате z < 0; и e_а2, m_а2 при z > 0.

Для простоты потери в обеих средах учитывать не будем, т.е. полагаем, что s₁ = s₂ » 0.

Рис. 1 – Нормальное падение плоской электромагнитной волны на границу раздела сред

Пусть из первой средына границу раздела сред при z = 0 падает линейно поляризованная плоская электромагнитная волна. Определим поле, в первой среде пользуясь общим уравнением для плоской электромагнитной волны:

, при z < 0, (1)

где: 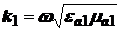– постоянная распространения, – волновое сопротивление первой среды.

Поле во второй среде естественно будем искать в том же виде:

, при z > 0 (2)

где: – постоянная распространения; – волновое сопротивление второй среды.

Первое слагаемое в уравнении (2), пропорциональное А^¢, дает волну, распространяющуюся от границы z = 0 вглубь среды с e_а2, m_а2, а второе слагаемое, пропорциональное В^¢, определяет волну, распространяющуюся в обратном направлении, т.е. к границе z = 0. Из физических соображений следует принять В^¢= 0 (поскольку очевидно, что волне во второй среде не от чего отражаться).

Тогда система уравнений (2) упроститься к виду:

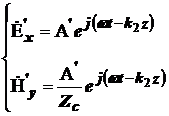, при z > 0. (3)

Воспользуемся теперь граничными условиями на границе сред при z = 0. При отсутствии поверхностного тока на границе раздела сред, касательные составляющие поля непрерывны, т.е. Е_t₁ = Е_t₂ и Н_t₁ = Н_t₂ , при z = 0.

Исходя из этого, получим: , ,

, ,

1 + Г = Т , 1 – Г = T ,

где: - называют коэффициентом отражения, - называют коэффициентом передачи.

Таким образом, имеем:

Решая данную систему уравнений относительно Г и T, получим:

, . (4)

С учетом введенных параметров Г и Туравнения для плоской электромагнитной волны в первой и второй среде можно соответственно записать следующим образом:

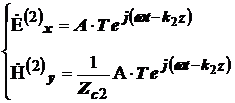Пользуясь этими уравнениями, изобразим, например Е_х, в первой и второй средах. Для изображения амплитуды электрического поля в первой среде воспользуемся векторной диаграммой, показанной на рис. 2.

Рис. 2 – Амплитуда напряженности электрического поля при нормальном падении волны на границу раздела сред

Из приведенного рисунка видно, что «волнистость» в первой среде определяется значением Г – коэффициентом отражения, другими словами, различием между Z_С1 и Z_С2, чем больше различие, тем больше «волнистость».

Рассмотрим два предельных случая:

1) Полное прохождение.

Если Z_С1= Z_С2, что возможно если 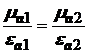, то из (4) следует, что Г = 0, Т = 1. То есть, отражение отсутствует, и амплитуда поля при переходе из одной среды в другую остается неизменной.

2) Полное отражение.

Пусть вторая среда является идеальным проводником (s₂ = ¥), тогда:

В этом случае из (4) следует, что: Г = – 1, Т = 0. То есть, поле во второй среде отсутствует (т.к. Т = 0), а в первой среде оно будет определяться выражениями:

. (5)

Как видно из (5) электрическая и магнитная составляющие сдвинуты относительно друг друга по фазе на 90⁰. Выражение для вектора Умова-Пойнтинга в этом случае примет вид:

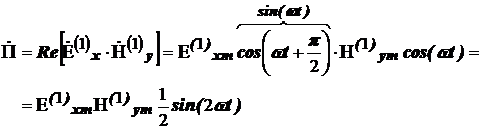
Напомним, что вектор Умова-Пойнтинга характеризует плотность потока мощности электромагнитного поля, переносимой через единичную площадку. Полученный результат означает, что мгновенное значение вектора Пойнтинга может принимать как положительные, так и отрицательные значения. Среднее же значение вектора Пойнтинга будет равно нулю. Следовательно, передачи энергии вдоль оси z не происходит, движение энергии имеет чисто колебательный характер. Электромагнитная волна такого вида называется стоячей волной. Свое название волна получила вследствие того, что минимумы (узла) и максимумы (пучности) составляющих поля не меняют своего положения на оси z.

Покажем это. Из системы уравнений (5) имеем:

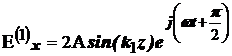
Перейдем от комплексных значений к мгновенным:

Проведем анализ амплитуды этой волны:

Е_m = 0 при z = 0, p/к₁, 2p/к₁ и т.д. Е_m = 2А при z = p/2к₁, 3p/2к₁ и т.д.

Поведение этой волны в различные фиксированные моменты времени показано на рис. 3. Несложно заметить, что положение узлов и пучностей не меняется с течением времени. Данное свойство стоячих волн широко используется на практике в измерительных целях (например, при измерении длины волны).

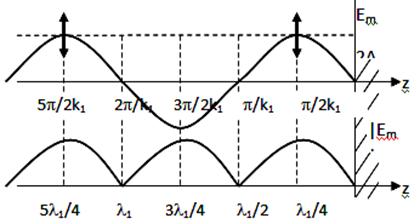
Рис. 3 – Стоячая волна

НАКЛОННОЕ ПАДЕНИЕ ПЛОСКОЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ НА ГРАНИЦУ РАЗДЕЛА СРЕД

В этом вопросе обсуждаются волновые явления на границе раздела сред при наклонном падении плоской волны, формулируются законы Снеллиуса и выводятся формулы Френеля.

Сделаем вначале несколько предварительных замечаний:

а) До сих пор мы рассматривали плоские волны, направление распространения которых совпадало с осью z. Рассмотрим распространение волны вдоль некоторой произвольной оси z`, не совпадающей с осью z (см. рис. 4).

Рис. 4 – Произвольное направление распространения плоской электромагнитной волны

Очевидно, что уравнение плоской электромагнитной волны в новой системе координат x` y` z` будет:

_х_` = Ае^-jkz'

_y` = Ae^-jkz’

Выразим величину z’ через исходные координаты х, y, z. Из математики известно, что, если определить ось z’ углами g₁, g₂, g₃ направляющих косинусов, как показано на рис. 4, то:

z’ = x×cosg₁ + y×cosg₂ + z×cosg₃ .

Тогда в исходной системе координат уравнение плоской электромагнитной волны примет вид:

. (6)

б) При наклонном падении линейно поляризованной волны на границу раздела сред возможны два случая:

1 случай: электрический вектор падающей волны параллелен плоскости раздела сред, т.е. падающая волна является волной с горизонтальной (параллельной) поляризацией.

2 случай: электрический вектор падающей волны перпендикулярен плоскости раздела сред, т.е. падающая волна является волной с вертикальной (нормальной) поляризацией.

Рассмотрим теперь оба эти случая более подробно.

1 случай. Плоская электромагнитная волна с горизонтальной поляризацией (рис. 5).

Рис. 5 – Наклонное падение плоской волны с горизонтальной поляризацией

Наиболее просто поле падающей волны выразить через систему координат x’, y’, z’:

Перейдем теперь к основной системе координат х, y, z. Для чего определим углы между осями Ох, Оy, Оz и осью Оz`:

g₁ = 90⁰ => cos(g₁) = 0, g₂ = 90⁰ – j₁ => cos(90 – j₁) = sinj_1,g₃ = j₁ => cosj₁

Следовательно, пользуясь выражением (6) получим:

. (7а)

Чтобы удовлетворить граничным условиям при z = 0 необходимо допустить существование отраженной и преломленной волны. Выражения для этих волн можно записать следующим образом:

Отраженная волна: Преломленная волна:

Переходим в систему координат х, y, z:

g₁ = 90⁰ => сos(g₁) = 0 g₁ = 90⁰ => cos(g₁) = 0

g₂ = 90 - j₂ => sinj₂ g₂ = 90 - j₃ => sinj₃

g₃ = 180 - j₂ => - cosj₂ g₃ = j₃ => cosj₃

Следовательно:

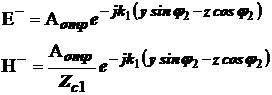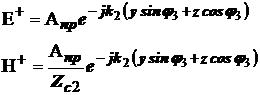(7б) (7в)

Теперь воспользуемся граничными условиями при z = 0, в соответствии с которыми, касательные составляющие вектора электрического и магнитного поля должны быть непрерывны:

Е_t₁ = Е_t₂; Н_t₁ = Н_t₂ при z =0.

Следовательно, с учетом рис. 5 и выражений (7) получим:

(8)

Поскольку граничное условие (8) должно выполняться на всей поверхности раздела сред (т.е. при любом значении координаты y), то это означает, что должны быть соблюдены равенства: k₁sinj₁ = k₁sinj₂ = k₂sinj₃

Из этих равенств вытекают так называемые законы Снеллиуса (голландского физика Снелла):

1) Угол падения j₁ равен углу отражения j₂.

2) Угол падения и угол преломления связаны зависимостью:

где: 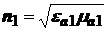, - называют коэффициентами преломления сред; n₁₂– называют относительным коэффициентом преломления. С учетом законов Снеллиуса граничные условия (8) принимают вид:

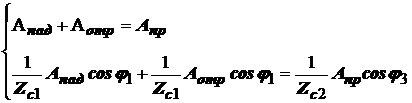Также, как в предыдущем разделе, введем понятие коэффициента отражения и передачи . Тогда:

Решая данную систему уравнений относительно и получим:

(9)

Полученные соотношения (9) называют формулами Френеля для волн с горизонтальной поляризацией.

2 случай. Плоская ЭМВ с вертикальной поляризацией (рис. 6).

Рис. 6 – Наклонное падение плоской волны с вертикальной поляризацией

Ход анализа аналогичен тому, как это проводилось для волны с горизонтальной поляризацией:

1) Записываем электрические и магнитные составляющие поля для падающей, отраженной и преломленной волны сначала в координатах х`, y`, z`, х``, y``, z`` и х```, y```, z```.

2) Переходим к основной системе координат х, y, z, учитывая соответствующие значения углов g₁, g₂, g₃.

3) Определяем граничные условия на поверхности раздела сред при z = 0:

Е_t₁ = Е_t₂; Н_t₁ = Н_t_2.

Пользуясь рис. 6, касательные составляющие легко определить как:

Чтобы данные граничные условия выполнялись при любом значении координаты y, необходимо выполнение равенств:

k₁sinj₁ = k₁sinj₂, k₁sinj₁ = k₂sinj₃,

т.е. чтобы соблюдались законы Снеллиуса, следовательно:

4) Вводим понятия коэффициента отражения Г^ = А_отр/А_п_ад и коэффициента передачи Т^ = А_пр/А_пад. Тогда:

Отсюда:

. (10)

Полученные соотношения носят название формул Френеля для волн с вертикальной поляризацией.

Дата добавления: 2018-05-12; просмотров: 1805; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!