ПОЛЯРИЗАЦИЯ ПЛОСКИХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

Стр 1 из 3Следующая ⇒

Лекция № 10.

Плоские электромагнитные волны

Учебные вопросы лекции:

Волновые уравнения Гельмгольца. Общее уравнение плоской электромагнитной волны.

Поляризация плоских электромагнитных волн.

Плоская электромагнитная волна в среде без потерь.

Плоская электромагнитная волна в реальной среде.

Введение

В данной лекции рассматриваются вопросы, связанные с наиболее простыми моделями электромагнитных волн, а именно: с плоскими электромагнитными волнами. Электромагнитное поле, возникающее в некоторой области пространства, не заполняет его мгновенно, а распространяется в виде волны с конечной скоростью, которая зависит от свойств среды. Это хорошо известное теперь свойство электромагнитного поля было предсказано Дж. К. Максвеллом задолго до того времени, когда экспериментально это было доказано Г. Герцем.

В целом, волна от источника в безграничном пространстве имеет сферический фронт и соответственно представляет собой сферическую волну (в качестве аналогии здесь можно предложить волны, расходящиеся от камня, брошенного в воду). Плоские волны, которые изучаются в данной лекции, являются идеализацией электромагнитного поля на большом расстоянии от источника. Тем не менее, во многих практических задачах реальные волны с успехом могут быть заменены плоскими электромагнитными волнами.

ВОЛНОВЫЕ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА. ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ

В первом вопросе лекции дается общая характеристика плоской электромагнитной волны, приводится математическое описание волновых процессов с помощью волновых уравнений Гельмгольца; рассматривается решение этих уравнений применительно к плоской электромагнитной волны.

Важнейшие свойства электромагнитных волн далее мы будем рассматривать на простейшем примере плоской однородной волны. Дадим ряд определений.

Волной в общем случае называют всякое изменяющееся во времени пространственное чередование максимумов и минимумом любой физической величины.

Для электромагнитной волны такой физической величиной являются напряженности электрического Е и магнитного Н полей.

Расположим в безграничном трехмерном пространстве декартовую систему координат (х, y, z) с начальной точкой О. Расположим в этой точке О некий источник электромагнитных волн. Пусть некоторая исследуемая область V лежит так далеко от источника, что любые две точки, лежащие в области V на плоскости перпендикулярной оси Оz, можно считать находящимися на одинаковых расстояниях от точки О (см. рис. 1).

Рис. 1 – К пояснению понятия плоская электромагнитная волна

В пределах этого допущения можно считать что отрезки ОМ₁ и ОМ₂ равны и параллельны.

Это означает, что точки М₁ и М₂ и следовательно, во всей области V процесс не зависит от координат х и y, т.е.:

Плоской электромагнитной волной называют такую электромагнитную волну, у которой во всех точках плоскости, перпендикулярной к направлению распространения, вектора поля и имеют одинаковые значения (т.е. = const, = const).

Фазовым фронтом волны называют поверхность, проходящую через точки с одинаковыми фазами. По форме этой поверхности определяют вид волны, например, сферическую или цилиндрическую волну. У плоской волны, как несложно увидеть из рис. 1, поверхность равных фаз представляет собой плоскость (z = const).

Волна называется однородной, если ее амплитуда постоянна во всех точках фазового фронта, и неоднородной, если ее амплитуда зависит от координат точек фазового фронта.

Изучение плоских волн имеет важное практическое значение, поскольку реально существующие поля излучения антенн могут быть с достаточной точностью заменимы этими волнами. (см. рис. 2).

Рис. 2 – Представление сферических волн в виде плоских

Действительно, если рассматривать излученные антенной волны в не-которой области V, размеры которой a, b и с весьма малы по сравнению с расстоянием R до антенны, то можно в пределах указанной области V заменить участки сферических (или более сложной формы) волновых поверхностей на параллельные плоскости, и рассматривать, таким образом, плоские электромагнитные волны.

Рассмотрим однородную среду с параметрами e_а, m_а, s, в которой отсутствуют сторонние источники ( _ст = 0, r_ст = 0) и свободные заряды (r = 0). Запишем первое уравнение Максвелла в комплексной форме для такой среды:

, (1)

где: - комплексная диэлектрическая проницаемость среды.

Изображая число 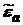на комплексной плоскости (см. рис. 3) можно характеризовать соотношение между вещественной и мнимой частями при помощи угла d, носящего название угла потерь, который определяется из соотношения:

. (2)

Рис. 3 – Изображение 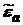на комплексной плоскости

Введение комплексной диэлектрической проницаемости и угла потерь позволяет весьма просто учитывать как диэлектрические, так и проводящие свойства конкретного вещества. Чем больше угол d, тем среда становится более проводящей, следовательно, увеличивается значение тока проводимости I_пр, протекающего в этой среде, следовательно, тем относительно большая часть электромагнитной энергии, распространяющаяся в этой среде, рассеивается в виде тепла.

Введем комплексную диэлектрическую проницаемость, полагая при этом, что магнитная проницаемость m_а – вещественная величина (это справедливо для подавляющего большинства диэлектрических сред). Запишем теперь 1-ое и 2-ое уравнения Максвелла:

Преобразуем 1-ое уравнение Максвелла следующим образом. Возьмем операцию rot от обеих частей уравнения:

Учитывая известное из высшей математики соотношени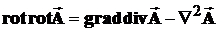е , где - произвольный вектор, левую часть уравнения преобразуем следующим образом:

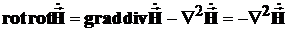Здесь учтено, что согласно 4-му уравнению Максвелла

Таким образом, окончательно получаем уравнение для комплексного вектора напряженности магнитного поля :

или . (3)

Введем обозначение , где параметр носит название постоянной распространения или волнового числа, в общем случае это комплексная величина.

Проделав подобные же преобразования со 2-м уравнением Максвелла, получим следующее уравнение для комплексного вектора напряженности электрического поля:

. (4)

Уравнения (3) и (4) носят название волновых уравнений Гельмгольца.

Из математической физики известно, что любые стационарные волновые процессы (будь то колебания пружины или колебания струны) описываются уравнениями Гельмгольца. Таким образом, из полученных уравнений (3) и (4) следует фундаментальный вывод из теории Максвелла:

Переменность во времени (поскольку мы рассматриваем уравнения Максвелла в комплексной форме) электрических и магнитных полей неизбежно приводит к распространению в пространстве электромагнитных волн.

На основании уравнений Гельмгольца несложно получить общее уравнение для плоской электромагнитной волны. Поскольку для плоской электромагнитной волны 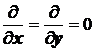, то из (4), раскрывая операцию Ñ² , получаем:

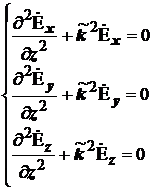(5)

Здесь и далее, для простоты записи, знак "®" вектор над составляющими поля, обозначающий векторную величину, опущен. Из 3-го уравнения Максвелла имеем: (поскольку мы условились, что в рассматриваемой среде свободных зарядов нет). Или раскрывая операцию div:

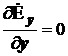, , . (6)

Подставляя полученные выражения в (5) получаем, что составляющая 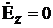, следовательно, получаем следующую систему дифференциальных уравнений:

, .

Общее решение этих односторонних дифференциальных уравнений в математике хорошо известно, и имеет вид:

, , (7)

где: произвольные комплексные амплитуды, включающие множитель e^j^w^t.

Составляющие электромагнитного поля проще всего определить, используя 2-ое уравнение Максвелла:

, отсюда .

Раскрывая операцию rot и учитывая, что , получим:

(8)

Упростим полученные выражения:

Аналогично

где: , носит название характеристического (волнового) сопротивления среды. В общем случае это комплексное число.

Уравнения составляющей электромагнитной волны (см. 7 и 8) распадаются на две независимых друг от друга системы уравнений:

, . (9)

Полученные выражения являются общим уравнением плоской электромагнитной волны. Проведем краткий анализ полученных уравнений:

1) Плоскую электромагнитную волну можно рассматривать как наложение двух не связанных друг с другом волн: волна, у которой вектор параллельный оси х, а вектор параллельный оси y, и волна, у которой вектор параллельный оси y, а вектор параллельный оси х.

2) Каждая из составляющих электромагнитного поля является суммой двух слагаемых: слагаемое, в которое входит множитель е ^-^jkz, представляет собой волну, распространяющуюся в сторону положительных значений осиz ; и слагаемое с множителем е ^jkz, которая представляет собой волну, распространяющуюся в обратную сторону (в сторону отрицательных значений оси z).

ПОЛЯРИЗАЦИЯ ПЛОСКИХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

В этом вопросе рассматривается явление поляризации электромагнитных волн, описываются различные виды поляризации и характер поведения волн.

В большинстве практических задач источники электромагнитных волн часто локализованы в одной области пространства (например, излучающая антенна). В этом случае в общем решении для плоской электромагнитной волны (9) должны быть оставлены лишь волны, бегущие от источников и распространяющиеся в направлении положительных значений координатыz:

, ,

где: произвольные комплексные амплитуды, включающие множитель e^j^w^t.

Для простоты будем полагать, что среда, в которой распространяется волна, является однородной (e_а, m_а – const), а ее удельная проводимость s » 0, тогда: .

Определим значения напряженности электрических и магнитных полей плоской электромагнитной волны:

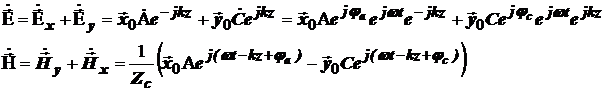
где: – единичные орты, j_а, j_с – произвольные начальные фазы соответствующих составляющих электромагнитной волны. Перейдем от комплексных значений к мгновенным:

(10)

Волну типа (10) можно рассматривать как суперпозицию двух плоских волн с взаимно перпендикулярной ориентацией векторов и , распространяющихся в одном направлении, т.е. вдоль оси z. Характер изменения вектора волны (10) с течением времени в фиксированной точке пространства зависит от соотношения между начальными фазами j_а и j_с и от амплитуд А и С. Плоскость, в которой происходит изменение вектора напряженности электрического поля в фиксированной точке пространства принято называть плоскостью поляризации.

Зафиксируем координату z (для определенности примем z = 0), тогда из (10) имеем:

где: - разность фаз между составляющими напряженности электрического поля.

Рассмотрим частные случаи:

1) или 180⁰, тогда:

(10, а)

где:

Из полученного выражения видно, что амплитуда Е_m изменяется от 0 до с течением времени с частотой w, а конец вектора перемещается вдоль отрезка прямой линии ОМ (см. рис. 4). Волны, обладающие таким свойством, принято называть линейно поляризованными.

Рис. 4 – Линейно поляризованная волна

В зависимости от положения плоскости поляризации среди линейно поляризованных волн различают:

- волны с нормальной (вертикальной) поляризацией, если А ¹ 0, С = 0;

- волны с параллельной (горизонтальной) поляризацией, если А=0, С ¹ 0.

2) , тогда:

(10, б)

где: , а выражение (cos wt + sin wt) представляет собой уравнение окружности.

Из полученного уравнения видно, что вектор остается неизменным по амплитуде и вращается с угловой частотой w, описывая окружность (см. рис. 5).

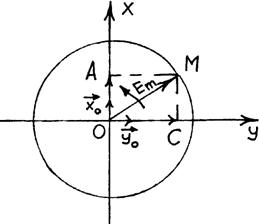
Рис. 5 – Волна с круговой поляризацией

Волны такого типа называют волнами с круговой поляризацией. В зависимости от направления вращения вектора различают:

- волны с левой круговой поляризацией (вращение против часовой стрелки), если ;

- волны с правой круговой поляризацией (вращение по часовой стрелке), если .

3) Все остальные углы Dj , помимо 0⁰, 90⁰, 180⁰ и 270⁰, тогда:

(10, в)

Полученное в скобках выражение является уравнением эллипса. Таким образом, конец вектора с течением времени перемещается вдоль эллипса с угловой частотой w (см. рис. 6).

Волны такого типа называют эллиптически поляризованными волнами. Если Dj лежит в пределах 0 ¸ 180⁰, то такая волна называется волной с левой эллиптической поляризацией. Если Dj лежит в пределах 180⁰ ¸ 360⁰, то такая волна называется волной с правой поляризацией.

Рис. 6 – Волна с эллиптической поляризацией

Общее замечание: Очевидно, что линейно поляризованная волна и волна с круговой поляризацией являются частными случаями эллиптически поляризованной волны.

Все то, что мы рассмотрели до сих пор в этом разделе, предполагалось при фиксированном значении координаты z. Введем координату z в вышеприведенные уравнения (10 а, б, в) для волн с различной поляризацией и изобразим поведение этих волн в фиксированные моменты времени t, см. рис. 7.

Рис.7 – Волна с вертикальной поляризацией (а) и с эллиптической поляризацией (б)

Несложно заметить, что проекция этих волн на плоскость xОy представляет собой:

- отрезок прямой;

- окружность;

Отсюда становится очевидным характер поляризации этих волн.

Дата добавления: 2018-05-12; просмотров: 2665; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!