Физические компоненты тензора.
Перейдем к физическим компонентам

| (101) |
Где все компоненты в цилиндрической системе координат будут такими же, кроме

| (102) |
Откуда для физических компонент получаем уравнения равновесия в инженерной трактовке

| (103) |
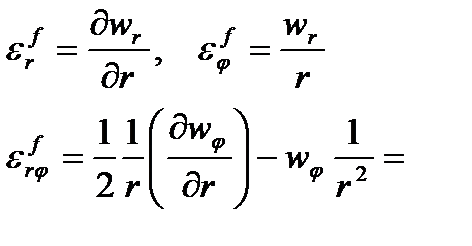
| (104) |
Одномерная задача о раздувании трубы.
Рассмотрим задачу раздувания трубы внутреннего радиуса а и внешнего радиуса в внутренним давлением ку.
Искомые функции зависят только от радиуса

| (105) |
Последнее уравнение интегрируется

| (106) |
Но из граничных условий получаем, что константа равна нулю.
Первое уравнение можно удовлетворить тождественно, введя функцию повреждения
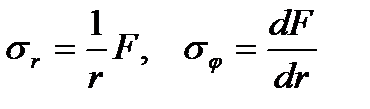
| (107) |
Из уравнений (94) получим в нашем случае

| (108) |
Откуда получаем уравнение совместности деформаций

| (109) |
Выразим в уравнении совместности деформаций компоненты тензора деформаций через компоненты тензора напряжений с помощью закона Гука

| (110) |
Из уравнений (109) и (110) получим

| (111) |
Откуда
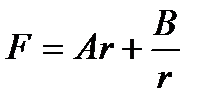
| (112) |
И з уравнений (107) получаем

| (113) |
Из граничных условий мы получаем систему уравнений для двух констант А и В.

| (114) |
Откуда

| (115) |
Из закона Гука можем получить

| (116) |
Одномерная задача о вращающемся диске
Рассмотрим задачу о вращающемся диске.
Искомые функции зависят только от радиуса

| (117) |
Это уравнение можно удовлетворить тождественно, введя функцию повреждения
|
|
|

| (118) |
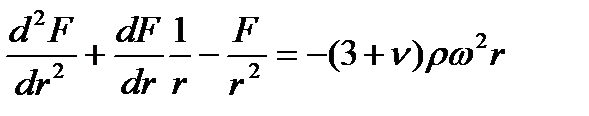
| (119) |
Откуда

| (120) |
И з уравнений (107) получаем

| (121) |
Постоянная В должна быть равна нулю, чтобы в центре диска были конечные напряжения. Вторая константа находится из условия свободной грани на внешнем радиусе.

| (122) |
Откуда
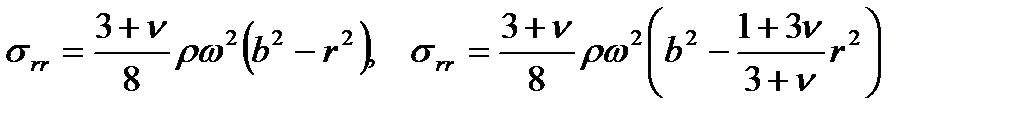
| (123) |
Лекция 8. Антиплоская задача теории упругости.
Кручение цилиндрических стержней.
Постановка задачи.
В рамках теории малых деформаций рассмотрим кручение цилиндрического стержня моментом, направленным вдоль третьей оси  , а плоскость поперечного сечения стержня будет лежать в координатной плоскости
, а плоскость поперечного сечения стержня будет лежать в координатной плоскости  , в декартовой системе координат.
, в декартовой системе координат.
Рассмотрим уравнение равновесия

| (124) |
Если мы добавим уравнения Бельтрами-Митчелла,

| (125) |
то система получится замкнутой, с учетом граничных условий.
Боковые поверхности и торцы свободны от усилий:

| (126) |
При этом задан крутящий момент

| (127) |
Полуобратныйметод Сен-Венана решения основывается на допущении вида поля перемещений, соответствующих кручению:
 Здесь введены две неизвестные – угол закручивания
Здесь введены две неизвестные – угол закручивания  и функция кручения и функция кручения  . .
| (128) |
Откуда мы получаем выражение компонент тензора деформаций

| (129) |
Из закона Гука находим напряжения
|
|
|

| (130) |
Первые два уравнения равновесия (124) выполняются тождественно, а третье дает уравнение Лапласа для функции кручения 
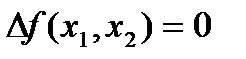
| (131) |
Граничные условия на боково й поверхности дают

| (132) |
Здесь мы использовали следующие равенства

| (133) |
То есть система уравнений (131) и (132) формулирует задачу Неймана.
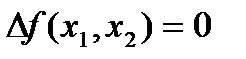 , , 
| (134) |
Граничные условия на торцах

| (135) |
Выполняются автоматически при подстановке (130), а условие равенства моменту:

| (136) |
Дает связь между углом крутки и приложенным моментом
Дата добавления: 2018-05-12; просмотров: 802; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
