Регрессионный анализ: понятие и сущность
Это метод математической статистики, позволяющий изучать зависимость среднего значения какой-либо величины от вариации другой величины или нескольких величин (в этом случае применяется множественный Р. а.). Понятие Р. а, ввел Ф. Гальтон, установивший факт определенного соотношения между ростом родителей и их взрослых детей. Он заметил, что у родителей самого низкого роста дети оказывались несколько выше, а у родителей самого высокого роста - ниже. Такого рода закономерность он назвал регрессией. Р. а. используется преимущественно в эмпирических психологических исследованиях при решении задач, связанных с оценкой какого-либо влияния (например, влияния интеллектуальной одаренности на успеваемость, мотивов- на поведение), при конструировании психологических тестов и т. д.
Дисперсионный анализ: сущность и задачи
Дисперсионный анализ – (от лат. dispersion – рассеивание) – статистический метод, позволяющий анализировать влияние различных факторов (признаков) на исследуемую (зависимую) переменную. Метод был разработан биологом Р. Фишером (1925) и применялся первоначально для оценки экспериментов в растениеводстве. В дальнейшем выяснилась общенаучная значимость дисперсионного анализа для экспериментов в психологии, педагогике и медицине и др.
Суть дисперсионного анализа состоит в разложении (дисперсии) измеряемого признака на независимые слагаемые, каждое из которых характеризует влияние того или иного фактора или их взаимодействия. Последующее сравнение таких слагаемых позволяет оценить значимость каждого изучаемого фактора, а также их комбинации.
|
|
|
Дисперсионный анализ используется преимущественно в экспериментальной психологии при изучении действия на испытуемых тех или иных факторов. При этом особую роль играет анализ средних значений (отклонения от которых и называют дисперсией).
В дисперсионном анализе возможны два принципиальных разделения всех исследуемых переменных на независимые переменные (факторы) и зависимые переменные (результативные признаки).
Первый путь состоит в том, что исследователь совершает какие-либо воздействия на испытуемых или учитываются какие-либо не зависящие от исследователя воздействия на них, и именно эти воздействия считаются независимыми переменными, или факторами, а исследуемые признаки рассматриваются как зависимые переменные, или результативные признаки. К примеру, возраст испытуемых или способ предъявления им информация считаются факторами, а обучаемость или эффективность выполнения задания - результативными признаки.
Второй путь предполагает, что исследователь, не совершая никаких воздействий, считает, что при разных уровнях развития одних психологических признаков, другие проявляются тоже по-разному. По тем или иным причинам исследователь решает, что одни признаки могут рассматриваться скорее как факторы, а другие – как результат действия этих факторов. К примеру, уровень интеллекта или мотивации достижения начинаем считать факторами, а профессиональную компетентность или социометрический статус - результативными признаками.
|
|
|
Второй путь весьма уязвим для критики. К примеру, предположили, что настойчивость – значимый фактор учебной успешности студентов. настойчивость принимается за воздействующую переменную (фактор), а учебную успешность – за результативный признак. Против этого сразу бывают выдвинуты сразу же два возражения. В первую очередь, успех может стимулировать настойчивость; во-вторых, как собственно, измерялась настойчивость? В случае если она измерялась с помощью метода экспертных оценок, а экспертами были соученики или преподаватели, которым известна учебная успешность испытуемых, то не исключено, что это оценка настойчивости будет зависеть от известных экспертам показателей успешности, а не на оборот.
|
|
|
Практическая часть контрольной работы.
Задание 1.
Даны случайные числа 8,7,6,8,8,4,5,9,7.
Определить среднее арифметическое, стандартное отклонение, асимметрию и эксцесс. Определить наличие нормального закона распределения.
Решение задания 1.
Вычислим среднее арифметическое. Для этого применим формулу:
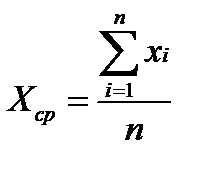 ,
,
где хi- i-е значение выборки;
i – порядковый номер значения в выборке;
n – объем выборки.
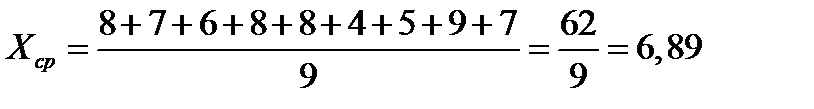
Вычислим стандартное отклонение по формуле:
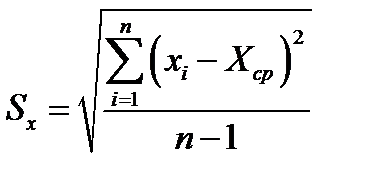
Предварительно нам необходимо рассчитать значение дисперсии:
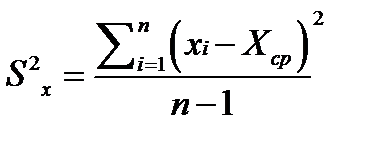
| № | хi | хi - 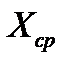
| (хi - 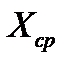 )2 )2
|
| 1 | 8 | 1,11 | 1,23 |
| 2 | 7 | 0,11 | 0,01 |
| 3 | 6 | -0,89 | 0,79 |
| 4 | 8 | 1,11 | 1,23 |
| 5 | 8 | 1,11 | 1,23 |
| 6 | 4 | -2,89 | 8,35 |
| 7 | 5 | -1,89 | 3,57 |
| 8 | 9 | 2,11 | 4,46 |
| 9 | 7 | 0,11 | 0,01 |
| n= 9 | 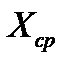 = 6,89 = 6,89
| Σ (хi - 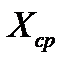 )2= 20,89 )2= 20,89
|
В соответствии с формулой рассчитаем значение дисперсии:
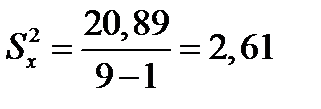
Произведем расчет стандартного отклонения.
Стандартное отклонение представляет собой квадратный корень из дисперсии.
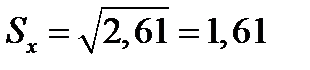
Нормальность распределения эмпирического показателя можно проверить путем расчета показателей асимметрии и эксцесса и сопоставления их с критическими значениями (Пустыльник Е.И., 1968, Плохинский Н.А., 1970 и др.).
|
|
|
Асимметрия– мера, показывающая степень и направление асимметричности графика. Обозначается Аs и находится по формуле:
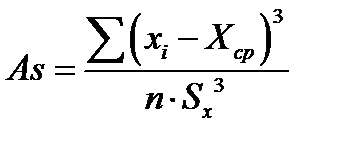
Эксцесс– греческое слово, обозначающее свойство остроконечности кривой. Обозначается Еx и находится по формуле:
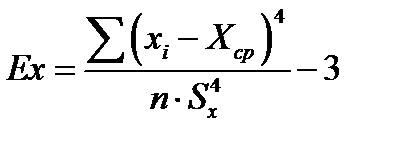
Ошибки репрезентативности асимметрии и эксцесса находятся по формулам:
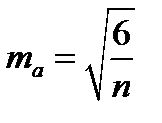 ;
; 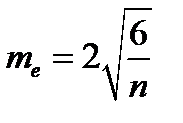
Величина допустимых отклонений асимметрии и эксцесса определяется стандартными ошибками асимметрии и эксцесса. Для асимметрии и эксцесса стандартные ошибки рассчитываются по следующим формулам:
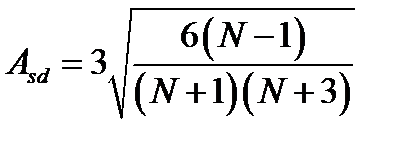
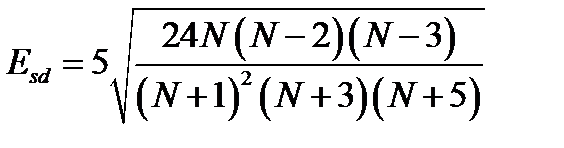
Выборочные значения асимметрии и эксцесса не отличаются от нуля, если они не превышают значения своих стандартных ошибок. Это можно считать признаком соответствия выборочного распределения нормальному закону.
Порядок расчетов:
а) определим показатели асимметрии и эксцесса по формулам Н.А. Плохинского и сопоставим их с критическими значениями, указанными Н.А. Плохинским;
б) рассчитаем критические значения показателей асимметрии и эксцесса по формулам Е.И. Пустыльника и сопоставим с ними эмпирические значения;
в) если эмпирические значения показателей окажутся ниже критических, сделаем вывод о том, что распределение признака не отличается от нормального.
Вычисление показателей асимметрии и эксцесса
| № | 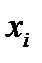
| 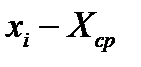
| 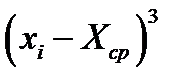 
| 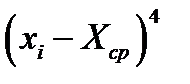
|
| 1 | 8 | 1,11 | 1,37 | 1,52 |
| 2 | 7 | 0,11 | 0,00 | 0,00 |
| 3 | 6 | -0,89 | -0,70 | 0,63 |
| 4 | 8 | 1,11 | 1,37 | 1,52 |
| 5 | 8 | 1,11 | 1,37 | 1,52 |
| 6 | 4 | -2,89 | -24,14 | 69,76 |
| 7 | 5 | -1,89 | -6,75 | 12,76 |
| 8 | 9 | 2,11 | 9,39 | 19,82 |
| 9 | 7 | 0,11 | 0,00 | 0,00 |
| n= 9 | 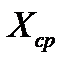 = 6,89 = 6,89
| 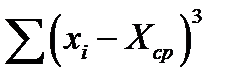 = -18,09 = -18,09
| 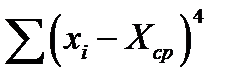 = 107,53 = 107,53
|
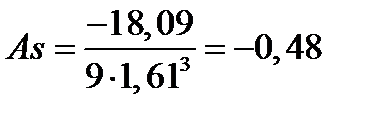 ;
; 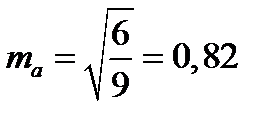
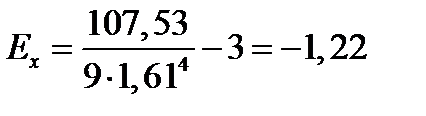 ;
; 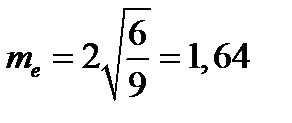
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают по абсолютной величине свою ошибку репрезентативности в 3 и более раз:
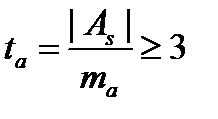 ;
; 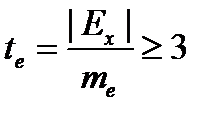
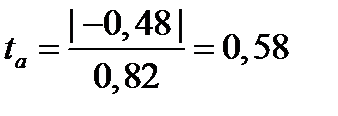 ;
; 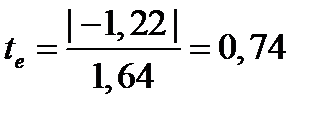
Мы видим, что оба показателя не превышают в три раза свою ошибку репрезентативности, из чего мы можем заключить, что распределение данного признака не отличается от нормального.
Теперь произведем проверку по формулам Е.И. Пустыльника. Рассчитаем критические значения для показателей Аs и Еx:
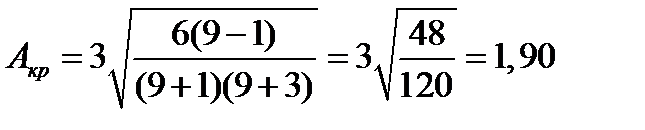 ;
;
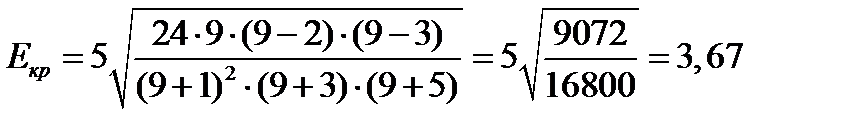
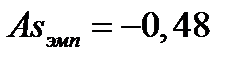 Asэмп < Asкр
Asэмп < Asкр
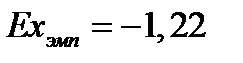 Exэмп < Еxкр
Exэмп < Еxкр
Таким образом, оба варианта проверки, по Н.А. Плохинскому и по Е.И. Пустыльнику, дают один и тот же результат: распределение результативного признака в данной задаче не отличается от нормального распределения.
Задание 2.
Дано Xср = 3,4, Sx = 0,7, n=45 и Yср = 4,8, Sy = 0,5, n = 50
Определить с помощью t-критерия Стьюдента и F-критерия Фишера различия между средними значениями и стандартными отклонениями.
Решение задания 2.
Проверим равенство генеральных средних обеих совокупностей.
Н0: Xср = Yср ; Н1 : Xср 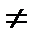 Yср.
Yср.
Представим данные в виде таблицы:
| X | Y | |
| n | 45 | 50 |
| ср | 3,4 | 4,8 |
| S | 0,7 | 0,5 |
Вычислим эмпирическое значение t-критерия Стьюдента по формуле:
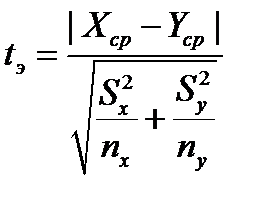
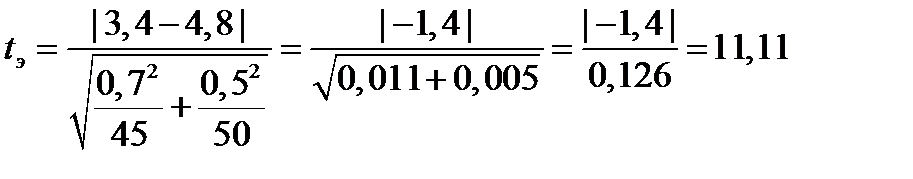
Вычислим число степеней свободы по формуле:
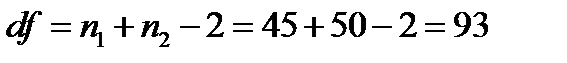
Определим по таблице критических значений критерия t-Стьюдента уровень значимости. Для df = 93. В таблице критическое значение есть только для df = 90 и df = 100. Большее число степеней свободы брать нельзя, поэтому берем критическое значение для df = 90. На уровне значимости α = 0,01 отвергаем нулевую гипотезу и принимаем альтернативную. Можно заключить, что средние значения в группах достоверно различаются.
С помощью критерия Фишера проверим гипотезу о равенстве стандартных отклонений распределений, из которых извлечены выборки.
Н0: 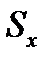 =
= 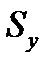 ; Н1:
; Н1: 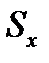
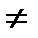
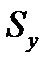
Найдем критическое число 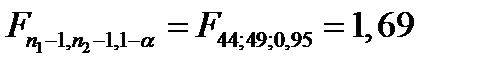 (по таблице критических значений Фишера) и сравним его со значением статистики критерия.
(по таблице критических значений Фишера) и сравним его со значением статистики критерия.
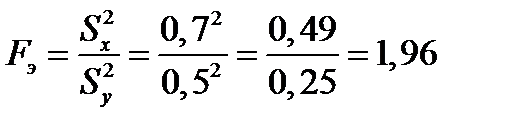 >1,69
>1,69
На уровне значимости α = 0,05 отвергаем нулевую гипотезу и принимаем альтернативную. Стандартные отклонения распределения из которых извлечены выборки, не равны.
Дата добавления: 2018-05-12; просмотров: 260; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
