Дать определение подсхемы СФЭ и указать правила применения к ней тождеств.
С хема Σ_ называется подсхемой схемы Σ, если V(Σ’)⊆ V (Σ), E(Σ’)⊆ E (Σ) и любая вершина v, v ∈ V (Σ’), которая либо относится к множеству входов (выходов) Σ, либо служит конечной (соответственно, начальной) вершиной некоторого ребра из E(Σ)\E(Σ’), является входом (соответственно, выходом) Σ’.
Тождества: отождествление переменных, соединение/разделение полюсов
3. Привести основные тождества, связанные с:
a) дистрибутивностью конъюнкции относительно дизъюнкций – в классах формул и СФЭ;
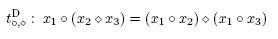
b) снятием “висячего” ФЭ отрицания – в классе СФЭ;
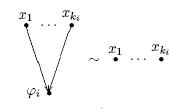
c) перебрасыванием контакта в трюхполюсной схеме - в классе КС.
Дать определение суммарного цикломатического числа КС и сформулировать утверждение о его изменениях при применении основных тождеств.
|E (G)| − |V (G)| + |c (G)| называется цикломатическим числом графа G. множество вершин V = V (G) и множество ребер E = E (G) множество всех связных компонент обозначается через c (G)
Для КС Σ от БП x1, . . . , xn и набора α, α ∈ Bn, определим величину Θ(Σ, α) = |E (Σ|α)| − |V (Σ|α)| + |c (Σ|α)| ,которая задает цикломатическое число графа Σ|α. Положим, далее,Θ(Σ) = α∈Bn Θ(Σ, α) .
Если Σ_ (x1, . . . , xn) ⇒{t1−t5}Σ’’(x1, . . . , xn), то Θ(Σ’) = Θ(Σ’’), а если Σ’⇒τkΣ’’, где k < n, то Θ(Σ’)−Θ(Σ’’) делится на 2n−k.
Тест № 5
1. Определение глубины D(f) ФАЛ f(x1…xn) и её тривиальная нижняя оценка для существенной ФАЛ f.
|
|
|
D (f)=minD(Σ) - глубина ФАЛ f относительно функционала L
Σ реал f,
2. Определение функции Шеннона LC(n) и её верхняя оценка, получаемая методом Шеннона.
L(n) = max L(f), f принадлежит P2(n)-Функция Шеннона для класса UC относительно функционала сложности L.
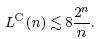
3. Нижняя мощностная оценка функции Шеннона LФ(n) и то соотношение, из которого она выводится.
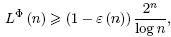
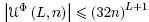γ = 0, a= 32n, y = LΦ(n) + 1, если U = UΦ;
4. Верхняя оценка функции Шеннона Lk(n), получаемая асимптотически наилучшим способом.
Утверждение о нижней оценке сложности КС, реализующей заданную систему ФАЛ, и асимптотика сложности контактного дешифратора.
Для любой ФАЛ f, f ∈ P2 (n), существует реализующая ее КС Σf такая, что
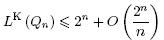
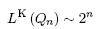
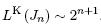
1. Определение сложности LC(f) ФАЛ f в классе СФЭ и её тривиальная нижняя оценка для существенной ФАЛ f.
LC (f)=minL(Σ) - сложность ФАЛ f в классе U C относ функционала L
Σ реал f,
U C Э Σ
LC (f)>=n-1
2. Определение функции Шеннона LФ(n) и её верхняя нижняя оценка, получаемая с помощью моделирования совершенной ДНФ на основе контактного дерева.
L(n) = max L(f), f принадлежит P2(n)-Функция Шеннона для класса UФ относительно функционала сложности L.
3. Нижняя мощностная оценка функции Шеннона Lk(n) и то соотношение, из которого она выводится.
|
|
|
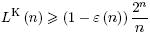
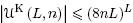γ = 1, a= 8n, y = LK(n), если U = UK;
Верхняя оценка функции Шеннона D(n), получаемая асимптотически наилучшим способом
Определение регулярного множества наборов единичного куба и формулировка утверждения о разбиении куба на такие подмножества.
Множество δ, δ ⊆ Bq, называется m-регулярным множеством наборов куба Bq, если m < q, |δ| = 2m, и все префиксы длины m наборов из δ различны. Для любого m-регулярного множества наборов δ, δ ⊆ Bq, система множеств ∆ = (δ1, . . . , δ2q−m), где δi = δ⊕α и ν (α) = i−1 при всех i, i = 1, . . . , 2q−m, образует разбиение куба Bq на m-регулярные подмножества.
1. Определение сложности Lk(f) ФАЛ f(x1…xn) в классе КС и её тривиальная нижняя оценка для существенной ФАЛ f.
Lk (f)>=n
2. Определение функции Шеннона D(n) и её верхняя оценка, получаемая с помощью моделирования совершенной ДНФ.
D(n) = max D(f), f принадлежит P2(n)-Функция Шеннона для класса U относительно функционала глубины D.
3. Нижняя мощностная оценка функции Шеннона LC(n) и то соотношение, из которого она выводится.
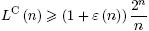
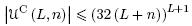γ = 1, a= 32, y= LC(n) + n, если U = UC;
4. Верхняя оценка функции Шеннона LФ(n), получаемая асимптотически наилучшим способом.
|
|
|
LФ(n)<2n/logn
Дата добавления: 2018-05-12; просмотров: 309; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!