Сформулировать утверждение о переходе от КПСТ для ЭП формул к КПСТ для ЭП СФЭ.
Пусть τ — КПСТ для ЭП формул из UΦБ, а Π’ и Π — системы тождеств для перехода от базиса Б к базису Б’ и от базиса Б’ к базису Б соответственно. Тогда система тождеств {Π’ (τ ) ,Π’ (Π)} является КПСТ для ЭП формул из UΦБ
Дать определение тождества для СФЭ, и его подстановки.
эквивалентностьсхем Σ’и Σ’’из U имеет место тогда и только тогда, когда Σ’и Σ’’реализуют равные системы (матрицы) ФАЛ предполагается, что соответствующие друг другу полюса (выходы, входы) в Σ’и Σ’’ имеют одинаковые пометки, а эквивалентность Σ’ и Σ’’записывается в виде тождества t : Σ’ ∼ Σ’’. Для схем из U, как и для формул, определяется ряд «простейших» преобразований, сохраняющих эквивалентность схем, которые называются подстановками. Тождество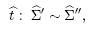 
которое получается в результате применения одной и той же подстановки к обеим частям тождества t : Σ’ ∼ Σ’’, называется подстановкой тождества t.
Дать определение подформулы данной формулы и указать правила применения к ней тождеств.
формулы, полученные в процессе индуктивного построения формулы F, называются ее подформулами. для формул имеет место так называемый принцип эквивалентной замены. Это означает, что если подформулу F’(подформулу F’’)формулы F заменить, учитывая тождество t эквивалентной ей формулой F’’(соответственно F’), то полученная в результате такой замены формула ˇF будет эквивалентна формуле F, то есть будет справедливо тождество ˇt : F = ˇF .
|
|
|
Аналогичный переход от F к F’ в результате применения одного из тождеств системы τ (нескольких последовательных применений тождеств из τ ) будем записывать в виде однократной (соответственно кратной) выводимости вида F →τ F’ (соответственно F ⇒|τ F’). При этом считается, что тождество t : F = F’ выводится из системы тождеств τ
3. Привести основные тождества, связанные с:
a) подстановкой константы 0 в конъюнкцию – в классах формул и СФЭ;
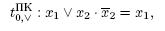
b) снятием “висячего” входа – в классе СФЭ;
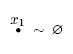
c) формульным тождеством вида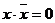 
– в классе КС.
Дать определение разделяющей КС и сформулировать лемму Шеннона.
Схема называется разделительной по входам(выходам), если ФАЛ проводимости между любыми ее различными входами (соответственно выходами) равна 0. Пусть КС Σ является результатом стыковки вида Σ = Σ’’(Σ’), а F, F’ и F’’ — матрицы, реализуемые КС Σ, Σ’ и Σ’’ соответственно. Тогда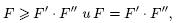 
если КС Σ’’ разделительна по входам или КС Σ’разделительна по выходам.
Дать определение тождества для КС, и его подстановки.
эквивалентность КС Σ’ = Σ’(x1, . . . , xn; a1, . . . , am) и Σ’’= Σ’’(x1, . . . , xn; a1, . . . , am) означает, что для любых i и j из отрезка [1,m] ФАЛ проводимости от ai к aj в КС Σ’равна ФАЛ проводимости от ai к aj в КС Σ’’. Определим подстановку для КС как переименование (с возможным отождествлением и инвертированием) БП, а также переименование (с возможным отождествлением и снятием) полюсов.
|
|
|
Дата добавления: 2018-05-12; просмотров: 240; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!