Определение пучка, регулярной точки и регулярной грани.
Тест №1
Определение элементарной конъюнкции и ДНФ.
Функции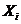 
и 
будем называть буквами БП 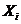и, как обычно, будем считать, что 
= , 
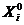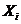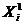= . Конъюнкция (дизъюнкция) r, 1 < r < n букв различных БП из множества X (n) называется элементарной конъюнкцией (соответственно элементарной дизъюнкцией) ранга r от булевых переменных X (n).
Дизъюнкция различных элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ)
Определение нерасширяемой ДНФ.
Любая ДНФ A’, которую можно получить из ДНФ A путем формирования в ней с помощью тождеств ассоциативности и коммутативности подформул вида xiK’ ∨ не(xi)K’’, применения к этим подформулам тождества обобщенного склеивания xiK’ ∨ xiK’’ = xiK’ ∨ не(xi)K’’ ∨ K’K’’ и последующего приведения подобных, называется расширением ДНФ A.
Определение ДНФ сумма тупиковых.
ДНФ пересечение тупиковых (сумма тупиковых) ФАЛ f, есть дизъюнкция всех тех различных простых импликант этой ФАЛ, которые входят в любую (соответственно хотя бы в одну) тупиковую ДНФ ФАЛ f.
Критерий вхождения простых импликант в ДНФ пересечение тупиковых.
Дизъюнктивная нормальная форма ∩T ФАЛ f состоит из тех простых импликант ФАЛ f, которые соответствуют ядровым граням этой ФАЛ.
Определение импликанты и простой импликанты.
Будем говорить, что ФАЛ f’ имплицирует ФАЛ f’’, если Nf’ ⊆ Nf’’ , то есть импликация (f’ → f’’) тождественно равна 1. Элементарная конъюнкция, которая имплицирует ФАЛ f, называется импликантой этой ФАЛ. Импликанта K ФАЛ f называется простой импликантой этой ФАЛ, если она не поглощается никакой другой отличной от нее импликантой ФАЛ f.
|
|
|
Определение минимальной ДНФ и кратчайшей ДНФ.
минимальная (кратчайшая) ДНФ ФАЛ f, есть ДНФ, которая имеет минимальный ранг (соответ-
ственно длину) среди всех ДНФ, реализующих f.
Определение ядровой точки, ядровой грани и ДНФ Квайна.
Набор α, α ∈ Bn, называется ядровой точкой ФАЛ f (x1, . . . , xn), если α ∈ Nf и α входит только в одну максимальную грань ФАЛ f. При этом грань NK, являющаяся максимальной гранью ФАЛ f и содержащая точку α, считается ядровой гранью ФАЛ f
Дизъюнктивная нормальная форма, получающаяся из сокращенной ДНФ ФАЛ f удалением тех ЭК K, для которых грань NK покрывается ядром ФАЛ f, но не входит в него, называется ДНФ Квайна этой ФАЛ.
Формулировка утверждения, связанного с построением сокращенной ДНФ из какой-либо КНФ.
Если неприводимая ДНФ A получается из КНФ B ФАЛ f в результате раскрытия скобок и приведения подобных, то A — сокращенная ДНФ ФАЛ f.
Определение сокращённой ДНФ.
|
|
|
Дизъюнкция всех простых импликант ФАЛ f называется ее сокращенной ДНФ.
Определение тупиковой ДНФ.
Будем говорить, что ДНФ A, реализующая ФАЛ f, является тупиковой ДНФ, если f не= A’для
любой ДНФ A’, полученной из A в результате удаления некоторых букв или целых ЭК.
Определение пучка, регулярной точки и регулярной грани.
Для ФАЛ f (x1, . . . , xn) и набора α, α ∈ Nf , обозначим через Πα (f) множество всех проходящих через α максимальных граней ФАЛ f, которое мы будем называть пучком
ФАЛ f через точку α. Точку α, α ∈ Nf , будем называть регулярной точкой ФАЛ f, если найдется точка β, β ∈ Nf ,для которой имеет место строгое включение Πβ (f) ⊂ Πα (f).
Грань NK ФАЛ f называется регулярной гранью этойФАЛ, если все точки NK регулярны.
Дата добавления: 2018-05-12; просмотров: 582; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!