В частном случае, когда температура на поверхности тела постоянна

t₀ = const

Граничные условия второго рода.Задается распределение теплового потока по поверхности тела для любого момента времени

q₀ =(x, y, z, τ)

в частном случае плотность теплового потока на поверхности не меняется

q_п = q ₀ = const

Граничные условия третьего рода. Задается температура окружающей среды и закон теплообмена между поверхностью тела и окружающей средой.

Граничные условия четвертого рода. Известны условия теплообмена тел с окружающей средой по закону теплопроводности Они применяются для решения задач методами моделирования или тепловых аналогий.

Стационарная теплопроводность

Согласно закону Фурье тепловой поток, передаваемый теплопроводностью, пропорционален коэффициенту теплопроводности, градиенту температуры и площади поверхности тела    

                                            2.4

где λ – теплопроводность вещества, Вт/ (м. К), характеризует способность данного вещества проводить теплоту. Значения величин теплопроводности различных веществ приводятся в справочниках теплофизических свойств.

В уравнении (2.4) тепловой поток и градиент температур - векторные величины и направлены в противоположные стороны, что отражает знак минус. В газах носителями тепловой энергии являются хаотически движущиеся молекулы. В металлах теплопроводность происходит в основном за счет теплового движения электронов. Теплопроводность веществ зависит от температуры, давления, примесей, пористости.

 Наиболее простыми случаями решения задач теплопроводности являются стационарные одномерные процессы тел простой формы.

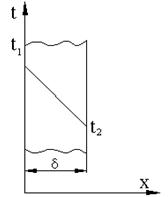Однослойная плоская стенка. Для определения теплового потока, проходящего через плоскую однослойную стенку толщиной δ, на двух поверхностях которой поддерживаются температуры t₁ и t_2, температура изменяется по толщине стенки. Применим закон Фурье:

 

Q = q F = ( t₂ – t₁)λ F / δ                        2.5

  Отношение λF /δ ( Вт/ К) называется тепловой проводимостью стенки, а обратная величина δ/(λ F) =R ( К/Вт ) - тепловым или терми ческим сопротивлением стенки. Изменение температур при λ = соnst происходит по прямой наклонной линии, наклон зависит от толщины и теплофизических свойств стенки. 

 

Рис.2.2 Распределение температуры по толщине плоской стенки

Многослойная плоская стенка. Формулой 2.5 удобно пользоваться для расчетов процессов теплопроводности в плоских стенках, состоящих из нескольких слоев, плотно прилегающих друг к другу.                 

                              2.6.

Плотность теплового потока, проходящего через все слои, одинакова, а теплопроводность слоев различна, температура падает более резко в слоях с меньшей теплопроводностью.                                             

Рис 2.3. Изменение температуры в многослойной плоской стенке

 

Определив тепловой поток, проходящий через многослойную плоскую стенку, можно определить падение температуры в каждом слое.                                                                                                                                                                                                   

Для рассматриваемого примера                       

t_{2 =} t₁ – q δ₁/ λ₁                                  2.7

t_{3 =} t₄ + q δ₃ /λ₃                     2.8

Температура в каждом слое стенки при постоянной теплопроводности изменяется по линейному закону и для многослойной стенки температурный график имеет вид ломаных линий.                  

Иногда многослойную плоскую стенку рассматривают как однослойную, вводя эквивалентную теплопроводность λ_экв.  Эквивалентная теплопроводность многослойной стенки равна теплопроводности однородной стенки той же толщины, с теми же температурами кратных поверхностей и пропускающими тот же тепловой поток.

                                                                           2.9.

Эквивалентная теплопроводность зависит от толщины слоев и термических сопротивлений. Тепловой поток можно определить:

                                    2.10.

Цилиндрическая однослойная стенка. Рассмотрим трубу бесконечной длины с постоянными температурами t₁ и t₂ на внешней и внутренней поверхностях соответственно.

Рис.2.3 Распределение температуры по толщине однослойной цилиндрической стенки

Изотермические поверхности будут цилиндрическими, имеющими с трубой общую ось. Температура и тепловой поток изменяют ся в направлении радиуса – t = ƒ (r), где r - текущая цилиндрическая координата.

Основываясь на законе Фурье, тепловой поток для трубы длинной l можно рассчитать по формуле

Q = 2πλ ℓ ( t ₁ - t ₂) /ln (d₂/d₁).                                    2.11.      

В цилиндрической трубе тепловой поток может быть отнесен либо к 1 м² внутренней или внешней поверхности, либо к единице длины l трубы:

Q/F_вн = q_вн, Q / F_внеш = q_внеш, соответственно q_вн > q_внеш, Q / ℓ = q_l, тогда

q_l = Q / ℓ= 2πλ(t₂ - t₁ )/ ln (d₂/d₁) ;                           2.12

q_вн = Q / (πd₁ℓ) = 2λ( t₂ – t₁) / ( d₁ln (d₂ / d₁));                   2.13

q_внеш = Q/ ( πđ₂ℓ) = 2λ ( t₂ – t₁) / (d₂ln (d₂ /d₁)).                  2.14

Многослойная цилиндрическая стенка. При известных и постоянных температурах на внутренней и наружной поверхностях температура изменяется вдоль радиуса. Тепловой поток определяется:

                                           2.15.

По формуле 2.15 рекомендуется считать при больших отношениях наружного и внутреннего диаметров d _н / d _вн ≥1,5. При меньших соотношениях диаметров целесообразно считать по аналогичным формулам для плоской стенки.

Шаровая стенка. При постоянных температурах t_ст1 и t_ст2 на внутренней (радиусом r₁) и наружной (радиусом r₂) поверхностях тепловой поток можно определить

Q = 4πλ (t _ст1 – t _ст2)/ (1/ r ₁ – 1/ r ₂)                2.16

---

Дата добавления: 2018-05-12; просмотров: 314; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!