Коридорное Шахматное
Характер движения жидкости, омывание труб каждого ряда и теплообмен в пучке зависит от расположения труб. Основными характеристиками пучков труб являются: внешний диаметр труб – dвнеш; количество рядов труб по движению жидкости – n, расстояние между осями диаметров по ширине –s1 и глубине пучка – s2; отношение расстояния между осями труб по ширине пучка к внешнему диаметру трубы – s1/dвнеш; отношение расстояния между осями двух соседних рядов труб по направлению движения жидкости к внешнему диаметру труб – s2/d внеш.
Омывание трубок первого ряда независимо от расположения труб в пучке практически не отличается от омывания одиночной трубы поперечным потоком жидкости и зависит от начальной турбулентности потока. Характер омывания следующих рядов труб в обоих пучках изменяется.
При коридорном расположении трубы любого ряда затеняются соответствующими трубами предыдущего ряда, что ухудшает омывание лобовой части, и большая часть поверхности трубы находится в слабой вихревой зоне. При шахматном расположении труб загораживания одних труб другими не происходит. Вследствие этого коэффициент теплоотдачи при шахматном расположении труб в одинаковых условиях выше, чем при коридорном.
При любом расположении труб каждый ряд вызывает дополнительную турбулизацию потока. Поэтому коэффициент теплоотдачи для труб второго ряда выше, чем для первого, а для третьего ряда выше, чем для второго. Начиная с третьего ряда поток жидкости стабилизируется и коэффициент теплоотдачи для всех последующих рядов остается постоянным.
|
|
|
Если теплоотдачу третьего ряда принять за 100%, то теплоотдача первого рада коридорных и шахматных пучков составляет 60%. Теплоотдача второго ряда коридорного пучка составляет 90%, а шахматного- 70%.
Теплоотдача в шахматных пучках выше, чем в коридорных за счет большей турбулизации потока.
Теплоотдача в пучках зависит от расстояния между трубами. Эта зависимость учитывается поправочным коэффициентом ε0, представляющим влияние относительных шагов.
Для глубинных рядов коридорного расположения пучка ε0 = ( s2/d)- 0,15 ; для шахматного при s1/s2<2 εs = ( s1/s2 )0,166, при ( s1 / s2 )>2 εs = 1,12.
При расчете теплообменных аппаратов и определении среднего коэффициента теплоотдачи третьего ряда пучка труб при смешанном режиме Re = 1.103 – 105 применяются следующие зависимости:
при коридорном расположении труб
Nuж = 0,26Reж0,65Рrж0,33 ( Рrж / Рrст )0,25 εs 2.52
При коридорном расположении труб
Nuж = 0,41Reж0,6 Рrж0,33 ( Рrж / Рrст)0,25 εs 2.53
Для воздуха при коридорном расположении пучка труб
|
|
|
Nuж = 0,194 Reж0,65 2.54
При шахматном расположении
Nuж = 0,35 Reж0,6 2.55
При вычислении чисел подобия за определяющую температуру принята средняя температура жидкости, за определяющую скорость – скорость жидкости в самом узком сечении ряда; за определяющий размер – диаметр трубы. Формулы справедливы для любых капельных жидкостей и газов.
Значение коэффициента теплоотдачи для труб первого ряда определяется путем умножения коэффициента теплоотдачи для третьего ряда на поправочный коэффициент εs = 0,6; для труб второго ряда в шахматных пучках – на εs = 0,7, а в коридорных – на εs = 0,9.
Среднее значение коэффициента теплоотдачи для всего пучка труб в целом определяется по формуле осреднения
α = ( α1F1 + α2F2 + ….. + αnFn)( F1 + F2 + …. + Fn ) 2.56
где: α 1, α 2,…. αп – средние коэффициенты теплоотдачи в отдельных рядах труб; F1, F2 F3- поверхности нагрева каждого ряда.
Если пучок труб омывается вынужденным потоком жидкости под углом менее 900, то коэффициент теплоотдачи, полученный при угле атаки 900, следует умножить на поправочный коэффициент εΨ
|
|
|
| φ, град | 90 | 80 | 70 | 60 | 50 | 40 | 30 | 20 | 10 |
| εφ | 1 | 1 | 0,98 | 0,94 | 0,88 | 0,78 | 0,67 | 0,52 | 0,42 |
Теплообмен при вынужденном движении жидкости вдоль пластины при ламинарном режиме при Re < 1.10 4 можно рассчитывать по формулам
Nuж = 0,66 Reж0,5Рrж0,33 (Рrж/ Рrст)0,25 2.57
Для воздуха формула упрощается
Nuж = 0,57Reж0,5 2.58
Теплообмен при вынужденном движении жидкости вдоль пластины при турбулентном режиме при Re > 4.104 можно определить
Nuж = 0,037Reж0,8Рrж0,43(Рrж / Рrст)о,25 2.59
Для воздуха при Рr ≈ 0,7 = соnst уравнение упрощается
Nuж = 0,032 Reж0,8 2.60
За определяющую температуру принята температура жидкости вдали от пластины, за определяющий размер принята длина пластины по направлению потока.
Теплообмен жидких металлов. Иногда в качестве рабочих жидкостей применяют расплавленные металлы, обладающие значительными достоинствами по сравнению с газами и жидкостями. Высокую температуру можно получить с водяным паром, но требуется большое давление. Газы имеют малый коэффициент теплоотдачи и небольшую теплоемкость. Жидкие металлы имеют высокую температуру кипения, большие коэффициенты теплоотдачи и термически устойчивы.
|
|
|
В качестве теплоносителей применяют натрий, калий, натриево-калиевые сплавы, литий, олово и др.
При Re ≈ 104- 106, Рr = 0,004 – 0,032 и ℓ/ d > 30 для определения коэффициентов теплоотдачи при вынужденном турбулентном течении щелочных и тяжелых металлов применяется формула
Nuж = 4,8 + 0,014 (ReжРrж )0,8 2.61
Приведенная формула справедлива для чистых поверхностей нагрева и герметичных контуров нагрева, заполненных нейтральными газами.При свободном движении щелочных и тяжелых металлов и их сплавов применима формула
Nuж = С.GrnPr0,24 2.62
При ламинарном режиме Gr = 102 – 109 C = 0,52 и n = 0,25
При турбулентном режиме Gr = 109 – 1013 C = 0,106 и n = 0,33
За определяющую температуру принята средняя температура пограничного слоя t = 0,5 (tж + tст ); за определяющий размер принята для горизонтальных труб – внешний диаметр, для вертикальных пластин – их высота.
Теплообмен при свободном течении жидкости Аналитические решения задачконвективного теплообмена при свободном ламинарном и турбулентном движении выполнены при целом ряде упрощающих предпосылок, поэтому эти решения большого практического применения не получили. Решение задач по определению коэффициента теплоотдачи при свободной конвекции основаны на экспериментальных исследованиях.
Конвективный теплообмен при свободном течении жидкости основан на изменении плотности жидкости при нагревании. В промышленности свободная конвекция широко применяется. Свободная конвекция возникает у нагретых стен котельных агрегатов, печей, батарей отопления, в холодильниках при охлаждении продуктов и т.д.
Если тело имеет более высокую температуру, чем окружающая среда, то слои жидкости, нагреваясь от тела, становятся легче и под действием подъемной силы поднимаются вверх, а на их место приходят более холодные слои. Поэтому возникает свободная конвекция.
Свободное движение жидкости у поверхности тела может быть как ламинарным, так и турбулентным. Характер движения жидкости в основном зависит от температурного напора, т.е. от разности температур стенки объекта и окружающей среды. При малых значениях температурного напора вдоль поверхности наблюдается ламинарное течение.
При больших температурных напорах преобладает турбулентное течение жидкости.
При свободной конвекции форма тела имеет второстепенное значение. Основное значение при свободной конвекции имеет длина поверхности, вдоль которой происходит теплообмен.
При свободной конвекции для определения средних значений коэффициентов теплоотдачи можно пользоваться формулами
При tст = соnst Nuж = 0,63 ( GrPr )0,25 2.63
При qст = const Nuж = 0,75 (Grж Prж)0,25 ( Prж / Prст)0,25 2.64
Формулы получены для теплоносителей с числом Рr от 0.7 до 3.103 при103 < Gr Pr < 109.
За определяющую температуру принята температура вдали от нагретой поверхности, за определяющий размер – длина поверхности.
Для определения средних значений коэффициентов теплоотдачи при свободном турбулентном течении жидкости вдоль вертикальной стенки, которое наступает при числах Grж Prж > 6.1010 предложена формула
Nuж = 0,15 ( Grж Prж )0,33( Prж/ Prcт)0,25 2.65
Если 109 < GrжPrж < 6.1010, то вдоль вертикальной пластины имеет место переходный режим свободного движения жидкости. Переходный процесс характеризуется неустойчивостью как процесса течения жидкости, так и теплоотдачи.
Для определения средних коэффициентов теплоотдачи при свободном ламинарном движении жидкости около горизонтальных труб при 103 < GrжPrж < 108 предложена формула
Nuж = 0,5 ( Grж Prж )0,23( Рrж / Рrст )0,25 2.66
В этой формуле за определяющую температуру принята температура капельной жидкости или газа вдали от трубы, а за определяющий размер – диаметр трубы. Около горизонтальных нагретых поверхностей движение жидкости имеет особый характер и зависит от положения и размеров теплоотдающих поверхностей. Если нагретая поверхность обращена кверху, то коэффициент теплоотдачи увеличивается на 30%. Если поверхность обращена книзу, то коэффициент теплоотдачи уменьшается на 30%. При расчете теплоотдачи плит за определяющий размер берется меньшая сторона плиты.
Теплоотдача в ограниченном пространстве при свободном движении жидкости представляет более сложную картину и рассматривается в специальной литературе.
3. ТЕПЛООБМЕН ПРИ ИЗМЕНЕНИИ АГРЕГАТНОГО СОСТОЯНИЯ ВЕЩЕСТВА.
Изменение агрегатного состояния вещества происходит при кипении и конденсации.
Кипение возможно во всем температурном интервале между тройной и критическими точками для данного вещества. Характерной особенностью процесса кипения является образование пузырьков пара. В процессе фазового превращения поглощается теплота парообразования. Процесс кипения всегда связан с подводом теплоты к кипящей системе.
Различают кипение жидкости на твердой поверхности и кипение в объеме жидкости.
Процесс кипения на твердой поверхности возникает тогда, когда температура жидкости выше температуры насыщения при данном давлении, а температура поверхности теплообмена выше температуры кипящей жидкости. Образование пузырьков пара происходит непосредственно на поверхности теплообмена.
Объемное кипение возникает при перегреве жидкости относительно температуры насыщения при данном давлении. Объемное кипение можно получить при быстром уменьшении давления или при наличии в жидкости внутренних источников теплоты.
Следует обращать внимание на особенности кипения в большом объеме, при кипении на пучках труб, при кипении внутри труб, при кипении в стекающей пленке.
Наиболее простым является пузырьковое кипение в большом объеме, при котором образующийся пар свободно удаляется от поверхности нагрева.
Около нагреваемой поверхности при кипении образуется тонкий пограничный слой, в котором жидкость перегрета на ∆t = tcт – tж. Для пара температура насыщения при нормальном атмосферном давлении t0 = 1000C, температура всей массы жидкости равна 100,40С, а температура пограничного слоя 109,10С.
Пузырьки пара зарождаются на обогреваемой поверхности в перегретом пограничном слое жидкости и только в отдельных точках, называемых центрами парообразования.
Количество пузырьков пара будет тем больше, чем больше тепловая нагрузка поверхности нагрева, чем больше температурный напор, чем грязнее поверхность. Размер пузырьков пара зависит от смачивающей способности жидкости. При хорошей смачиваемости пузырек пара имеет тонкую ножку и легко отрывается от поверхности. При плохой смачиваемости пузырек имеет толстую ножку и трудно отрывается. Отрыв пузырьков пара вызывает интенсивную циркуляцию и перемешивание, вследствие чего резко увеличивается интенсивность теплоотдачи. Такой режим называют пузырьковым кипением.
С возрастанием температурного напора количество пузырьков увеличивается и их становится так много, что они сливаются в сплошную пленку, которая периодически разрывается и пар прорывается в объем жидкости. Такой режим кипения называется пленочным.
Ввиду малой теплопроводности пара пленка создает большое термическое сопротивление, теплоотдача резко падает, а температура в пограничном слое резко возрастает, что может привести к пережогу труб, к аварии.
При кипении жидкости в большом объеме в условиях свободного движения коэффициент теплоотдачи зависит от физических свойств жидкости, температурного напора и давления.
При малых температурных напорах – до 50 – значение
коэффициента теплоотдачи определяется условиями свободной конвекции однофазной жидкости. При увеличении ∆t коэффициент теплоотдачи быстро возрастает и происходит интенсивное пузырьковое кипение. Рис.2.7.
В точке К (рис.2.7) наступает изменение режима кипения пузырьковое кипение переходит в пленочное, коэффициент теплоотдачи падает.
На приведенном рисунке показан график изменения коэффициента теплоотдачи при кипении и зависимость поверхностной плотности теплового потока от ∆t.
Значения ∆t,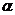 
, q, соответствующие моменту перехода пузырькового режима кипения в пленочное, называется критическим. Нахождение этих величин имеет большое практическое значение для выбора оптимального режима работы выпарных и кипятильных аппаратов.
На основании теории подобия для определения коэффициента теплоотдачи и критического значения теплового потока при пузырьковом кипении жидкости в условиях естественной конвекции в большом объеме предложены формулы
2.67
2.68
где ρ/ и ρ// - плотности жидкости и газа, кг / м3; r – теплота парообразования, кДж/кг;
б – коэффициент поверхностного натяжения, кг/м; λ – теплопроводность жидкости, Вт/м К
μ- динамическая вязкость жидкости; с- теплоемкость жидкости, кДж/ (кг К); Т – абсолютная температура насыщенного пара при данном давлении, К.
Академик М.А.Михеев рекомендует для р = 0,02 – 8,0 Мпа при пузырьковом кипении воды формулу
α =4,45 р0,15 q0,7 2.69
а = 146,1Δt2,33р0,5 2.70
где Δt = t ст – tж – температурный напор, К; р – абсолютное давление пара, МПа; q – поверхностная плотность теплового потока.
Конденсация, т.е. переход пара в жидкое состояние возможен только при условии, что температура и давление пара ниже температуры и давления критической точки.
Конденсация протекает как в объеме пара, так и на твердых охлаждаемых поверхностях.
В зависимости от состояния поверхности различают конденсацию пленочную и капельную. На жирной поверхности (покрытой жирными веществами) может происходить только капельная конденсация. Капельная конденсация для водяного пара явление случайное, неустойчивое. При капельной конденсации интенсивность теплоотдачи в 15 – 20 раз выше пленочной. С помощью лиофобизаторов или гидрофобизаторов создают искусственную капельную конденсацию
Следует различать конденсацию для вертикальной и горизонтальной стенки.
Для вертикальной стенки:
2.71
Для горизонтальной стенки
2.72
Где g – ускорение свободного падения; λж – теплопроводность жидкости; ρж – плотность жидкости; νж –кинематическая вязкость жидкости; ґ – теплота прарообразования; Н – высота вертикальной стенки; d – наружный диаметр трубы.
Физические параметры конденсата берутся по средней температуре пленки конденсата tср = 0,5 (tн+ tст), теплота парообразования берется по температуре насыщения tн .
Масса конденсата, образующегося на 1 м2 поверхности определяется по формуле
m = q /ґ = ( λ / δг ) (tн – tст ) 2.73
Размерность массы конденсата – кг / (с м2 )
При скорости конденсата < 10 м/с при совпадении движения пленки конденсата и движении пара, толщина пленки уменьшается, коэффициент теплоотдачи увеличивается.
При встречном движении пара и пленки конденсата коэффициент теплоотдачи уменьшается, а толщина пленки увеличивается. Толщина пленки конденсата на чистой поверхности на 30 % меньше толщины пленки на ржавой поверхности.
Примеси газов в паре уменьшают теплоотдачу при конденсации. Наличие в паре 1%
Воздуха уменьшает коэффициент теплоотдачи при конденсации на 60%.
Расположение труб конденсатора также влияет на процесс конденсации.
ТЕПЛОПЕРЕДАЧА
Теплопередачей называется передача теплоты от одной подвижной среды (жидкости или газа) к другой через разделяющую их однородную или многослойную твердую стенку любой формы. Теплопередача (сложный теплообмен) включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной жидкости. При интенсивной теплоотдаче тепловое излучение часто не учитывается.
Приведем рассмотренные ранее уравнения. Для теплоотдачи q = α1(t ж1 – tст1). Для теплопроводности плоской однослойной стенки q = λ ( tст1 – tст2 ) / δ, уравнение теплоотдачи q = ά2 ( t ст2 – t ж2 )
Рис.2.8. Распределение температур в процессе теплопередачи в плоской стенки
Суммируя полученные уравнения, получим
q = ( t ж1 – t ж2 ) / ( 1/ α1 +δ / λ + 1 / α2 ) 2. 74
где 1/α1 - частное термическое сопротивление в процессе теплоотдачи от горячей жидкости к стенке; 1/α2 - частное термическое сопротивление в процессе теплоотдачи от стенки к холодной жидкости; δ / λ - частное термическое сопротивление в процессе теплопроводности в стенке
R1 + R2 + R3 = R 2.75
Где R - полное термическое сопротивление в процессе теплопередачи.
1/R = k, 2.76
где k - коэффициент теплопередачи, Вт / ( м2 К ).
Уравнение теплопередачи имеет вид
Q = k ( t ж1 – t ж2 )F = k ∆t F 2. 77
Дата добавления: 2018-05-12; просмотров: 419; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!