Модель матрицы доступов Харрисона-Руззо-Ульмана (Пример Дискреционной политики безопансоти).
Модель Харрисона–Руззо–Ульмана (HRU) разработана и впервые предложена в 1971 г., а в 1976 г. появилось ее формальное описание. Она используется для анализа системы защиты, реализующей дискреционную политику безопасности, и ее основного элемента – матрицы доступов. При этом система защиты представляется конечным автоматом, функционирующим согласно определенным правилам перехода.
Обозначим: O – множество объектов системы; S – множество субъектов системы (S≤ O); R – множество прав доступа субъектов к объектам, например права на чтение (read), на запись (write), владения (own); M – матрица доступа, строки которой соответствуют субъектам, а столбцы – объектам; M[s, о] ≤ R – права доступа субъекта s к объекту о. Отдельный автомат, построенный согласно положениям модели HRU, будем называть системой. Функционирование системы рассматривается только с точки зрения изменений в матрице доступа. Возможные изменения определяются шестью примитивными операторами:
«Внести» право r 
R в M[s, о] – добавление субъекту s права доступа r к объекту о.При этом в ячейку M[s, о] матрицы доступов добавляется элемент r.
«Удалить» право r R из M[s, о] – удаление у субъекта s права доступа r к объекту о. При этом из ячейки M[s, о] матрицы доступов удаляется элемент r.
«Создать» субъект s' – добавление в систему нового субъекта s'. При этом в матрицу доступов добавляются новые столбец и строка.
«Создать» объект о' – добавление в систему нового объекта о'. При этом в матрицу доступов добавляется новый столбец.
|
|
|
«Уничтожить» субъект s' – удаление из системы субъекта s'. При этом из матрицы доступов удаляются соответствующие столбец и строка.
«Уничтожить» объект о' – удаление из системы объекта о'. При этом из матрицы доступов удаляется соответствующий столбец.
В результате выполнения примитивного оператора а осуществляется переход системы из состояния Q = (S, О, M) в новое состояние Q ' = (S ', O ', M ') (табл. 5.2). Данный переход обозначим через Q ├ α Q '.
Таблица 1Таблица переходов из состояния состояние модели HRU
Из примитивных операторов могут составляться команды. Каждая команда состоит из двух частей: условия, при котором выполняется команда, и последовательности примитивных операторов.
Модель системы безопасности Бэлла-Лападула (Пример мандатного разграничения доступа).
Классическая модель Белла–Лападула (БЛ) построена для анализа систем защиты, реализующих мандатное (полномочное) разграничение доступа. Модель БЛ была предложена в 1975 г.Пусть определены конечные множества: S – множество субъектов системы (например, пользователи системы и программы); О – множество объектов системы (например, все системные файлы); R = (read, write, append, execute) – множество видов доступа субъектов из S к объектам из О, где read – доступ на чтение, write – на запись, append – на запись в конец объекта, execute – на выполнение.
|
|
|
Обозначим:
В = {b 
S × O × R} – множество возможных множеств текущих доступов в системе;
М = sо М – матрица разрешенных доступов, где Мso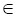 
R – разрешенный доступ
субъекта s к объекту о;
L – множество уровней секретности, например L = {U, С, S, TS}, где U < С < S < TS;
(fs, fo, fc) 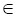F = Ls × Lo× Lc – тройка функций (fs, fo, fc), определяющих:
fs : S → L – уровень допуска субъекта;
fo : S → L – уровень секретности объекта;
fc : S → L – текущий уровень допуска субъекта, при этом 
s 
Sfc(s) ≤ fs(s);
Н – текущий уровень иерархии объектов;
V = В × М × F × Н – множество состояний системы;
Q – множество запросов системе;
D – множество решений по запросам, например {уеs, по, error};
W 
Q × D × V × V – множество действий системы, где четверка (q, d, v2, v1) W оз-
начает, что система по запросу q с ответом d перешла из состояния v1 в состояние v2;
No – множество значений времени {No = 0, 1, 2, ...};
Х – множество функций x: No → Q, задающих все возможные последовательности запросов к системе;
|
|
|
Y – множество функций у: No → D, задающих все возможные последовательности ответов системы по запросам;
Z – множество функций z: No → V, задающих все возможные последовательности состояний системы.
Безопасность системы определяется с помощью трех свойств:
ss – свойства простой безопасности (simple security);
*– свойства звезды;
ds – свойства дискретной безопасности (discretionary security).
Оперируя этими свойствами и их сочетаниями возможно построение защиты систе-
мы любой сложности.
Дата добавления: 2018-05-12; просмотров: 1540; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!