Алгоритмы формирования псевдослучайных чисел.

⇐ ПредыдущаяСтр 8 из 25Следующая ⇒

Данные алгоритмы являются рекуррентными, т.е. формируют следующие числа через предыдущие, а самое 1-ое число определяется начальным состоянием.

Метод Фон-Неймана.

А₁ – 1-ое начальное состояние.

Береться произвольное четырехразрядное число, чтобы сформировать следующее число А_i₊₁, через А_i, А_i возводят в квадрат в качестве А_{i+1 ,}берут средние четыре цифры.

А_i =1204 А_i²=1459616 А_i+1=4596.

Недостаток – в некторых случаях алгоритм вырождается и начинает формировать одни и те же числа с маленьким периодом. Период ГПСЧ – величина отрезка на котором формируемые числа не повторяются.

Конгруэнтные датчики ПСП

В настоящее время наиболее доступными и эффективными являются конгруэнтные генераторы ПСП. Для этого класса генераторов можно сделать математически строгое заключение о том, какими свойствами обладают выходные сигналы этих генераторов с точки зрения периодичности и случайности.

Одним из хороших конгруэнтных генераторов является линейный конгруэнтный датчик ПСЧ. Он вырабатывает последовательности псевдослучайных чисел T(i), описываемые соотношением

T(i+1) = (A*T(i)+C)mod m,

где А и С - константы, Т(0) - исходная величина, выбранная в качестве порождающего числа. Очевидно, что эти три величины и образуют ключ.

Такой датчик ПСЧ генерирует псевдослучайные числа с определенным периодом повторения, зависящим от выбранных значений А и С. Значение m обычно устанавливается равным 2n , где n - длина машинного слова в битах. Датчик имеет максимальный период М до того, как генерируемая последовательность начнет повторяться. По причине, отмеченной ранее, необходимо выбирать числа А и С такие, чтобы период М был максимальным. Как показано Д. Кнутом, линейный конгруэнтный датчик ПСЧ имеет максимальную длину М тогда и только тогда, когда С - нечетное, и Аmod 4 = 1.

Для шифрования данных с помощью датчика ПСЧ может быть выбран ключ любого размера. Например, пусть ключ состоит из набора чисел x(j) размерностью b, где j=1, 2, ..., n. Тогда создаваемую гамму шифра G можно представить как объединение непересекающихся множеств H(j).

Требования к ГПСЧ.

1. Большой период.

2. Равномерность распределения.

3. Непредсказуемость.

Требования к стойким алгоритмам шифрования:

1. Зашифрованный текст должен поддаваться чтению только при наличии ключа шифрования. Для взлома стойких шифров должен проходить только один метод криптоанализа – полный перебор ключей.

2. Знание алгоритма шифрования не должно влиять на надежность защиты.

3. Если злоумышленнику стал доступен весь открытый текст и результат его шифрования, то для нахождения ключа шифрования все равно требуется полный перебор ключей (Невозможность атаки по открытому тексту).

4. Незначительное изменение открытого текста должно приводить к значительному изменению закрытого текста.

5. Незначительное изменение ключа должно приводить к существенному изменению закрытого текста.

4.4.6 Стандарт шифрования данных ГОСТ 28147-89[1].

Он рекомендован к использованию для защиты любых данных, представленных в виде двоичного кода, хотя не исключаются и другие методы шифрования. Данный стандарт формировался с учетом мирового опыта, и в частности, были приняты во внимание недостатки и нереализованные возможности алгоритма DES, поэтому использование стандарта ГОСТ предпочтительнее. Алгоритм достаточно сложен и ниже будет описана в основном его концепция.

Введем ассоциативную операцию конкатенации, используя для нее мультипликативную запись. Кроме того будем использовать следующие операции сложения:

· AÅB - побитовое сложение по модулю 2;

· A[+]B - сложение по модулю 2³²;

· A{+}B - сложение по модулю 2³²-1;.

Алгоритм криптографического преобразования предусматривает несколько режимов работы. Во всех режимах используется ключ W длиной 256 бит, представляемый в виде восьми 32-разрядных чисел x(i).

W=X(7)X(6)X(5)X(4)X(3)X(2)X(1)X(0)

Для дешифрования используется тот же ключ, но процесс дешифрования является инверсным по отношению к исходному.

Самый простой из возможных режимов - замена.

Пусть открытые блоки разбиты на блоки по 64 бит в каждом, которые обозначим как T(j).

Очередная последовательность бит T(j) разделяется на две последовательности B(0) и A(0) по 32 бита (правый и левый блоки). Далее выполняется итеративный процесс шифрования описываемый следующими формулами, вид который зависит от :i:

· Для i=1, 2, ..., 24, j=(i-1)mod 8;

A(i) = f(A(i-1) [+] x(j)) Å B(i-1)

B(i) = A(i-1)

· Для i=25, 26, ..., 31, j=32-i;

A(i) = f(A(i-1) [+] x(j)) Å B(i-1)

B(i) = A(i-1)

· Для i=32

A(32) = A(31)

B(32) = f(A(31) [+] x(0)) Å B(31).

Здесь i обозначает номер итерации. Функция f – функция шифрования.

Функция шифрования включает две операции над 32-разрядным аргументом.

Первая операция является подстановкой K. Блок подстановки К состоит из 8 узлов замены К(1)...К(8) с памятью 64 бита каждый. Поступающий на блок подстановки 32-разрядный вектор разбивается на 8 последовательно идущих 4-разрядных вектора, каждый из который преобразуется в 4-разрядный вектор соответствующим узлом замены, представляющим из себя таблицу из 16 целых чисел в диапазоне 0...15. Входной вектор определяет адрес строки в таблице, число из которой является выходным вектором. Затем 4-разрядные векторы последовательно объединяются в 32-разрядный выходной.

Вторая операция - циклический сдвиг влево 32-разрядного вектора, полученного в результате подстановки К. 64-разрядный блок зашифрованных данных Т представляется в виде

Т=А(32)В(32).

Остальные блоки открытых данных в режиме простой замены зашифровываются аналогично.

Следует учитывать, что данный режим шифрования обладает ограниченной криптостойкостью.

Другой режим шифрования называется режимом гаммирования.

Открытые данные, разбитые на 64-разрядные блоки T(i) (i=1,2,...,m) (m определяется объемом шифруемых данных), зашифровываются в режиме гаммирования путем поразрядного сложения по модулю 2 с гаммой шифра Г_ш, которая вырабатывается блоками по 64 бит, т.е.

Г_ш=(Г(1),Г(2),....,Г(m)).

Уравнение шифрования данных в режиме гаммирования может быть представлено в следующем виде:

Ш(i)=A(Y(i-1) Å C2, Z(i-1)) {+} C(1) Å T(i)=Г(i) Å T(i)

В этом уравнении Ш(i) обозначает 64-разрядный блок зашифрованного текста, А - функцию шифрования в режиме простой замены (аргументами этой функции являются два 32-разрядных числа). С1 и С2 - константы, заданные в ГОСТ 28147-89. Величины y(i) и Z(i) определяются итерационно по мере формирования гаммы следующим образом:

(Y(0),Z(0))=A(S), S - 64-разрядная двоичная последовательность

(Y(i),Z(i))=(Y(i-1) [+] C2, Z(i-1) {+} C(1)), i=1, 2, ..., m.

64-разрядная последовательность, называемая синхропосылкой, не является секретным элементом шифра, но ее наличие необходимо как на передающей стороне, так и на приемной.

Режим гаммирования с обратной связью очень похож на режим гаммирования. Как и в режиме гаммирования открытые данные, разбитые на 64-разрядные блоки T(i), зашифровываются путем поразрядного сложения по модулю 2 с гаммой шифра Г_ш, которая вырабатывается блоками по 64 бит:

Г_ш=(Г(1), Г(2), ..., Г(m)).

Уравнение шифрования данных в режиме гаммирования с обратной связью выглядят следующим образом:

Ш(1)=A(S)ÅT(1)=Г(1)ÅT(1),

Ш(i)=A(Ш(i-1)ÅT(i)=Г(i)ÅT(i), i=2, 3, ..., m.

В ГОСТ 28147-89 определяется процесс выработки имитовставки, который единообразен для всех режимов шифрования. Имитовставка - это блок из р бит (имитовставка И_р), который вырабатывается либо перед шифрованием всего сообщения. либо параллельно с шифрованием по блокам. Параметр р выбирается в соответствии с необходимым уровнем имитозащищенности.

Для получения имитовставки открытые данные представляются также в виде блоков по 64 бит. Первый блок открытых данных Т(1) подвергается преобразованию, соответствующему первым 16 циклам алгоритма режима простой замены. Причем в качестве ключа используется тот же ключ, что и для шифрования данных. Полученное 64-разрядно число суммируется с открытым блоком Т(2) и сумма вновь подвергается 16 циклам шифрования для режима простой замены. Данная процедура повторятся для всех m блоков сообщения. Из полученного 64-разрядного числа выбирается отрезок И_р длиной р бит.

Имитовставка передается по каналу связи после зашифрованных данных. На приемной стороне аналогичным образом из принятого сообщения выделяется? имитовставка и сравнивается с полученной откуда?. В случае несовпадения имитовставок сообщение считается ложным.

Шифр Rijndael.

Данный алгоритм разработан двумя специалистами по криптографии из Бельгии. Он является нетрадиционным блочным шифром, поскольку не использует сеть Фейштеля для криптопреобразований. Алгоритм представляет каждый блок кодируемых данных в виде двумерного массива байт размером 4х4, 4х6 или 4х8 в зависимости от установленной длины блока. Далее на соответствующих этапах преобразования производятся либо над независимыми столбцами, либо над независимыми строками, либо вообще над отдельными байтами в таблице.

Все преобразования в шифре имеют строгое математическое обоснование. Сама структура и последовательность операций позволяют выполнять данный алгоритм эффективно как на 8-битных так и на 32-битных процессорах. В структуре алгоритма заложена возможность параллельного исполнения некоторых операций, что на многопроцессорных рабочих станциях может еще поднять скорость шифрования в 4 раза.

Алгоритм состоит из некоторого количества раундов (от 10 до 14 – это зависит от размера блока и длины ключа), в которых последовательно выполняются следующие операции :

ByteSub – табличная подстановка 8х8 бит (рис.1),

Рис.1.

ShiftRow – сдвиг строк в двумерном массиве на различные смещения (рис.2),

Рис.2.

MixColumn – математическое преобразование, перемешивающее данные внутри столбца (рис.3),

Рис.3.

AddRoundKey – добавление материала ключа операцией XOR (рис.4).

Рис.4.

В последнем раунде операция перемешивания столбцов отсутствует, что делает всю последовательность операций симметричной. Соответственно для него ещё присутствуют методы расширения материала ключа, методы создания таблицы подстановок (S'box-ов), но размер лекций не позволяют нам рассмотреть эти моменты.

Ассиметричные криптосистемы.

Слабостью симметричных криптосистем является процедура распределения ключа. Ассиметричные криптосистемы характеризуются тем что в них для шифрования и расшифрования используются разные ключи, связанные между собой некоторой математической зависимостью. При этом данная зависимость такова, что зная один из ключей вычислить другой очень трудно. В зависимости от того для чего именно используется криптосистема один из ключей является общедоступным, если криптосистема используется для шифрования передаваемых сообщении, общедоступным будет ключ на основе которого шифруется сообщение, а ключ расшифрования будет секретным, если же наоборот сделать общедоступным ключ расшифрования, то можно построить систему проверки подлинности сообщении (ЭЦП).

Шифратор

Дешифратор

Открытый Ключ (k1)

Закрытый Ключ (k2)

Отправитель (А)

Получатель (В)

Исходное сообщение (X)

Зашифрованное сообщение Y=E_k₁(X)

X=D_k2(E_k1(X))

Криптосистема с открытым ключом определяется тремя алгоритмами: генерация ключей, шифрования и расшифрования. Алгоритм генерации ключей открыт, всякий может подать ему на вход случайную строку r надлежащей длины и получить пару ключей (k_1,k₂). Один из ключей (например k₁) публикуется, он называется открытым, а второй, называемый секретным, хранится в тайне. Алгоритм шифрования E_k₁ и расшифрования D_k₂ таковы, что для любого открытого текста m выполняется D_k₂(E_k₁(m))=m.

Криптографические системы с открытым ключом используют так называемые необратимые или односторонние функции, которые обладают следующим свойством: при заданном значении x относительно просто вычислить значение f(x), однако если y=f(x), то нет простого пути для вычисления значения x.

Множество классов необратимых функций и порождает все разнообразие систем с открытым ключом. Однако не всякая необратимая функция годится для использования в реальных ИС.

В самом определении необратимости присутствует неопределенность. Под необратимостью понимается не теоретическая необратимость, а практическая невозможность вычислить обратное значение используя современные вычислительные средства за обозримый интервал времени.

Алгоритм шифрования с открытым ключом:

Шифратор

Дешифратор

Открытый Ключ (kU_b)

Закрытый Ключ (kR_b)

Отправитель (А)

Получатель (В)

Исходное сообщение (X)

Зашифрованное сообщение Y=E_k₁(X)

X=D_k2(E_k1(X))

Пользователь В создает пару ключей kU_b и kR_b, используемых для шифрования и дешифрования передаваемых сообщений.
Пользователь В делает доступным некоторым надежным способом свой ключ шифрования, т.е. открытый ключ kU_b. Составляющий пару закрытый ключ KR_b держится в секрете.
Если А хочет послать сообщение В, он шифрует сообщение, используя открытый ключ В KU_b .
Когда В получает сообщение, он дешифрует его, используя свой закрытый ключ KR_b. Никто другой не сможет дешифровать сообщение, так как этот закрытый ключ знает только В.

Если пользователь (конечная система) надежно хранит свой закрытый ключ, никто не сможет подсмотреть передаваемые сообщения.

Создание и проверка подписи состоит из следующих шагов:

Создание подписи (Шифратор)

Проверка подписи (Дешифратор)

Открытый Ключ (kU_a)

Закрытый Ключ (kR_a)

Отправитель (А)

Получатель (В)

Исходное сообщение (X)

Зашифрованное сообщение Y=E_k₁(X)

X=D_k2(E_k1(X))

Пользователь А создает пару ключей kR_A и kU_A, используемых для создания и проверки подписи передаваемых сообщений.
Пользователь А делает доступным некоторым надежным способом свой ключ проверки, т.е. открытый ключ kU_A. Составляющий пару закрытый ключ kR_A держится в секрете.
Если А хочет послать подписанное сообщение В, он создает подпись E_KRa[M] для этого сообщения, используя свой закрытый ключ kR_A.
Когда В получает подписанное сообщение, он проверяет подпись D_KUa[M], используя открытый ключ А kU_A. Никто другой не может подписать сообщение, так как этот закрытый ключ знает только А.

До тех пор, пока пользователь или прикладная система надежно хранит свой закрытый ключ, их подписи достоверны.

Кроме того, невозможно изменить сообщение, не имея доступа к закрытому ключу А; тем самым обеспечивается аутентификация и целостность данных.

В этой схеме все сообщение подписывается, причем для подтверждения целостности сообщения требуется много памяти. Каждое сообщение должно храниться в незашифрованном виде для использования в практических целях. Кроме того, копия сообщения также должна храниться в зашифрованном виде, чтобы можно было проверить в случае необходимости подпись. Более эффективным способом является шифрование небольшого блока битов, который является функцией от сообщения. Такой блок, называемый аутентификатором, должен обладать свойством невозможности изменения сообщения без изменения аутентификатора. Если аутентификатор зашифрован закрытым ключом отправителя, он является цифровой подписью, с помощью которой можно проверить исходное сообщение. Далее эта технология будет рассматриваться в деталях.

4.5.1 Алгоритм RSA.

Генерация ключа.

1. Выбираются два простых числа p и q.

Простое число - это число, которое делится только на себя (без остатка).

Взаимно простые числа - несколько целых чисел, таких, что общими делителями для всех этих чисел являются лишь + 1 и - 1.

2. Вычисляется их произведение n=p*q

3. Выбирается произвольное число e (e<n), такое что НОД(e, (p-1)(q-1))=1, т.е. другими словами e должно быть взаимно простым числом с (p-1)(q-1).

4. Методом Евклида решается в целых числах уравнение e*d+(p-1)(q-1)*y=1. Здесь неизвестными являются d и y – метод Евклида как раз находит множество пар (d,y), каждая из которых является решением уравнения в целых числах.

5. Два числа (e,n) – публикуются как открытый ключ. (d,n) – закрытый ключ.

Шифрование.

1. Отправитель разбивает свое сообщение на блоки, равные k=[log₂(n)] бит, где квадратные скобки обозначают взятие целой части от дробного числа.

2. Подобный блок, интерпритируется как число из диапазона (0;2^k-1). Для каждого такого числа (назовем его m_i) вычисляется выражение с_i=((m_i)^e)mod n. Блоки с_i и есть зашифрованное сообщение.

Расшифрование.

((с_i)^d)mod n = m_i

Согласно теореме Эйлера, частный случай которой утверждает, что если число n представимо в виде двух простых чисел p и q, то для любого x имеет место равенство

(x⁽^p^-1)(^q^-1)) mod n=1

Для дешифрования RSA сообщения воспользуемся этой формулой.

Возведем обе её части в степень (-y): (x^(-^y⁾⁽^p^-1)(^q^-1))mod n=1^(-^y⁾=1

Теперь умножим обе её части на x: (x^(-^y⁾⁽^p^-1)(^q^-1)+1)mod n= x

А теперь вспомним как мы подбирали с помощью алгоритма Евклида d такое, что e*d+(p-1)(q-1)*y=1, т.е. e*d=(-y)(p-1)(q-1)+1.

Получим:

(x^e^*^d) mod n = x

Т.е. для того чтобы прочесть сообщение с_i=((m_i)^e)mod n, достаточно возвести его в степень d по модулю m:

((с_i)^d)mod n = ((m_i)^e*d)mod n = m_i

Замечание: На самом деле процесс возведения в степень достаточно трудоемок даже для современных процессоров. Поэтому весь текст сообщения обычно кодируется обычным блочным шифром, но с использованием ключа сеанса, а вот сам ключ сеанса шифруется как раз ассиметричным алгоритмом, с помощью открытого ключа получателя.

Пример Зашифруем сообщение “САВ”. Для простоты будем использовать маленькие числа (на практике применяются гораздо большие).

1. Выберем p=3 и q=11.

2. Определим n=3*11=33.

3. Найдем (p-1)(q-1)=20. Следовательно, в качестве d, взаимно простое с 20, например, d=3.

4. Выберем число е. В качестве такого числа может быть взято любое число, для которого удовлетворяется соотношение (е*3) (mod 20) = 1, например 7.

5. Представим шифруемое сообщение как последовательность целых чисел с помощью отображения: А®1, В®2, С®3. Тогда сообщение принимает вид (3,1,2). Зашифруем сообщение с помощью ключа {7,33}.

ШТ1 = (3⁷) (mod 33) = 2187 (mod 33) = 9,

ШТ2 = (1⁷) (mod 33) = 1 (mod 33) = 1,

ШТ3 = (2⁷) (mod 33) = 128 (mod 33) = 29.

6. Расшифруем полученное зашифрованное сообщение (9,1,29) на основе закрытого ключа {3,33}:

ИТ1 = (9³) (mod 33) = 729 (mod 33) = 3,

ИТ2= (1³) (mod 33) = 1 (mod 33) = 1,

ИТ3 = (29³) (mod 33) = 24389 (mod 33) = 2.

4.5.2. Алгоритм Эль-Гамаля.

Данная система является альтернативой RSA и при равном значении ключа обеспечивает ту же криптостойкость .

Протокол передачи выглядит следующим образом:

1. Пользователям извеcтны числа P и G, первое из которых «большое простое число», насчитывающее около 1024 битов, такое что p-1 делится на другое «среднее простое число» Q, а второе – целое, причем

G⁽^P^-¹^)/^Q(mod P) ≠ 1.

2. После выбора параметров домена определяют открытый и секретный ключи. Секретным ключом может быть любое натуральное число x, а открытый ключ получается по следующей формуле:

H = G^x mod P.

3. Для шифрования поступают следующим образом:

- генерируют случайный эфемерный ключ k;

- вычисляют C₁ = G^k;

- находят С₂ = m * H^k,

- выдают получившийся шифротекст в виде пары С = (C₁, С₂).

Криптографический ключ называется эфемерным, если он создан специально для выполнения только одного распределения ключей.

Чтобы расшифровать пару данных С = (C₁, C₂), производят следующие преобразования:

Разберем небольшой пример, выбрав сначала параметры домена.

Пусть Q = 101, Р = 809 и G = 3.

Легко проверить, что Q действительно делит число Р — 1, а порядок элемента G в группе Fp делится на Q, Порядок элемента G равен 808, поскольку

3⁸⁰⁸ (mod P) = 1;

И ни при каких меньших степенях такого равенства не получается.

В качестве пары открытого и секретного ключа выберем

x= 68 и H = G^x = 3⁶⁸ = 65 (mod P).

Допустим, нам нужно зашифровать сообщение, численное представление которого равно m = 100. Поступаем следующим образом.

- Генерируем случайный эфемерный ключ k = 89,

- Находим C₁= G^k = 3⁸⁹ = 345 (mod P).

- Получаем C₂ = m * H^k =100 • 65⁸⁹ = 517 (modP).

- Отправляем шифротекст С = (345,517).

Партнер сможет восстановить текст, делая также вычисления:

Хэш-функции.

Хеш-функция — функция, выполняющая одностороннее преобразование входных данных, называемая также хешированием.

Хеширование – это преобразование входного массива данных произвольной длины в выходную битовую строку фиксированной длины таким образом, чтобы изменение входных данных приводило к непредсказуемому изменению выходных данных. Такие преобразования также называются функциями свёртки, а их результаты называют хешем, хеш-кодом или дайджестом сообщения (англ. message digest).

В общем случае однозначного соответствия между исходными данными и хеш-кодом быть не может. Существует множество массивов данных, дающих одинаковые хеш-коды (так называемые коллизии), и каждая хэш-функция должна оцениваться по стойкости к возникновению коллизий.

Простым примером хеширования может служить нахождение контрольной суммы сообщения.

Криптографическая хеш-функция должна обеспечивать:

· стойкость к коллизиям (два различных набора данных должны иметь различные результаты преобразования)

· необратимость (невозможность вычислить исходные данные по результату преобразования)

(Для специальностей 230101 Можно привести алгоритм MD5)

ЭЦП

Электро́нная цифрова́я по́дпись (ЭЦП)— реквизит ( - элементы документа, которые должны обязательно в нем присутствовать, иначе документ будет считаться недействительным) электронного документа.

Цели, преследуемые созданием ЭЦП:

1. Удостоверение источника документа. (получателю сообщения требуется убедиться, что оно исходит от конкретного отправителя). В зависимости от деталей определения документа могут быть подписаны такие поля, как «автор», «внесённые изменения», «метка времени» и т. д.

2. Защиту от изменений документа. При любом случайном или преднамеренном изменении документа (или подписи) изменится хэш, следовательно, подпись станет недействительной.

3. Невозможность отказа от авторства. Так как создать корректную подпись можно лишь, зная закрытый ключ, а он известен только владельцу, то владелец не может отказаться от своей подписи под документом.

4.7.1 Схемы ЭЦП

Схема 1.

Данная схема предполагает шифрование электронного документа (ЭД) на основе симметричных алгоритмов и предусматривает наличие в системе третьего лица (арбитра), пользующегося доверием участников обмена подписанными подобным образом электронными документами. Взаимодействие пользователей данной системой производится по следующей схеме:

Участник A зашифровывает сообщение на своем секретном ключе KA, знание которого разделено с арбитром, затем шифрованное сообщение передается арбитру с указанием адресата данного сообщения (информация, идентифицирующая адресата, передается также в зашифрованном виде).

Арбитр расшифровывает полученное сообщение на ключе КА, производит необходимые проверки и затем зашифровывает на секретном ключе участника B (KB). Далее зашифрованное сообщение посылается участнику B вместе с информацией, что оно пришло от участника A.

Авторизацией документа в данной схеме считается сам факт зашифрования ЭД секретным ключом и передача зашифрованного ЭД арбитру. На практике эта схема не получила широкого распространения.

Схема 2.

Фактом подписания документа в данной схеме является зашифрование документа на секретном ключе его отправителя. Здесь используются асимметричные алгоритмы шифрования.

Вторая схема используется довольно редко вследствие того, что длина ЭД может оказаться очень большой (шифрование асимметричным алгоритмом может оказаться неэффективным по времени), но в этом случае в принципе не требуется наличие третьей стороны, хотя она и может выступать в роли сертификационного органа открытых ключей пользователя.

Схема 3.

Наиболее распространенная схема ЭЦП использует зашифрование окончательного результата обработки ЭД хэш-функцией при помощи асимметричного алгоритма.

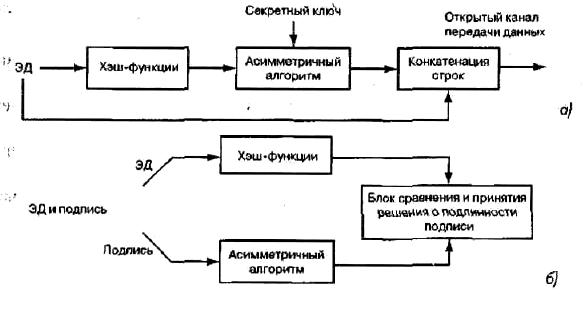
Генерация подписи происходит следующим образом.

Участник A вычисляет хэш-код от ЭД. Полученный хэш-код проходит процедуру преобразования с использованием своего секретного ключа. После чего полученное значение (которое и является ЭЦП) вместе с ЭД отправляется участнику B.

Участник B должен получить ЭД с ЭЦП и сертифицированный открытый ключ участника A, а затем произвести расшифрование на нем ЭЦП, сам ЭД подвергается операции хэширования, после чего результаты сравниваются, и если они совпадают, то ЭЦП признается истинной, в противном случае ложной.

В зависимости от алгоритма функция вычисления подписи может быть детерминированной или вероятностной. Детерминированные функции всегда вычисляют одинаковую подпись по одинаковым входным данным. Вероятностные функции вносят в подпись элемент случайности, что усиливает криптостойкость алгоритмов ЭЦП. Однако, для вероятностных схем необходим надёжный источник случайности (либо аппаратный генератор шума, либо криптографически надёжный генератор псевдослучайных бит), что усложняет реализацию.

4.7.2 Схема цифровой подписи на алгоритме RSA

Подпись сообщения вычисляется с использованием секретного ключа по формуле (обозначения используемые ранее):

Для проверки правильности подписи нужно убедиться, что выполняется равенство

Стеганография.

Стеганогра́фия (пер. с греч., «тайнопись») — это наука о скрытой передаче информации путём сохранения в тайне самого факта передачи. В отличие от криптографии, которая скрывает содержимое секретного сообщения, стеганография скрывает само его существование.

Классификация стеганографии

В конце 90-х годов выделилось несколько направлений стеганографии:

Классическая стеганография

Компьютерная стеганография

Цифровая стеганография

Классическая стеганография

Стеганография в Древнем мире

Существует версия, что древние шумеры одними из первых использовали стеганографию, так как было найдено множество глиняных клинописных табличек, в которых одна запись покрывалась слоем глины, а на втором слое писалась другая. Однако противники этой версии считают, что это было вовсе не попыткой скрытия информации, а всего лишь практической потребностью.

В трудах древнегреческого историка Геродота встречается описание еще двух методов сокрытия информации: на обритую голову раба записывалось необходимое сообщение, а когда его волосы отрастали, он отправлялся к адресату, который вновь брил его голову и считывал доставленное сообщение. Второй способ заключался в следующем: сообщение наносилось на деревянную дощечку, а потом она покрывалась воском, и, тем самым, не вызывала никаких подозрений. Потом воск соскабливался и сообщение становилось видимым.

Симпатические чернила

Одним из наиболее распространенных методов классической стеганографии является использование симпатических (невидимых) чернил. Текст, записанный такими чернилами, проявляется только при определенных условиях (нагрев, освещение, химический проявитель и т. д.) Изобретенные еще в в I веке н. э. Филоном Александрийским, они продолжали использоваться как в средневековье, так и в новейшее время, например, в письмах русских революционеров из тюрем.

Дата добавления: 2018-05-12; просмотров: 831; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒

Мы поможем в написании ваших работ!