Счетчик с групповым переносом
Для повышения быстродействия счетчиков с большим количеством разрядов применяют схемы с групповым переносом.
В схеме на рис. 2.64 принято, что внутри группы [1: К] разрядов перенос организован последовательным способом, а между группами – параллельным.

Рис. 2.64. Двоичный счетчик с групповым переносом
Полное количество разрядов в счетчике n =КL, где К – число разрядов в группе, L- количество групп.
τp – время формирования группового переноса или переноса между разрядами.
Время регистрации счетчика Трег = τp (K + L – 1).
Реверсивный счетчик
Реверсивный счетчик обеспечивает, как суммирование, так и вычитание импульсов из содержимого счетчика.
Существуют две основные структуры реверсивных счетчиков:
1) на вход схемы подается одна последовательность входных импульсов, но в каждый момент времени известен ее знак или режим работы счетчика,
2) на вход реверсивного счетчика поступают две последовательности импульсов с разными знаками.
Схема, представленная на рис. 2.65, соответствует первой структуре. На вход схемы поступает одна последовательность сигналов. Триггер знака ТЗн определяет режим работы счетчика.

 Рис. 2.65. Реверсивный счетчик
Рис. 2.65. Реверсивный счетчик
В режиме сложения формируется входной сигнал с положительным знаком и последовательность переносов
P0 ’:=‘ ТЗн * X0 ;
в режиме вычитания - последовательность заемов
Z0 ‘:=‘ IТЗн * X0 ;
|
|
|
таким образом, на входе первого триггера Q1 появляются две последовательности сигналов с разными знаками, что соответствует второй структуре. На рис. 2.65 показано УГО реверсивного счетчика этого типа.
Составим МОДИС-описание схемы счетчика, примем, что он состоит из восьми разрядов.
Q1 ‘:=‘ ‘ЕСЛИ’ Р0 V Z0 ‘ТО’ IQ1 ‘ИНАЧЕ’ Q1 ;
P1 ‘:=‘ Q1 * P0; Z  ‘:=’ IQ1 * Z
‘:=’ IQ1 * Z  ;
;
Q [1:8] ’:=‘ ‘ЕСЛИ’ ТЗн * X0 ‘ТО’ Q[1:8] + 1
‘ИНЕСЛИ’ IТЗн * X0 ‘ТО‘ Q[1:8] – 1
‘ИНАЧЕ’ Q [1:8];

Рис. 2.66. УГО реверсивного счетчика
Двоично-десятичные счетчики

Рис. 2.67. Обобщенная структура двоично-десятичного счетчика
Эти ФУ позволяют вести подсчет импульсов в десятичной системе счисления за счет использования различных двоично-десятичных кодов.
На рис. 2.67 представлена обобщенная структура двоично-десятичного счетчика.
Построение такого счетчика сводится к построению логической схемы одной декады в соответствии с выбранным двоично-десятичным кодом (табл.2.19).
Таблица 2.19
| № п/п | Веса разрядов | Наименование кода
| Сумма весов | |||
| 4 | 3 | 2 | 1 | |||
| 1 | 8 | 4 | 2 | 1 | 8421 | 15 |
| 2 | 5 | 2 | 1 | 1 | 5211 | 9 |
| 3 | 4 | 3 | 1 | 1 | 4221 | 9 |
| 4 | 3 | 3 | 2 | 1 | 3321 | 9 |
Рассмотрим пример построения логической схемы одной двоично-десятичной декады для кода 5211(табл.2.20).Пользуясь этой таблицей , можно составить МОДИС- описание схемы для одной декады при коде 5211.
|
|
|
ТГ1 ’:=‘ ‘ЕСЛИ’ IТГ1 * IТГ2 * IТГ3 * Р0 ‘ТО’ 1 ‘ИНЕСЛИ’ ТГ1 * ТГ2 * ТГ3 * Р0 ‘ТО’ 0 ‘ИНАЧЕ’ ТГ1;
ТГ4 ’:=‘ ‘ЕСЛИ’ IТГ4 * ТГ1 * ТГ2 * ТР3 * Р0 ’ТО’ 1 ‘ИНЕСЛИ’ ТГ4 * ТГ2 * ТГ3 * ТГ1 * Р0 ‘ТО’ 0 ‘ИНАЧЕ’ ТГ4;
Анализ условных предложений для ТГ1 и ТГ4 показывает, что они соответствуют триггеру типа R-S.
Работу ТГ4 можно описать иначе, как триггер со счетным входом.
ТГ4 ’:=’ ‘ЕСЛИ’ ТГ1 * ТГ2 * ТГ3 * Р0 ‘ТО’ IТГ4 ‘ИНАЧЕ’ ТГ4;
Таким же образом следует составить описание для остальных триггеров и схем формирования десятичных переносов.
Далее в соответствии с этими выражениями нужно построить логические схемы, управляемые триггерами и сами триггеры.
Таблица 2.20
Десятичная цифра | Двоично-десятичный код
ТГ4 ТГ3 ТГ2 ТГ1 | |||||
| 5 | 2 | 1 | 1 | |||
| 0 | 0 | 0 | 0 | 0 | ||
| 1 | 0 | 0 | 0 | 1 | ||
| 2 | 0 | 0 | 1 | 1 | ||
| 3 | 0 | 1 | 0 | 1 | ||
| 4 | 0 | 1 | 1 | 1 | ||
| 5 | 1 | 0 | 0 | 0 | ||
| 6 | 1 | 0 | 0 | 1 | ||
| 7 | 1 | 0 | 1 | 1 | ||
| 8 | 1 | 1 | 0 | 1 | ||
| 9 | 1 | 1 | 1 | 1 | ||
На рис. 2.68 показана обобщенная логическая система для двух разрядов одной декады двоично-десятичного счетчика.

Рис. 2.68. Обобщенная логическая схема для двух разрядов одной декады счетчика
Дешифраторы
Дешифратор (ДШ) - ФУ, который предназначен для декодирования (определения) состояния регистров или счетчиков, т.е. преобразования двоичного или иного кода в единичный позиционный код.
На рис. 2.69 показано объединение регистра и дешифратора в одну схему.

Рис. 2.69. Объединение регистра и дешифратора
Составим МОДИС-описание логической схемы дешифратора для трехразрядной двоичной переменной X.
X = {X0, X1...X3}
D0 ‘:=‘ IX0 * IX1 * IX2 * IX3;
D1 ‘:=‘ X0 * IX1 * IX2 * IX3;
...
D15 ‘:=‘ X0 * X1 * X2 * X3;
Дешифраторы бывают одноступенчатые (рис.2.70), двухступенчатые и многоступенчатые.
Рассмотрим одноступенчатый дешифратор.

Рис. 2.70. Принципиальная схема одноступенчатого дешифратора
|
|
|
Сложность логической схемы дешифратора оценивается по суммарному количеству входов всех логических элементов, входящих в его состав. Для одноступенчатого дешифратора
M = n  - количество входов ЛС.
- количество входов ЛС.
n –количество разрядов в двоичном коде.
Если n =10, то M = 10 ∙1024 = 104 для одноступенчатого ДШ.
Рассмотрим теперь двухступенчатый дешифратор.
Допустим, что на входе дешифратора функция шести переменных
 .
.
Запишем логическое выражение для одного из выходов дешифратора в виде конъюнкции от шести переменных X [0: 5]. Затем с помощью круглых скобок представим его в виде произведения двух конъюнкций от трех переменных. Таким же образом нужно записать выражения для всех остальных выходов дешифратора
 .
.
Первая конъюнкция в круглых скобка представляет собой один из выходов одноступенчатого дешифратора функции трех переменных X [0 :2], вторая конъюнкция - соответственно от переменных X [3 :5]. Произведение двух этих конъюнкций в круглых скобках представляет собой вторую ступень дешифратора.
Соответствующая логическая схема двухступенчатого дешифратора представлена в виде фрагмента на рис. 2.71. Подсчитаем суммарное количество входов логических схем для двухступенчатого дешифратора.


Рис. 2.71. Двухступенчатый дешифратор
На рис. 2.71 имеются два дешифратора первой ступени, каждый из них на три входных переменных, и один дешифратор второй ступени, который объединяет оба дешифратора первой ступени.
М2ст = ( n/2*2*n/2)*2+2*2n = n*2n/2 + 2n+1
При очень большом количестве разрядов строятся многоступенчатые дешифраторы.

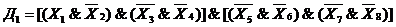 .
.
Качество дешифраторов характеризуется, кроме того, быстродействием.
 - задержка логического элемента “И”.
- задержка логического элемента “И”.
Временное запаздывание одноступенчатого дешифратора  , двухступенчатого -
, двухступенчатого -  .
.
При проектировании дешифратора необходимо выбрать некоторый оптимум между сложностью аппаратуры и временной задержкой, которую он вносит в систему.
Аналогично можно построить и двоично-десятичный дешифратор (рис.2.72).

Рис. 2.72. УГО двоично-десятичного дешифратора

Шифраторы
Шифратор – функциональный узел, обеспечивающий преобразование различных кодов из одной формы представления в другую. На рис. 2.73 изображено УГО шифратора.

Рис. 2.73 . УГО шифратора
Таблица 2.21
| Десятичная цифра | Двоично-десятичный код | |||
| Q4 | Q3 | Q2 | Q1 | |
| 4 | 2 | 2 | 1 | |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 1 | 0 |
| 5 | 1 | 0 | 0 | 1 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 0 | 1 | 1 |
| 8 | 1 | 1 | 1 | 0 |
| 9 | 1 | 1 | 1 | 1 |

Рис. 2.74. Схема подключения двоично-десятичного шифратора
Чаще всего используют шифраторы, обеспечивающие преобразование единичного позиционного кода в двоичный или двоично-десятичный. Шифраторы используют в устройствах ввода информации в ЭВМ, они обеспечивают перевод десятичного кода во внутренний код ЭВМ.
В табл. 2.21 представлена таблица соответствия единичного позиционного кода для десяти цифр и двоично-десятичного кода 4221.
Рассмотрим применительно к этой таблице пример построения шифратора. На рис. 2.74 изображена схема связи клавиатуры через шифратор с триггерами Q(1:4).
Пользуясь табл. 2.21, запишем МОДИС-описание схемы управления триггерами, например, для Q3.
Q3’:=’ ‘ЕСЛИ’ ( КН0 V КН1 V КН2 V КН3 V КН5 V КН6 V КН7) *ПР ‘ТО’ 0 ‘ИНЕСЛИ’( КН4 V КН8 V КН9 )* ПР ‘ТО’ 1‘ИНАЧЕ’ Q3;
Таким же образом составим описание схемы для остальных триггеров декады. Далее в соответствии с МОДИС-описанием строится логическая схема шифратора.
Мультиплексор
Мультиплексор - ФУ, обеспечивающий передачу данных с одного из нескольких входов на выход в зависимости от значения управляющего сигнала.

Рис. 2.75. УГО мультиплексора
На рис. 2.75 показано УГО, а на рис. 2.76 представлена логическая схема мультиплексора.
{X1÷ Xn } -информационные входы
{V1÷ Vk } - управляющие входы
F ’:=‘ ‘ЕСЛИ’ D1 ‘ТО’ X1
‘ИНЕСЛИ’ D2 ‘ТО’ X2
....
‘ИНЕСЛИ’ Dn ‘ТО’ Xn
‘ИНАЧЕ’ 0;

Рис. 2.76. Логическая схема мультиплексора
Демультиплексор
Демультиплексор – ФУ, который обеспечивает передачу входного сигнала на один из нескольких выходов в зависимости от значения управляющего сигнала. Логическая схема и УГО демультиплексора показаны на рис. 2.77 и рис. 2.78. На схемах обозначены
X÷ -информационный вход
{V1÷ Vk } - управляющие входы
{F1÷ Fn } – выходы
Мультиплексор и демультиплексор используются в составе различных цифровых устройств для преобразования параллельных кодов в последовательные и обратно.
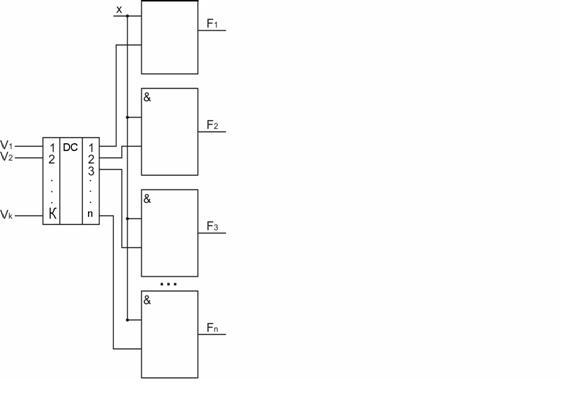
Рис. 2.77. Логическая схема демультиплексора

Рис. 2.78. УГО демультиплексора
Сумматоры
Сумматор – ФУ, который выполняет арифметическую операцию сложения. Сумматоры классифицируются по ряду признаков:
1) в зависимости от числа разрядов в слагаемых на:
а) одноразрядные,
б) многоразрядные;
2) в зависимости от системы счисления на:
а) двоичные,
б) двоично-десятичные;
3) по способу организации переноса между разрядами на сумматоры:
а) с последовательным переносом,
б) с параллельным переносом,
в) с групповым переносом;
4) по принципу действия на:
а) комбинационные, для построения которых используют только логические элементы,
б) накапливающие - основаны на использовании триггеров со счетным входом.
2.11.8.1. Полусумматор одноразрядный
Полусумматор одноразрядный – это логическая схема, обеспечивающая суммирование двух двоичных цифр.
В табл. 2.22 представлена таблица истинности полусумматора , и, в соответствии с этой таблицей, составлены логические функции для полусуммы (П) и переноса (q).
а, b – слагаемые; М2( a,b) - сумма по модулю 2; q – перенос ;

 П = а & b V a & b = а
П = а & b V a & b = а  b = М2( a,b);
b = М2( a,b); 
 q = а & b.
q = а & b.
Таблица 2.22
| а | b | П | q |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |

 Рис. 2.79. УГО сумматора по модулю 2
Рис. 2.79. УГО сумматора по модулю 2
УГО сумматора по модулю 2 изображено на рис.2.79 и УГО полусумматора - рис. 2.80. Как следует из табл. 2.22, если а = в,
то М2( a,b)=0, т.е. сумма четна. Если же а≠в, то М2( a,b)=1 , т.е. сумма нечетна.
Могут быть построены логические схемы полусумматоров комбинационного типа (рис. 2.81) и накапливающего типа (рис. 2.82).

Рис. 2.80. УГО полусумматора

Рис. 2.81. Логическая схема комбинационного полусумматора

Рис. 2.82. Логическая схема накапливающего сумматора
Накапливающий полусумматор строится на основе триггера со счетным входом. На рис. 2.82 триггер выполняет функцию полусуммирования.
Если на счетный вход подать в последовательном коде многоразрядную двоичную переменную
А = f (a1, a2, a13,… ak ),
то подсчитывается четность числа единиц в этой переменной.
2.11.8.2. Одноразрядный трехвходовой сумматор
Это ФУ, обеспечивающий суммирование трех одноразрядных двоичных цифр. Правила работы такого сумматора задаются с помощью табл. 2.23.
В этой таблице обозначено:
ai - i -тый разряд 1-го слагаемого,
bi - i -тый разряд 2-го слагаемого,
Si - i -тый разряд суммы,
Pi+1 - перенос в следующий разряд.
:
Таблица 2.23
| аi | вi | pi | Si | pi+1 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Пользуясь табл. 2.23, составим логические выражения для суммы в данном разряде и переноса в следующий разряд.









 Si = ai & bi & pi V ai & bi & pi V ai & bi & pi V ai & bi & pi V =
Si = ai & bi & pi V ai & bi & pi V ai & bi & pi V ai & bi & pi V =






 = pi & (ai & bi V ai & bi) V pi & (ai & bi V ai & bi) =
= pi & (ai & bi V ai & bi) V pi & (ai & bi V ai & bi) =


 = pi & М2 (ai,bi) V pi & М2 (ai,bi) = М2 { pi ,Пi }
= pi & М2 (ai,bi) V pi & М2 (ai,bi) = М2 { pi ,Пi }
pi+1 = ai & bi & pi V ai & bi & pi V ai & bi & pi V ai & bi & pi V =
= ai & М2 (bi , pi ) V pi & bi = ai & bi V pi &Пi.

Рис. 2.83. Схема одноразрядного трехвходового сумматора
Руководствуясь табл. 2.23, построим логическую схему одноразрядного трехвходового сумматора (рис. 2.83) и УГО (рис.2.84).

Рис. 2.84. УГО одноразрядного трехвходового сумматора
2.11.8.3. Многоразрядные сумматоры
Многоразрядные сумматоры предназначаются для нахождения арифметической суммы многоразрядных чисел.
А { а0, а1.....аn } + B { в0, в1.....вn } = S { S0, S1, ...Sn }.
Различают два основных типа:
1) последовательного действия,
2) параллельного действия.
Многоразрядный сумматор последовательного действия обеспечивает определение арифметической суммы чисел, поступающих на сумматор в последовательном коде.
Для правильной работы сумматора последовательного типа необходимо выполнять следующие требования:
если tp - время формирования переноса в одном разряде,
то tз ≥ tp -время задержки сигнала в цепи обратной связи переноса.
На рис. 2.85 показано УГО многоразрядного сумматора последовательного действия, а на рис.2.86 приведена его функциональная схема.

Рис. 2.85. УГО многоразрядного сумматора последовательного действия
tсдв- период следования импульсов СДВ tсдв ≥ tр .
Время получения суммы в схеме на рис. 2.86 будет
Τ∑посл ≈ nΤсдв

Рис. 2.86. Схема многоразрядного сумматора последовательного действия
Схема многоразрядного сумматора параллельного действия с последовательным переносом представлена на рис.2.87. УГО - на рис. 2.88.
Τ∑пар ≈ ntр -время сложения в многоразрядном сумматоре параллельного действия, а так как период следования импульсов сдвига много больше, чем время формирования переноса в одном разряде, то сумматор параллельного действия обладает в n - раз большим быстродействием, чем последовательный.

Рис. 2.87. Логическая схема многоразрядного сумматора параллельного действия с последовательным переносом
Многоразрядный сумматор параллельного действия с последовательным переносом содержит столько сумматоров, сколько разрядов в слагаемых.

Рис. 2.88. УГО многоразрядного сумматора параллельного действия
2.11.8.4. Многоразрядные сумматоры по модулю 2
Это ФУ, предназначенные для подсчета по модулю 2 количества единиц в многоразрядных кодах. Многоразрядные сумматоры по модулю 2 используются в системах контроля правильности передачи данных или преобразователях информации.
Существуют две основные схемы многоразрядных сумматоров по мод.2:
а) последовательная, б) пирамидальная.
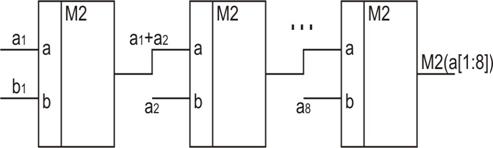
Рис. 2.89. Последовательный сумматор по модулю 2
На рис. 2.89 приведена логическая схема последовательного сумматора по мод. 2, на рис. 2.90 показано его УГО.
На рис. 2.91 – логическая схема для сумматора по мод. 2 пирамидального типа.

Рис 2.90. УГО сумматора по модулю 2

Рис. 2.91. Сумматор по мод. 2 пирамидального типа
Затраты оборудования на n входных переменных такие же, как для последовательной структуры. Быстродействие пирамидальной схемы выше, чем быстродействие последовательной схемы.
Контрольные вопросы
1. При каких дополнительных условиях триггеры JK и D переходят в режим Т-триггера?
2. Какие функциональные узлы преобразуют двоичный параллельный код в последовательный код?
3. Какие функциональные узлы преобразуют двоичный последовательный код в параллельный код?
4. Триггер какого типа является основой для построения двоичного счетчика?
5. Емкость двоичного счетчика N=1000. Какое количество триггеров необходимо для его построения, какой способ организации переноса наиболее предпочтительный?
6. Двоичный дешифратор имеет 128 выходов. Сколько должно быть входов на логической схеме дешифратора?
7. Демультиплексор имеет 5 управляющих входов. Назовите максимально возможное число выходов логической схемы демультиплексора?
8. Задан 8-разрядный двоичный код X [1÷8]=10110111. Вычислить 9-й контрольный разряд из условия контроля правильности передачи информации по-четности, построить соответствующую логическую схему формирования контрольного разряда.
9. Задан 8-разрядный двоичный код X [1÷8]=10110011. Вычислить 9-й контрольный разряд из условия контроля правильности передачи информации по-нечетности, построить соответствующую логическую схему формирования контрольного разряда.
10. Построить таблицу соответствия десятичного кода и двоично-десятичного кода 3321.
11. На вход шестиразрядного двоичного счетчика поступило 53 импульса. Какой код установится на счетчике?
12. Функционирование двухтактного триггера задано временной диаграммой. Назовите тип этого триггера.

13. Функционирование двухтактного триггера задано временной диаграммой. Назовите тип этого триггера.

14. Функционирование двухтактного триггера задано временной диаграммой. Назовите тип этого триггера.

Дата добавления: 2018-05-12; просмотров: 1363; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
