Принципы построения модели цифрового автомата (ЦА)
Модель ЦА состоит из трех частей:
1) описание переменных,
2) описание схемы (статическая часть модели),
3) описание временной диаграммы (динамическая часть модели).
Описание переменных
В зависимости от способа образования переменных в модели они делятся на две группы:
1) зависимые – “ЗАВИСИМ”;
2) независимые:
а) потенциальные независимые “ПНЕЗАВ”,
б) импульсные независимые “ИНЕЗАВ”.
Независимые переменные поступают на схему извне. Зависимые образуются внутри схемы и на ее выходах.
Описание схемы
При описании схем различают два типа цифровых автоматов:
1) синхронный,
2) асинхронный.
Синхронный ЦА отличается тем, что все изменения в модели происходят синхронно, в моменты начала тактов.
Асинхронный ЦА содержит в своем составе некоторые временные задержки, и изменения состояния модели происходят в произвольные моменты времени.
На рис. 2.48 показано УГО цифрового автомата.

Рис. 2.48. УГО ЦА
На этом рисунке:
x(t) – входной вектор,
s(t)- вектор состояния, 
y( t+1 ) - вектор выходного сигнала ЦА.
Уравнения синхронного ЦА:
y(t+1)=F {s(t), x(t)}
s(t+1)=  {s(t), x(t)}
{s(t), x(t)}
Уравнения для асинхронного ЦА отличаются тем, что его выходы и новые состояния определяются предысторией функционирования автомата за целый ряд тактов.
y(tn) = F1 { S( t-1), S(t-2),....S( t-n ), X( tn)}
S(tn) = φ1 { S( t-1), S(t-2),....S( t-n ), X( tn)}
Описание схемы для синхронного автомата выполняется по-разному, в зависимости от типа схемы.
Комбинационная схема отличается тем, что состоит только из комбинационных ЛЭ. Существуют два способа описания:
1) логическим выражением,
2) условным предложением.
На рис. 2.49 показана схема комбинационного автомата, ниже даны оба способа ее описания.

Рис. 2.49. Схема комбинационного автомата
1) F ’:=‘ (IА * B) V (IC * D * E);
2) F ’:=’ ЕСЛИ (IA * B) V (IC * D * E) то ‘1’, ‘ИНАЧЕ’ ‘0’;
Принцип описания схемы с запоминающими элементами состоит в том, что последовательно записываются условия, при выполнении которых изменяют свое состояние запоминающие элементы (ЗЭ) данной схемы. Описание логической схемы заканчивается символом “;”.

Рис. 2.50. УГО ЦА с запоминающими элементами
На рис. 2.50 показано УГО ЦА с запоминающими элементами , ниже приведен принцип описания такой схемы.
Вз ’: =‘ ‘ЕСЛИ’ А1 ‘ТО’ S1
’ИНЕСЛИ’ А 2 ‘ТО’ S2
‘ИНЕС ЛИ’ АК ‘ТО’ SK
‘ИНАЧЕ’ Вз;
Методику составления модели ЦА рассмотрим на примере логической схемы, представленной на рис. 2.51.
Описание переменных
‘ИНЕЗАВ’ Х2, Y0, ГШ,C4;
“ПНЕЗАВ” X1 , ВЫД.;
“ЗАВИСИМ” Q, F1 , F2.;
Описание схемы триггера
Q ‘: =‘ ‘ЕСЛИ’ (x1 * х2) ‘ТО’ 1
‘ИНЕСЛИ’ (y0 V ГШ) ‘ТО’ 0
‘ИНЕСЛИ’ C4 ‘ТО’ IQ
‘ИНАЧЕ’ Q;
Описание выходов схемы, представленной на рис. 2.51
F  ’:=‘ Q & ВЫД; F2’:=‘ IQ & ВЫД; .
’:=‘ Q & ВЫД; F2’:=‘ IQ & ВЫД; .
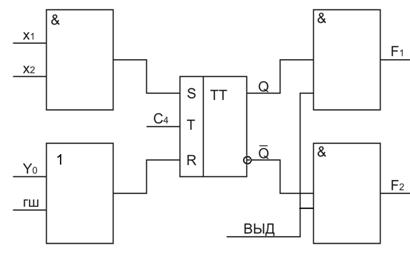
Рис. 2.51. Пример логической схемы
Временная диаграмма сигналов на входе триггера приведена на рис. 2.52.
В состав языка входит ряд операторов ввода и вывода данных, а также предусмотрены способы задания различных критериев моделирования, благодаря чему моделируемая система может обнаружить неисправности схемы в автоматическом режиме.
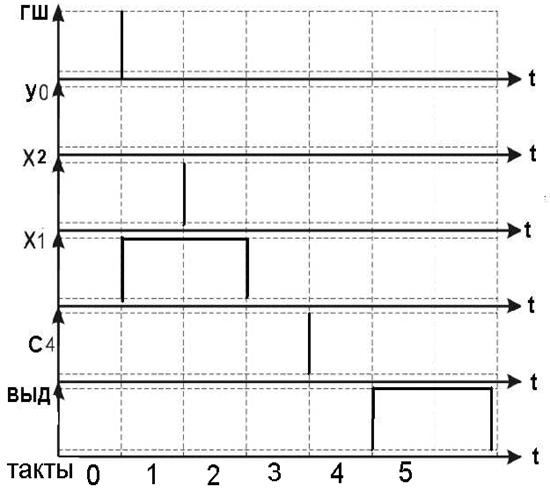
Рис.2.52. Фрагмент временной диаграммы
Описание фрагмента временной диаграммы дано ниже.
‘ВД’ ФРАГМЕНТ
‘НАЧАЛО’
‘ТАКТ’1: ГШ, X1;
‘ТАКТ’2: Х2;
‘ТАКТ’3: X1 = 0; 
‘ТАКТ’4: C4;
‘ТАКТ’5: ВЫД;
‘ТАКТ’7: ВЫД =0;
‘КОНЕЦ’
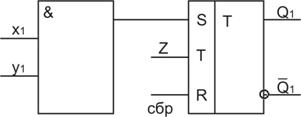
Рис. 2.53. Пример схемы
На рис. 2.53 показан пример схемы, состоящей из комбинационного элемента и триггера, ниже приведено описание схемы.
Q1 ‘:=’ ‘ЕСЛИ‘ [(X1 * Y1) + Z * СБР] > 1 ‘ТО’ 
‘ИНЕСЛИ’ X1 * Y1 ‘ТО’ 1
‘ИНЕСЛИ’ Z ‘ТО’ IQ1
‘ИНЕСЛИ’ CБР ‘ТО’ 0
‘ИНАЧЕ’ Q1;
Первое предложение в описании схемы содержит контроль условия, при котором не допускается на входе триггера совпадение в одном временном такте нескольких сигналов. Если это условие выполнено, то возникает неопределенность в состоянии триггера, обозначаемая знаком 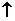 .
.
Дата добавления: 2018-05-12; просмотров: 414; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
