Розділ 2. Діелектрик в зовнішньому електричному полі
Лекція 1
Частина 1. Електростатика і магнетизм
Розділ 1. Електростатичне поле у вакуумі
Постійний електричний струм
1.1. Електростатика. Електричний заряд та його властивості
Електростатика – розділ електродинаміки, який вивчає взаємодію нерухомих електричних зарядів. Така взаємодія здійснюється через електростатичне поле.
Електричний заряд – це фізична величина, яка визначає інтенсивність електромагнітних взаємодій. Всі елементарні частинки характеризуються масою та електричним зарядом. Сила електромагнітних взаємодій набагато більша їх гравітаційної взаємодії. Значення сили електромагнітної взаємодії частинок визначається їх електричними зарядами.
Загалом в природі відомо чотири фундаментальні типи взаємодій:
- сильна;
- електромагнітна;
- слабка;
- гравітаційна.
Кожен вид взаємодії пов’язаний з певною характеристикою частинки. Так, гравітаційна залежить від маси частинки, а електромагнітна – від її електричного заряду.
Фундаментальні властивості електричного заряду:
1. Існує в двох видах – негативний (електрон) і позитивний (протон).
2. В будь-якій електрично-ізольованій системі алгебраїчна сума зарядів не змінюється . Ця властивість виражає закон збереження електричного заряду.
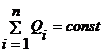 .
.
3. Електричний заряд є релятивістсько інваріантний (його величина не залежить від системи відліку, не залежить від того, рухається він чи знаходиться в стані спокою).
|
|
|
Для спрощення математичних розрахунків, прийнято вважати заряд не дискретним. Тоді його можна замінити піктивним безперервним розподілом. При переході до неперервного розподілу вводиться поняття густини заряду.
Виділяють лінійну (λ,τ), поверхневу (σ) та об’ємну (ρ) густину зарядів:
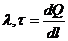 ;
;
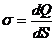 ;
;
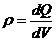 .
.
Закон збереження зарядів:
Електричні заряди не створюються і не зникають, а передаються від одного тіла до іншого або перерозподіляються всередині даного тіла.
Дробових зарядів в вільному стані не існує.
1.2. Закон Кулона
Основним законом електростатики є закон Кулона (1785 р.). Цей закон показує взаємодію двох нерухомих точкових зарядів або заряджених тіл, розміри яких малі порівняно з відстанями між ними.
Взаємодію заряджених тіл Кулон вивчав за допомогою крутильних вагів. Він виміряв силу взаємодії двох заряджених кульок в залежності від величини зарядів на них та від відстані між ними. При цьому Кулон виходив з того, що при дотику до зарядженої металічної кульки такої ж самої незарядженої кульки заряд розподіляється між обома кульками порівну.
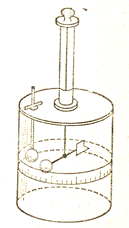 В результаті своїх дослідів Кулон прийшов до висновку, що: сила взаємодії двох нерухомих точкових зарядів пропорційна величині кожного з зарядів і обернено пропорційна квадрату відстані між ними.
В результаті своїх дослідів Кулон прийшов до висновку, що: сила взаємодії двох нерухомих точкових зарядів пропорційна величині кожного з зарядів і обернено пропорційна квадрату відстані між ними.
|
|
|
Напрямок сили співпадає з прямою, що сполучає заряди. В умовах цієї взаємодії однойменні заряди відштовхуються, а різнойменні притягуються (рис.1.1).
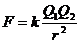 ,
,
k – коефіцієнт пропорційності (залежить від вибору системи одиниць)
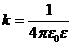 ,
,
Рис.1.1
де ε – діелектрична проникливість середовища, ε0 – електростатична стала (ε0=8,85·10-12 Ф/м).
В системі СІ одиниця електричного заряду – Кл („кулон”).
1 Кл – електричний заряд, який проходить за 1с через поперечний переріз провідника при струмі 1А.
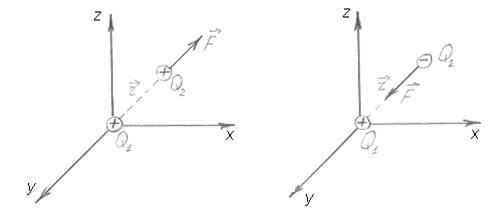
Рис.1.2
Таким чином, електростатичне поле – особливий вид матерії, пов’язаний з електричними зарядами і яка передає дії зарядів з одного на другий. Електричне поле не виникає при взаємодії зарядів. Будь-який заряд завжди має електричне поле. Якщо заряд нерухомий, то поле називається електростатичним. Воно не змінюється в часі і створюється лише електричними зарядами.
Електричне поле має специфічні фізичні властивості. На електричні заряди цього поля діють сили, пропорційні цим зарядам. Якщо потрібно виявити електричне поле, то в місце знаходження заряду вносять інший заряд. Для визначення властивостей поля використовують пробний одиничний позитивний заряд Qпр, нехтуючи його власним полем. На Qпр діє сила
|
|
|

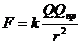 .
.
1.3. Напруженість електричного поля
Якщо в ту саму точку поля вносити різні заряди, то на них будуть діяти різні сили, але відношення сил до величини заряду буде зберігатися сталим для цієї точки поля:
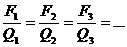
Для різних точок поля можна скласти аналогічні співвідношення.
Відношення сили до величини пробного заряду називається напруженістю електричного поля. Напруженість – силова характеристики електричного поля; відношення сили до величини пробного заряду.
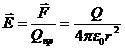 ,
,
r – відстань від заряду Q, який створює поле до точки поля, де визначається напруженість.
Напруженість показує яка сила діяла б на одиничний позитивний (пробний) заряд, вміщений в дану точку поля. Е – векторна величина; за напрям беруть напрям сили, з якою заряд Q діє на дану точку.
Лінії, дотичні до яких в кожній точці збігаються з вектором напруженості в даній точці поля називаються лініями напруженості, або силовими лініями. Силові лінії ніколи не можуть бути замкнені самі на себе – вони завжди мають початок і кінець або йдуть у нескінченність. Вони направлені від позитивного заряду до негативного (виходять з позитивного заряду і входять в негативний). Лінії напруженості ніколи не перетинаються.
|
|
|
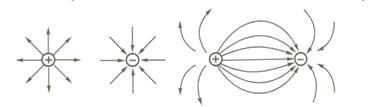
Рис.1.3
Електричне поле, у всіх точках якого напруженість однакова за величиною і напрямком називається однорідним (тобто заряд рівномірно розподілений по площині). Прикладом однорідного поля може бути поле плоского конденсатора на деякій відстані від країв пластин конденсатора.
Принцип суперпозиції полів(накладання електричних полів).
Результуюча сила, що діє на заряд Q з боку інших зарядів Q1 >0 і Q2<0 буде дорівнювати геометричній сумі сил F1 і F2 з боку зарядів Q1 і Q2.
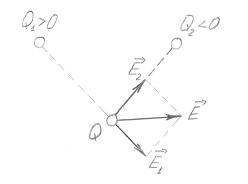
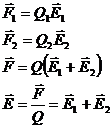
Якщо поле створене двома зарядами, напруженість визначається за теоремою косинусів:
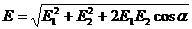 .
.
Рис.1.4
В загальному випадку: якщо в певній точці поля різні заряджені частинки створюють поля з напруженостями Е1, Е2, Е3... Еn , то результуюча напруженість поля в точці:

1.4. Потенціал електричного поля
Потенціал – енергетична характеристика електричного поля, що показує яку роботу треба затратити, щоб перемістити заряд в дану точку поля, або перенести його з даної точки поля у нескінченність. Потенціал характеризує потенціальну енергію яку мав би позитивний одиничний заряд, вміщений в дану точку поля.
Робота по переміщенню не залежить від форми шляху, а залежить лише від розміщення початкової і кінцевої точок траєкторії. Робота по переміщенню заряду, яка виконується в електричному колі по замкненому контуру дорівнює нулю.
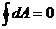 .
.
При переміщенні зарядів змінюється їх взаємне розміщення і тому робота електричних сил дорівнює зміні потенціальної енергії заряду, що переміщується.
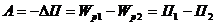 .
.
Потенціальна енергія заряду в електричному полі визначається за формулою:
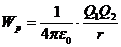 .
.
Таким чином, потенціал φ
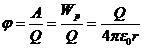 .
.
Формула справедлива, якщо φ→0 при r→0.
1.5. Зв’язок між напруженістю і потенціалом
Напруженість і потенціал є різними характеристиками однієї точки поля.
Розглянемо роботу електричних сил в електричному полі при переміщенні електричного заряду з точки 1 в точку 2.
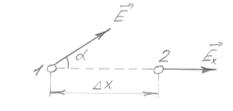 A= QEx∆x;
A= QEx∆x;
A=Q (φ1 –φ2)= - Q∆φ.
Прирівнявши обидва вирази для роботи, дістанемо:
QEx∆x=- Q∆φ,
Рис.1.5
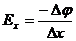 .
.
Аналогічно, 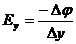 ,
,
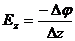 .
.
Таким чином, Е= - gradφ.
Напруженість в будь-якій точці поля дорівнює швидкості зміни потенціалу в цій точці поля, взятій з протилежним знаком. Знак „мінус” показує, що вектор напруженості направлений в бік спадання потенціалу, тобто вектори напруженості і потенціалу протилежно направлені.
1.6. Еквіпотенціальні поверхні
Уявна поверхня, всі точки якої мають однаковий потенціал називаються еквіпотенціальними поверхнями. Їх рівняння мають вигляд:
φ(x, y ,z)=const.
При переміщенні по еквіпотенціальній поверхні на dl потенціал φ не змінюється (dφ=0). Тоді дотична до поверхні складова вектора напруженості дорівнює нулю. Отже, вектор напруженості в кожній точці направлений по нормалі до еквіпотенціальної поверхні, яка проходить через дану точку. Звідси, лінії напруженості в кожній точці ортогональні до еквіпотенціальної поверхні.
Еквіпотенціальну поверхню можна провести через будь-яку точку поля, тоді таких поверхонь може бути безліч. Проводять такі поверхні таким чином, щоб різниця потенціалів для двох сусідніх поверхонь була всюди одна і та ж сама. В такому випадку, по густині еквіпотенціальних поверхонь можна судити про величину напруженості поля. Чим густіше розташовані еквіпотенціальні поверхні, тим швидше змінюється потенціал при переміщенні вздовж нормалі до поверхні, відповідно, тим більше в даному місці 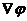 і Е.
і Е.
 Для однорідного поля еквіпотенціальні поверхні представляють собою систему рівновіддалених одна від одної площин, перпендикулярних до напрямку поля.
Для однорідного поля еквіпотенціальні поверхні представляють собою систему рівновіддалених одна від одної площин, перпендикулярних до напрямку поля.
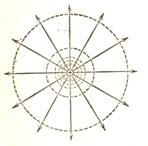
Для точкового заряду еквіпотенціальні поверхні можна представити у вигляді, показаному на рис.1.5.
Рис.1.6
1.7. Електричний диполь
Електричним диполем називається система двох однакових за величиною різнойменних точкових зарядів +q і –q, відстань l між якими значно менша відстані до тих точок, в яких визначається поле системи. Пряма, яка проходить через обидва заряди називається віссю диполя; l – плече диполя.
Поле диполя має осьову симетрію. Якщо відстань між зарядами не змінюється, то такий диполь називається жорстким. Якщо довжина плеча диполя l мала порівняно з відстанню r до точки спостереження, то такий диполь називається точковим.
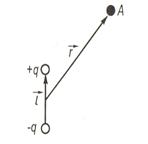 Основною характеристикою електричного диполя є його електричний дипольний момент р – вектор, який чисельно дорівнює добуткові заряду на плече і направлений від негативного заряду до позитивного.
Основною характеристикою електричного диполя є його електричний дипольний момент р – вектор, який чисельно дорівнює добуткові заряду на плече і направлений від негативного заряду до позитивного.
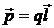 .
.
Рис.1.7
1.8. Електричний диполь в однорідному зовнішньому електричному полі
Розглянемо дію зовнішнього електричного поля на диполь.
Якщо поле однорідне, то сили, які діють на негативний і позитивний заряди диполя є однаковими за значенням і протилежними за напрямом, тобто утворюють пару сил(рис1.8). Відповідно їх рівнодія дорівнює нулю.
Дія пари сил характеризується моментом пари:
M= qElsinα,
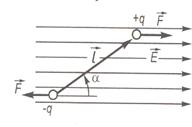 α – кут між вектором l і напруженістю поля Е.
α – кут між вектором l і напруженістю поля Е.
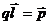 , тоді
, тоді
М=plsinα.
Або у векторній формі
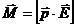 .
.
Рис.1.8
Отже, в однорідному електричному полі на диполь діє пара сил, яка намагається повернути диполь так, щоб кут між векторами р і Е зменшився і диполь встановився в напрямку поля.
Існують два положення рівноваги диполя:
- диполь паралельний електричному полю (стійка рівновага);
- диполь антипаралельний йому (нестійка рівновага).
Енергія диполя в однорідному електричному полі напруженістю Е:
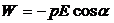 .
.
1.8. Електричний диполь в неоднорідному зовнішньому електричному полі
Якщо поле неоднорідне, то сили F1 і F2 за значенням є різними і їхня рівнодія не дорівнює нулю.
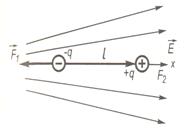 Знайдемо рівнодійну силу. Вважатимемо, що диполь розміщений вздовж однієї з силових ліній (рис 1.9). Тоді
Знайдемо рівнодійну силу. Вважатимемо, що диполь розміщений вздовж однієї з силових ліній (рис 1.9). Тоді 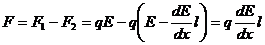 .
.
Таким чином, в неоднорідному електричному полі на диполь крім моменту пари сил, діє ще сила в напрямі зростання напруженості поля, яка прагне втягнути диполь в область сильнішого поля.
Рис. 1.9
Лекція 2
Опис векторного поля
2.1. Потік вектора напруженості
Нехай рух рідини характеризується полем вектора швидкості. Об’єм рідини, який протікає за одиницю часу через деякий переріз S, називається потоком рідини через цю поверхню. Щоб знайти потік потрібно розбити поверхню на елементарні ділянки ∆S.
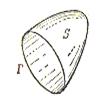 Розглянемо поле вектора напруженості. Будемо вважати, що густота ліній напруженості буде дорівнювати по модулю самому вектору напруженості і тоді число ліній, які будуть пронизувати елементарну площину dS буде знаходитися, як добуток EdScosα (нормаль n до поверхні буде складати кут α з вектором Е). Це і є потік dФ вектора Е через площину dS.
Розглянемо поле вектора напруженості. Будемо вважати, що густота ліній напруженості буде дорівнювати по модулю самому вектору напруженості і тоді число ліній, які будуть пронизувати елементарну площину dS буде знаходитися, як добуток EdScosα (нормаль n до поверхні буде складати кут α з вектором Е). Це і є потік dФ вектора Е через площину dS.
Рис.2.1
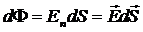 , (2.1)
, (2.1)
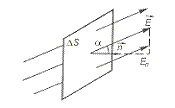 Еn – проекція Е на нормаль n, dS – вектор, модуль якого чисельно дорівнює dS, а напрям співпадає з напрямом нормалі до площини. Нормаль може бути направлена в обидва боки.
Еn – проекція Е на нормаль n, dS – вектор, модуль якого чисельно дорівнює dS, а напрям співпадає з напрямом нормалі до площини. Нормаль може бути направлена в обидва боки.
Якщо є поверхня довільної форми, то потік визначається інтегруванням
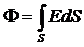 . (2.2)
. (2.2)
Рис. 2.2
Потік вектора Е – алгебраїчна величина, залежить від вибору напряму нормалі n і конфігурації поля вектора напруженості.
2.2. Теорема Гауса
Запишемо теорему Гауса, яка в деяких випадках спрощує знаходження напруженості електричного поля: потік вектора напруженості через замкнену поверхню дорівнює алгебраїчній сумі зарядів, які містяться всередині цієї поверхні, поділеній на ε0:
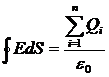 . (2.3)
. (2.3)
Доведення:
Розглянемо поле одного заряду Q. Нехай, даний заряд знаходиться в деякій замкненій поверхні S (рис.2.3).
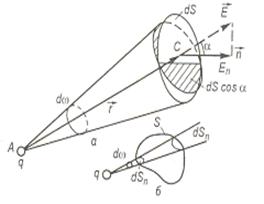 Розглянемо потік вектора напруженості через деякий елемент dS.
Розглянемо потік вектора напруженості через деякий елемент dS.
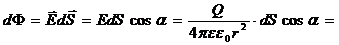
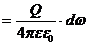 (dω =4π).
(dω =4π).
Величина 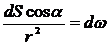 , dω – кут, який опирається на дану поверхню з вершиною в точці, де знаходиться заряд Q.
, dω – кут, який опирається на дану поверхню з вершиною в точці, де знаходиться заряд Q.
Рис.2.3
Інтегрування по площі S тотожне інтегруванню по всьому куту ω. Проінтегрувавши, отримаємо:
 .
.
Коли електричне поле створене системою зарядів Q1, Q2, Q3,... за принципом суперпозиції полів маємо:

Тоді потік вектора напруженості:
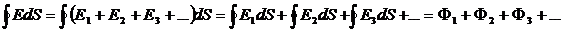
Якщо заряд знаходиться в замкненій поверхні, то він чисельно дорівнює 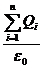 і він дорівнює нулю, якщо знаходиться ззовні поверхні.
і він дорівнює нулю, якщо знаходиться ззовні поверхні.
Нехай заряд рівномірно розподілено по об’єму V. Кожен елементарний об’єм dV утримує точковий заряд, що дорівнює ρdV і тоді в правій частині формули (3) матимемо:
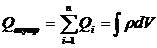 . (2.4)
. (2.4)
Інтегрування (2.4) ведемо лише по об’єму, який знаходиться всередині замкненої поверхні.
В той час, коли саме поле вектора напруженості залежить від конфігурації всіх зарядів, потік Е крізь деяку замкнену поверхню S визначається лише алгебраїчною сумою зарядів всередині S, а це означає, що якщо перемістити заряди, то поле напруженістю Е зміниться усюди і зміниться потік вектора Е через дану площу S. Але, якщо переміщення заряду відбулося без перетину поверхні S, то потік через дану поверхню залишиться незмінним, хоча саме поле напруженості може змінитися і досить суттєво.
2.3. Дивергенція вектора напруженості
Для визначення дивергенції вектора напруженості потрібно знайти диференціальну форму теореми Гауса і знайти зв’язок між об’ємною густиною заряду і зарядом, розподіленим в цьому об’ємі.
Представимо заряд в деякому об’ємі V, що охоплений замкненою поверхнею S. Внутрішній заряд Q визначається за формулою:
Qвнутр=<ρ>V,
де <ρ> − середнє по об’єму значення об’ємної густини заряду.
Підставимо цей вираз в рівняння теореми Гауса (2.3):
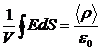 . (2.5)
. (2.5)
Спрямуємо даний об’єм до нуля, стягуючи його до точки поля, яка нас цікавить. Очевидно, що при цьому <ρ> буде прямувати до значення ρ в даній точці. Отже, відношення в лівій частині (2.5) буде прямувати до 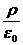 .
.
Величину, яка є границею відношення 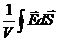 називають дивергенцією поля напруженості Е.
називають дивергенцією поля напруженості Е.
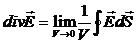 . (2.6)
. (2.6)
Аналогічно визначається дивергенція будь-якого іншого векторного поля. З (2.4) слідує, що дивергенція вектора Е є скалярною функцією координат. Щоб отримати divE потрібно проінтегрувати (2.6). Отриманий вираз буде залежати від вибору системи координат. Наприклад, в Декартовій системі координат:
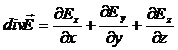 . (2.7)
. (2.7)
В диференціальній формі теорема Гауса записується у вигляді:
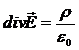 , або
, або 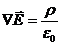
(при V→0 в рівнянні (5) права частина прямує до ρ/ε0, ліва частина прямує до divE).
В диференціальній формі теорема Гауса є локальною формою, divE залежить лише від ρ в тій самій точці і більше ні від чого.
В тих точках поля, де дивергенція вектора Е позитивна маємо справу з джерелами поля (там знаходяться позитивні заряди), а де вона негативна будуть стоки (негативні заряди). Таким чином, лінії напруженості починаються з джерел поля і закінчуються в місцях стоків.
2.4. Теорема Остроградського-Гауса
Знаючи дивергенцію вектора напруженості в будь-якій точці простору можемо знайти потік вектора Е через будь-яку замкнену поверхню кінцевих розмірів.
Розглянемо потік вектора швидкості для ідеальної рідини.
Добуток divV на dV дає потужність джерел рідини, які охоплені об’ємом dV, сума таких добутків дає сумарну алгебраїчну потужність джерел в усьому об’ємі V, по якому здійснюється інтегрування: 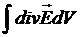 .
.
Внаслідок того, що рідина не стискається, сумарна потужність джерел поверхні дорівнює потоку рідини, що витікає назовні через поверхню S, яка обмежує об’єм V.
Таким чином,
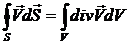 .
.
Цей вираз є математичним записом теореми Остроградського-Гауса.
Дана теорема справедлива для векторного поля будь-якої природи. І тому можемо записати:
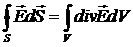 . (2.8)
. (2.8)
2.5. Циркуляція і ротор вектора напруженості
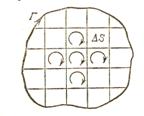
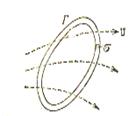 Уявимо замкнутий контур Г, через який рухається ідеальна рідина (рис.2.4). Заморозимо миттєво рідину у всьому об’ємі за виключенням тонкого замкненого каналу постійного перерізу, який включає контур Г. В залежності від характеру поля вектора швидкості, рідина в каналі буде або нерухомою, або буде циркулювати вздовж даного контуру.
Уявимо замкнутий контур Г, через який рухається ідеальна рідина (рис.2.4). Заморозимо миттєво рідину у всьому об’ємі за виключенням тонкого замкненого каналу постійного перерізу, який включає контур Г. В залежності від характеру поля вектора швидкості, рідина в каналі буде або нерухомою, або буде циркулювати вздовж даного контуру.
Рис. 2.4
В якості міри цього руху візьмемо величину 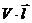 – добуток швидкості на довжину контуру – циркуляція вектора швидкості по контуру Г.
– добуток швидкості на довжину контуру – циркуляція вектора швидкості по контуру Г.
циркуляція V по Г=Vl.
Оскільки канал має постійний переріз, то 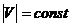 , в той момент, коли відбулося затвердіння стінок, у кожної з частинок рідини в каналі буде погашена складова швидкості, перпендикулярна до стінки і залишиться лише складова швидкості, дотична до контуру – Vl (тангенціальна складова). З даною складовою пов’язаний елементарний імпульс dpi, модуль якого для частинки рідини, яка знаходиться на відрізку каналу dl, має величину
, в той момент, коли відбулося затвердіння стінок, у кожної з частинок рідини в каналі буде погашена складова швидкості, перпендикулярна до стінки і залишиться лише складова швидкості, дотична до контуру – Vl (тангенціальна складова). З даною складовою пов’язаний елементарний імпульс dpi, модуль якого для частинки рідини, яка знаходиться на відрізку каналу dl, має величину 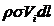 , де ρ – густина рідини, σ – площа поперечного перерізу каналу.
, де ρ – густина рідини, σ – площа поперечного перерізу каналу.
Так як рідина ідеальна, дія стінок може змінюватись лише вздовж dpi, але не впливає на його величину. При цьому алгебраїчна сума імпульсів не може змінитися, тобто імпульс, набутий однією з частинок чисельно дорівнює імпульсу, який втрачений іншою частинкою, тобто:
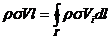 ,
,
де V – швидкість циркуляції, Vi – дотична складова швидкості рідини в об’ємі 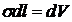 в момент часу перед затвердінням стінок каналу. Скоротивши на ρ і σ отримаємо:
в момент часу перед затвердінням стінок каналу. Скоротивши на ρ і σ отримаємо:
циркуляція 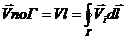 .
.
Аналогічно визначається циркуляція будь-якого вектора по довільному замкненому контуру. Тоді:
циркуляція 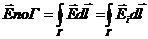 .
.
Якщо розглядати ламінарний рух рідини в річці, то швидкість біля дна дорівнює нулю і поступово збільшується при наближенні до поверхні води і лінії вектора швидкості будуть прямолінійними. Разом з тим, в полі з вигнутими лініями циркуляція може дорівнювати нулю.
Циркуляція вектора характеризує властивості поля, які мають середні значення по поверхні. Щоб отримати середні значення в точці Р, потрібно зменшити розміри контуру Г, відповідно зменшиться циркуляція і площа контуру.
Відношення циркуляції вектора до площі S прямує до деякої границі, яка використовується для характеристики поля в точці Р.
Візьмемо контур Г, який лежить в площині, яка проходить через точку Р і розглянемо вираз:
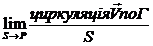 , (2.10)
, (2.10)
де S – площа, охоплена контуром Г. Для довільної площини дана границя не дає можливості визначити характеристику поля в точці Р, тому що залежить не лише від точки Р, а й від орієнтації контуру в просторі. Ця орієнтація може бути задана напрямом позитивної нормалі n до площі контуру Г. Позитивною вважають нормаль, яка зв’язана з напрямом обходу по контуру при інтегруванні правилом правого гвинта.
Визначаючи (2.10) в одній точці Р для різних напрямів нормалі отримаємо різні значення, причому для протилежних напрямів n вони відрізняються лише знаком. Для якогось напряму n величина (2.10) в даній точці буде максимальною. Таким чином, відношення (2.10) веде себе як проекція вектора на напрям n. Максимальне значення (2.10) визначає модуль даного вектора, а напрям позитивної нормалі, при якій досягається максимум дає напрям вектора. Даний вектор називається ротором, або вихром вектора V і позначається:
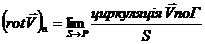 . (2.11)
. (2.11)
 Під
Під 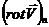 розуміється проекція вектора
розуміється проекція вектора 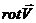 на позитивну нормаль до площини S, охопленої контуром Г.
на позитивну нормаль до площини S, охопленої контуром Г.
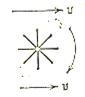
В тих місцях, де ротор відмінний від нуля, млинок рухається з тим більшою швидкістю, чим більша проекція ротора на вісь даного млинка.
Рис.2.5
2.6. Теорема Стокса
Знаючи ротор вектора швидкості в кожній точці поверхні S, можна знайти циркуляцію цього вектора по контуру Г.
Розіб’ємо поверхню на елементи dS.
За рівнянням (2.11) циркуляція швидкості по контуру, що обмежена поверхнею dS може бут представлена у вигляді:
циркуляція 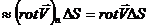 ,
,
де n – позитивна нормаль до елементу поверхні dS.
Просумуємо вирази по всій поверхні S і здійснимо граничний перехід, при якому всі значення ∆S →0. Отримаємо:
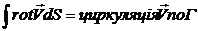 .
.
Дійсно, просумувавши всі 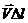 , побачимо, що вони взаємознищуються.
, побачимо, що вони взаємознищуються.
Для ділянки ∆S, яка лежить зліва MN, ділянка при визначенні циркуляції проходить в напрямі від N до M, а для ∆S справа від NM та сама ділянка проходить в напрямі від M до N і таким чином 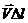 для суміжних площадок відрізняються лише знаком. Некомпенсованими будуть лише ті
для суміжних площадок відрізняються лише знаком. Некомпенсованими будуть лише ті 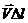 , які лежать ззовні контуру Г.
, які лежать ззовні контуру Г.
 Маємо:
Маємо:
 .
.
Теорема Стокса для вектора напруженості:
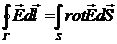 . (2.12)
. (2.12)
Рис. 2.6
Лекція 3
Обчислення напруженості поля
На підставі теореми Гауса
3.1. Неможливість стійкої рівноваги заряду в електричному полі
Нехай в вакуумі є система нерухомих точкових зарядів, які знаходяться в положенні рівноваги. Розглянемо один заряд Q, який знаходиться в замкненій поверхні S. Припустимо, що Q>0, тоді щоб рівновага була стійкою, необхідно, щоб у всіх точках S поле Е, яке утворене всіма іншими зарядами системи було направлене до Q. Лише в цьому випадку при будь-якому малому зміщенні Q з положення рівноваги на нього буде діяти повертаюча сила і положення рівноваги буде стійким. Але така конфігурація поля Е навколо Q протирічить теоремі Гауса. Потік Е крізь S буде негативним, а за теоремою Гауса він повинен дорівнювати нулю, бо цей потік створено зарядами, які розташовані зовні S. А те, що потік вектора напруженості чисельно дорівнює нулю означає, що в якихось точках поверхні S вектор Е направлений всередину, а в інших – назовні. Звідси висновок, що стійкої рівноваги заряду в будь-якому електростатичному полі не існує.
3.2. Поле рівномірно зарядженої площини
Нехай, заряд рівномірно розподілений по площині з поверхневою густиною σ. З міркувань симетрії очевидно, що вектор напруженості може бути тільки перпендикулярним до даної зарядженої площини і в симетричних відносно цієї площини точках, вектор Е однаковий за модулем і протилежний за напрямком.
Така конфігурація поля підказує, що в якості замкнутої поверхні для дослідження поля потрібно вибрати циліндр.
Вважаємо, що дана поверхнева густина додатна: σ>0.
Потік крізь кругову поверхню дорівнює нулю: Фб=0
Тому повний потік через всю поверхню циліндра:
Фn=2E∆S,
 де ∆S – площина кожного торця циліндра.
де ∆S – площина кожного торця циліндра.
Ззовні циліндра знаходиться певний заряд Q=σ∆S. За теоремою Гауса Фn=Q.
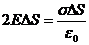 ,
,
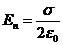 , (3.1)
, (3.1)
Рис.3.1
En – проекція вектора Е на нормаль n до зарядженої поверхні, причому вектор нормалі направлений до даної поверхні.
Відповідно до (3.1), коли σ >0 і напруженість електричного поля Еn>0. Це означає, що вектор Е направлений від зарядженої площини.
 Якщо σ<0, то Еn<0 (вектор Е направлений до зарядженої площини).
Якщо σ<0, то Еn<0 (вектор Е направлений до зарядженої площини).
Той факт, що Е не залежить від відстані до площини означає, що відповідне електричне поле є однорідним, тобто однакове зліва і справа від даної площини.
Отриманий результат справедливий лише для нескінченної однорідної плоскої поверхні (лише в цьому випадку справедлива симетрія), але також приблизно справедливий і для прилягаючої до поверхні частини.
Рис.3.2
3.3. Поле двох паралельних заряджених площин
Нехай кожна з площин має однакову за модулем але різну за знаком поверхневу густину заряду σ.
Поле двох заряджених площин можна знайти як суперпозицію полів, створюваних кожною площиною окремо. Між площинами напруженості полів додаються і мають однаковий напрям, тобто
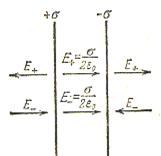
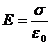 . (3.2)
. (3.2)
В даній формулі σ – модуль поверхневої густини заряду.
Рис. 3.3
Поле в даному випадку знаходиться між площинами і є однорідним в даній області. Результат справедливий і для площини кінцевих розмірів, якщо відстань між площинами набагато менша площі самих площин (плоский конденсатор).
Найбільш помітні відхилення однорідності лише поблизу пластин, але при розрахунках ними нехтують.
3.4. Поле нескінченного круглого циліндру
Нехай, поле створене нескінченною циліндричною поверхнею радіусом R і ця поверхня заряджена з постійною поверхневою густиною σ. З міркувань симетрії слідує, що напруженість поля в будь-якій точці направлена вздовж прямої, перпендикулярної осі циліндра. Величина напруженості не залежить від відстані r від осі циліндра.
Уявимо деяку коаксіальну замкнуту циліндричну поверхню радіуса r і довжини h.
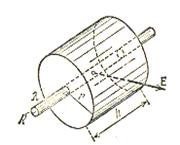 Для основи циліндра En=0. Напруженість електричного поля в даному випадку перпендикулярна до поверхні циліндра.
Для основи циліндра En=0. Напруженість електричного поля в даному випадку перпендикулярна до поверхні циліндра.
Для бічної поверхні циліндра En=E(r).
Вважатимемо, що заряд позитивний.
З даного слідує, що потік Е через бічну поверхню чисельно дорівнює 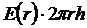 .
.
Рис.3.4
Якщо даний радіус r>R, всередину даної поверхні попаде весь заряд Q, який буде чисельно дорівнювати добутку лінійної густини даного заряду на довжину циліндра h.
Q=τh,
(τ – лінійна густина заряду).
Використаємо теорему Гауса:
 ;
;
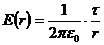 . (3.3)
. (3.3)
Формула (3.3) справедлива при r ≥R.
Якщо r<R, то замкнута поверхня не має всередині зарядів, внаслідок чого Е(r)=0.
Таким чином, всередині рівномірно зарядженої циліндричної поверхні нескінченної довжини поле відсутнє. Напруженість ззовні поверхні визначається лінійною густиною τ і відстанню r від осі циліндра.
Поле негативно зарядженого циліндра відрізняється від поля позитивно зарядженого циліндра лише напрямом вектора напруженості, але не його величиною.
З формули (3.3) слідує, що зменшуючи радіус циліндра R при незмінній лінійній густині заряду можна отримати поблизу поверхні циліндра поле з дуже великою напруженістю. Підставивши (3.3) в умову, що  і уявивши, що r=R, отримаємо для напруженості поля безпосередньо біля поверхні циліндра
і уявивши, що r=R, отримаємо для напруженості поля безпосередньо біля поверхні циліндра
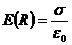 . (3.4)
. (3.4)
За допомогою принципу суперпозиції можна знайти поле двох коаксіальних циліндричних поверхонь з однаковою по величині але різною за знаком лінійною густиною τ. Тоді поле знаходиться між поверхнями.
 Всередині меншого і ззовні більшого циліндрів поле відсутнє, а між циліндрами величина напруженості визначається за допомогою формули (3.3).
Всередині меншого і ззовні більшого циліндрів поле відсутнє, а між циліндрами величина напруженості визначається за допомогою формули (3.3).
Це справедливо також для циліндричних поверхонь скінченої довжини, якщо відстань між поверхнями набагато менша їх довжини (циліндричний конденсатор). Відхилення помітні лише поблизу країв циліндра.
Рис. 3.5
3.5. Поле сферично зарядженої поверхні
Поле, створене сферичною поверхнею радіуса R, яка заряджена з поверхневою густиною σ буде центральносиметричним. Тобто напрям вектора напруженості в будь-якій точці, що проходить через центр сфери є функцією відстані R від центра сфери.
Уявимо концентричну поверхню радіуса r.
Для всіх точок цієї поверхні En=E(r).
Якщо r>R – всередину даної поверхні попаде весь заряд Q, розподілений по поверхні сфери і тому можна записати теорему Гауса:
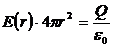 .
.
З даного рівняння
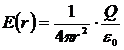 , (r ≥R). (3.5)
, (r ≥R). (3.5)
Сферична поверхня радіуса r меншого ніж R не буде мати зарядів, внаслідок чого для випадку r<R
Еn(r)=0.
 Таким чином всередині сферичної поверхні з постійною поверхневою густиною поле відсутнє, ззовні даної поверхні поле тотожне з полем точкового заряду тієї ж величини, розміщеного в центрі сфери.
Таким чином всередині сферичної поверхні з постійною поверхневою густиною поле відсутнє, ззовні даної поверхні поле тотожне з полем точкового заряду тієї ж величини, розміщеного в центрі сфери.
Використовуючи принцип накладання полів можна показати, що поле двох сферичних поверхонь, які несуть однакові заряди, але з протилежними знаками, буде знаходитись в проміжку між поверхнями, причому величина напруженості буде визначатися за формулою Е.
Рис.3.6
3.6. Поле об’ємно зарядженої кулі
Нехай куля радіусом R заряджена з постійною об’ємною густиною заряду ρ. Поле в даному випадку володіє центральною симетрією.
Для поля зовні кулі маємо той самий результат, що і для сферичної поверхні – рівняння (3.5). Але для точок всередині кулі результат інший.
Сферична поверхня (r<R) заключає в собі заряд
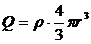 .
.
Тому теорема Гауса для такої поверхні набуде вигляду:
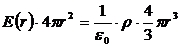 .
.
Об’ємна густина заряду 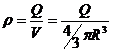 . Підставимо це значення в попередню формулу. Тоді
. Підставимо це значення в попередню формулу. Тоді

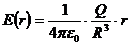 , (r≤R).
, (r≤R).
Таким чином, всередині кулі напруженість зростає лінійно з відстанню r до центра, а зовні кулі – спадає із збільшенням відстані r.

Рис. 3.7
Лекція 4
Розділ 2. Діелектрик в зовнішньому електричному полі
Діелектрик в зовнішньому
Електричному полі
4.1. Полярні і неполярні молекули
Всі речовини поділяються на провідники, діелектрики (ізолятори) і напівпровідники.
В природі ідеальних діелектриків не існує. Всі речовини в якійсь мірі проводять електричний струм, але діелектрики проводять струм в 1015—1020 раз гірше, ніж провідники.
Якщо діелектрик внести в електричне поле, то це поле і діелектрик набувають істотних змін. Щоб це зрозуміти потрібно врахувати, що в складі атомів і молекул є позитивно заряджені ядра і негативно заряджені електрони. Будь-яка молекула представляє собою систему, в якій сумарний заряд дорівнює нулю. Розміри даної системи малі – порядку декількох ангстрем (10-10 м). Поле, створене подібними системами, характеризується величиною дипольного моменту.
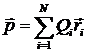 . (4.1)
. (4.1)
Сумування відбувається як по електронам, так і по ядрам. Щоправда, електрони в молекулі рухаються таким чином, що даний момент весь час змінюється, але швидкості електрона такі великі, що практично визначається середнє значення даного моменту. Тому надалі під дипольним моментом молекули будемо розуміти для електронів
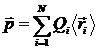 (4.2)
(4.2)
і для ядер: 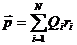 .
.
Інакше кажучи, будемо вважати, що електрон знаходиться відносно ядер у спокої в деяких точках, отриманих усередненням положень електрона по часу.
Поведінка молекули в зовнішньому електричному полі також визначається її дипольним моментом. В цьому можна пересвідчитись розрахувавши потенціальну енергію молекули в зовнішньому електричному полі.
Виберемо початок координат всередині молекули і скористуємось малим значенням 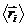 . Тоді потенціал в точці, де знаходиться і-тий заряд можна представити
. Тоді потенціал в точці, де знаходиться і-тий заряд можна представити
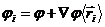 ,
,
де φ – потенціал поля а початку координат.
Тоді, потенціальна енергія визначається як сума:
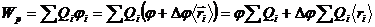 .
.
Враховуючи закон збереження зарядів, 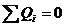 і
і 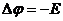 , маємо
, маємо
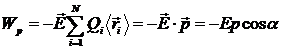 .
.
Якщо продиференціювати вираз по куту, то отримаємо рівняння для обертального моменту. Взявши потім похідну по dx – отримаємо силу.
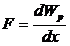 .
.
Таким чином, молекула як по відношенню до поля, яке вона створює, так і по відношенню до тих сил, що діють на неї у зовнішньому полі, буде мати еквівалентні диполі. Позитивний заряд даного диполя дорівнює сумарному заряду ядер і розміщений в „центрі тяжіння” позитивних зарядів, а негативний заряд дорівнює сумарному заряду електронів і розміщений в „центрі тяжіння” негативних зарядів.
В симетричних молекулах (H2, O2, N2 і т.д.) у відсутності зовнішнього електричного поля центри тяжіння позитивних і негативних зарядів співпадають. Такі молекули не володіють власним дипольним моментом і називаються неполярними молекулами.
В несиметричних молекулах (CO, NH, HCl) центри тяжіння зарядів різних знаків зміщені один відносно одного і молекули володіють власним дипольним моментом. Такі молекули називаються полярними.
Під дією зовнішнього електричного поля заряди в неполярних молекулах зміщуються один відносно одного – позитивний заряд за напрямком поля, а негативний – проти поля. В результаті молекула набуває дипольного моменту, величина якого пропорційна напруженості поля. В раціоналізованій системі коефіцієнти пропорційності – ε0, β (ε0 – електростатична стала, β – поляризованість молекули).
Враховуючи, що вектори 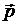 і
і 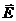 колінеарні, можна записати
колінеарні, можна записати
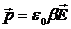 . (4.3)
. (4.3)
Процес поляризації неполярних молекул протікає так, ніби позитивні і негативні заряди зв’язані пружними силами. Тому кажуть, що неполярна молекула веде себе у зовнішньому полі як пружний диполь. Тоді дія зовнішнього поля на полярну молекулу зводиться до того, щоб повернути молекулу так, щоб її дипольний момент встановився за напрямом поля. На величину даного моменту зовнішнє поле практично не діє. Відповідно, полярна молекула веде себе в зовнішньому полі як жорсткий диполь.
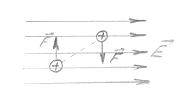
Рис.4.1
4.2. Поляризація діелектриків
За відсутності зовнішнього поля сумарний дипольний момент молекули дорівнює нулю.
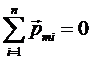 .
.
Під дією зовнішнього поля діелектрик поляризується. Це означає, що результуючий дипольний момент діелектрика стає відмінним від нуля. Характеризує ступінь поляризованості дипольний момент одиниці об’єму.
Якщо зовнішнє електричне поле неоднорідне, то ступінь поляризації в різних точках може бути різний. Щоб охарактеризувати поляризованість в даній точці треба виділити фізично нескінченно малий об’єм, який включає в себе дану точку, знайти суму всіх дипольних моментів, які знаходяться в даному об’ємі, і взяти відношення
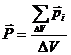 , (4.4)
, (4.4)
де 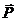 – поляризованість діелектрика.
– поляризованість діелектрика.
У ізотропних діелектриків поляризованість пов’язана з напруженістю поля в цій точці співвідношенням
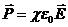 , (4.5)
, (4.5)
де χ – діелектрична сприйнятливість діелектрика (величина безрозмірна, незалежна від напруженості Е).
Або в системі Гауса:
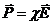 . (4.6)
. (4.6)
Для діелектриків, що побудовані з неполярних молекул, рівняння (4.5) випливає з міркувань:
- в межах об’єму ∆V попадає кількість молекул n∆V(n– число молекулв одинці об’єму);
- кожен з дипольних моментів визначається за формулою (4.3) і тоді сума всіх цих дипольних моментів рвизначається за формулою
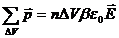 .
.
Якщо розділити на ∆V отримаємо поляризованість (за означенням).
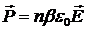 .
.
Позначивши 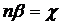 , отримаємо формулу (4.5).
, отримаємо формулу (4.5).
У випадку діелектриків з полярними молекулами орієнтуючій дії зовнішнього поля протидіє тепловий рух молекул, який прагне розкидати їх дипольні моменти по всім напрямкам, в результаті чого встановлюється деяка переважна орієнтація дипольних моментів в напрямку поля. Поляризованість буде пропорційна напруженості поля – формула (4.5). Діелектрична сприйнятливість χ таких діелектриків обернено пропорційна абсолютній температурі середовища.
В іонних кристалах окремі молекули втрачають свою обособленість і весь кристал представляє собою одну дуже велику молекулу. Решітку іонного кристалу можна розглядати як дві решітки, одна з яких вставлена в іншу. Тоді одна з них утворена позитивними, а інша негативними іонами.
Якщо зовнішнє поле буде діяти на іони кристалу, то ці решітки будуть переміщуватись одна відносно одної, що призведе до поляризації діелектрика. Поляризованість буде зв’язана з напруженістю поля рівнянням (4.5).
Пряма залежність напруженості поля і ступеня поляризованості молекули має місце лише в не дуже сильних полях. Це ж стосується рівняння (4.3).
4.3. Опис векторного поля в діелектриках
Всі заряди, які входять в склад молекули діелектрика називаються зв’язаними. Під дією поля зв’язані заряди можуть лише трохи зміщуватись з положення рівноваги, покинути межі своїх молекул зв’язані заряди не можуть.
Заряди, які хоча і знаходяться в межах діелектрика, але не входять в склад його молекули, а також заряди, розташовані за межами діелектрика називаються сторонніми (вільними) зарядами.
Поле в діелектрику є суперпозицією полів сторонніх і зв’язаних зарядів. Результуюче поле називаєтьсямікроскопічним або істинним .
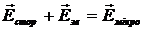 . (4.7)
. (4.7)
Мікроскопічне поле досить сильно змінюється в межах міжмолекулярних відстаней. Внаслідок руху зв’язаних зарядів дане мікроскопічне поле змінюється також у часі. При макроскопічному розгляді дані зміни не спостерігаються, тому в якості характеристики поля використовують середнє по фізично нескінченно малому об’єму значення формули (7), тобто
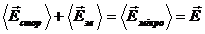 .
.
Надалі, 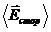 позначимо
позначимо 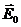 , а
, а 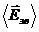 –
– 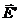 . Відповідно, макроскопічним полем будемо називати величину
. Відповідно, макроскопічним полем будемо називати величину
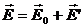 . (4.8)
. (4.8)
Поляризованість представляє собою макроскопічну величину, тому під напруженістю в формулі (4.5) потрібно розуміти напруженість за формулою (4.8). При відсутності діелектриків (у вакуумі) макроскопічне поле чисельно дорівнює полю сторонніх зарядів Ео
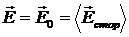 .
.
Якщо сторонні заряди нерухомі, то поле визначається виразом (4.8) і володіє такими ж властивостями як електростатичне поле у вакуумі. Тобто його можна охарактеризувати за допомогою потенціалу φ, що зв’язаний з напруженістю Е через градієнт 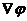 .
.
4.4 Сегнетоелектрики
Існує група речовин, які володіють самочинною поляризованістю при відсутності зовнішнього поля. Це явище було відкрито для сегнетової солі.
Сегнетоелектрики відрізняються наступними характерними особливостями:
1. В той час, коли у діелектриків величина діелектричної проникливості середовища складає декілька одиниць (за винятком деяких речовин, у яких вона сягає декількох десятків, наприклад, для води – ε=81), то ε сегнетоелектриків буває порядку кількох тисяч.
2. Залежність поляризованості від напруженості не є лінійною; відповідно ε є залежною від напруженості.
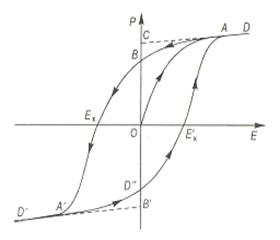 3. При зміні поля значення поляризованості, а відповідно і значення діелектричного зміщення відстають від напруженості, внаслідок чого і Р, і D визначаються не лише величиною Е в даний момент, а і тими значеннями Е,які їй передують, тобто залежить від передісторії даного діелектрика. Це явище називається гістерезисом(від грецького „запізнення).
3. При зміні поля значення поляризованості, а відповідно і значення діелектричного зміщення відстають від напруженості, внаслідок чого і Р, і D визначаються не лише величиною Е в даний момент, а і тими значеннями Е,які їй передують, тобто залежить від передісторії даного діелектрика. Це явище називається гістерезисом(від грецького „запізнення).
При циклічних змінах поля залежність поляризованості від напруженості потрібно зображати, так званою, петлею гістерезису.
Якщо спочатку ввімкнене електричне поле напруженістю Е буде рости до певного значення Р при відповідномуЕ – маємо криву OD на рис. 4.2.
Рис. 4.2
Зменшення Р буде відбуватись зі зменшенням Е по лінії DBEK 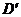 . При значенні Е=0 речовина зберігає значення Рr, що називається залишковою поляризованістю.
. При значенні Е=0 речовина зберігає значення Рr, що називається залишковою поляризованістю.
Лише під дією протилежно направленого поля напруженості Есполяризованість стає рівною нулю. Це значення Е називається коерцитивною силою. При подальшій зміні напруженості отримаємо гілку 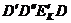 петлі гістерезисну і т.д.
петлі гістерезисну і т.д.
Поведінка вектора поляризованості сегнетоелектриків аналогічна до поведінки вектора намагніченості феромагнетиків, тому їх називають фероелектриками.
Сегнетоелектриками можуть бути кристалічні речовини, у яких відсутній центр симетрії. Взаємодія частинок в кристалі сегнетоелектрика призводить до того, що їх дипольні моменти спонтанно встановлюються в деякому напрямку. Як правило, в кристалі виникають області, в межах кожної з яких дипольні моменти паралельні один одному, але напрям поляризованості різних областей є різним, так що результуючий момент всього кристалу може дорівнювати нулю. Області самовільної поляризації називаються доменами. Під дією зовнішнього поля моменти доменів повертаються як ціле і встановлюються в напрямі поля.
Для кожного сегнетоелектрика існує температура, при якій він втрачає свої властивості і стає звичайним діелектриком. Ця температура називається точкою Кюрі.
Для сегнетової солі точки Кюрі – мінус 15оС і плюс 22оС, тобто сіль веде себе як сегнетоелектрик лише в інтервалі температур від мінус 15оС до плюс 22оС .
4.5. Умови на межі двох діелектриків
На межі двох середовищ з різними дieлeктpичними влacтивocтями вeктopи eлeктpичнoгo пoля змінюються за знaчeнням i нaпpямoм. Умoви пoвeдiнки вeктopiв 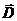 і
і 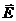 нa мeжi поділу cepeдoвищ нaзивaють гpaнuчнuмu. Ці умoви отримують із ocнoвних рівнянь пoля. Bcтaнoвимo cпoчaтку rpaничнi умови для нopмaльнoї cклaдoвoї вектора
нa мeжi поділу cepeдoвищ нaзивaють гpaнuчнuмu. Ці умoви отримують із ocнoвних рівнянь пoля. Bcтaнoвимo cпoчaтку rpaничнi умови для нopмaльнoї cклaдoвoї вектора 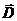 . Для цьoro використаємо рівняння
. Для цьoro використаємо рівняння 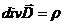 , aбo в iнтeгpaльнiй фopмi для випадку пoвepхнeвoгo poзпoдiлу вільних зapядiв
, aбo в iнтeгpaльнiй фopмi для випадку пoвepхнeвoгo poзпoдiлу вільних зapядiв 
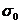
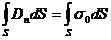 .
.
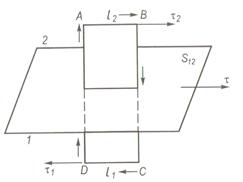
Нехай дано поверхню поділу S12 діелектриків 1 і 2 з діелектричними проникностями е1 і е2 (рис.4.3). Виділимо на пoвepхнi S12 eлeмeнтapну площу S0, у межах якої пoвepхневу густину вiльних зapядiв мoжнa вважати oднaкoвoю ( 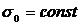 ).
).
Побудуємо навколо S0 замкнену, нaпpиклaд цилiндpичну, пoвepхню і визнaчимo потік вeктopa індукції поля D, cтвopeнoro зapядaми у0, крізь циліндричну пoвepхню S. Пocтaвимo нopмaлi до зoвнiшнiх частин пoвepхoнь S12, S1, Sг. Toдi
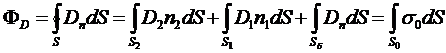 .
.
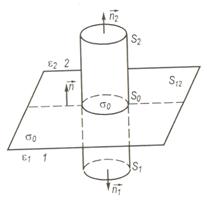 Оскільки
Оскільки 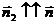 , a
, a 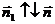 , то D2n2=D2n, a D1n1= -D1n.
, то D2n2=D2n, a D1n1= -D1n.
Для знaхoджeння rpaничних умов на мeжi поділу середовищ 1 і 2 пpиймeмo, що виcoтa циліндра  . Пpи цьому
. Пpи цьому 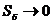 i, отже,
i, отже, 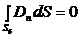 . Значення D2 і D1, у місцях poзтaшувaння поверхонь S1 і Sг ввaжaтимeмo сталими, тому їх можна вивести з-під знаків iнтerpaлiв. Після iнтeгpувaння за вiдпoвiдними пoвepхнями oдepжимo
. Значення D2 і D1, у місцях poзтaшувaння поверхонь S1 і Sг ввaжaтимeмo сталими, тому їх можна вивести з-під знаків iнтerpaлiв. Після iнтeгpувaння за вiдпoвiдними пoвepхнями oдepжимo
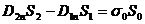 .
.
Рис. 4.3
Приймемо 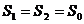 , тoдi
, тoдi
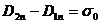 .
.
Це i є гpaничнa умова для нopмaльнoї cклaдoвoї вeктopa індукції eлeк-тpocтaтичнoгo поля D. Як видно, при пepeхoдi мeжi поділу двох дieлeктpикiв значення нopмaльнoї cклaдoвoї вeктopa D cтpибкoм змiнюeтьcя на вeличину у0. Якщо у0= 0 (вільних зарядів на мeжi поділу немає), то 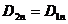 , тобто нopмaльнa cклaдoвa вeктopa D не змінюється. Hopмaльнa ж cклaдoвa вeктopa нaпpужeнocтi eлeктpичнoгo поля Е при цьому змінюється i poзмip цієї змини залежить від cпiввiднoшeння дieлeктpичних пpoникнocтeй середовищ ε1 і ε2 . Cпpaвдi,
, тобто нopмaльнa cклaдoвa вeктopa D не змінюється. Hopмaльнa ж cклaдoвa вeктopa нaпpужeнocтi eлeктpичнoгo поля Е при цьому змінюється i poзмip цієї змини залежить від cпiввiднoшeння дieлeктpичних пpoникнocтeй середовищ ε1 і ε2 . Cпpaвдi, 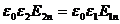 . Звідси
. Звідси
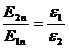 . (4.9)
. (4.9)
На межі провідника і діелектрика з поверхневим розподілом вільних зарядів q0 гранична умова визначається формулою (4.9). Якщо вважати середовище 1 провідником, то, як відомо, в ньому El =0, тому Dln =0 і, отже 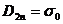 , або
, або 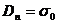 . Відповідно для нормальної складової напруженості Е поля
. Відповідно для нормальної складової напруженості Е поля
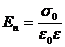 . (4.10)
. (4.10)
У випадку контакту провідника з вакуумом (ε = 1)
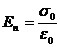 . (4.11)
. (4.11)
 З рівностей (4.10) і (4.11) видно, що напруженість електричного поля біля поверхні провідника за наявності діелектрика зменшується в ε разів. Формула (4.10) дає фактично безпосередній розв’язок задачі про поле в плоскому контурі. При цьому в явному вигляді не довелося враховувати поверхневих зарядів у діелектрику між обкладками конденсатора.
З рівностей (4.10) і (4.11) видно, що напруженість електричного поля біля поверхні провідника за наявності діелектрика зменшується в ε разів. Формула (4.10) дає фактично безпосередній розв’язок задачі про поле в плоскому контурі. При цьому в явному вигляді не довелося враховувати поверхневих зарядів у діелектрику між обкладками конденсатора.
Рис.4.4
Виведемо граничні умови для тангенціальної складової вектора Е, тобто простежимо, як поводить себе дотична складова вектора Е до поверхні поділу двох діелектриків.
Побудуємо поблизу межі поділу діелектриків 1 і 2 замкнений контур ABCD (рис. 4.4). Оскільки електростатичне поле є потенціальним, то циркуляція вектора напруженості дорівнює нулеві:
 . (4.12)
. (4.12)
Для замкненого контура ABCDA з формули (4.12) маємо
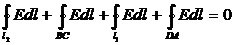 . (4.13)
. (4.13)
Щоб одержати граничну умову для тангенціальної складової вектора Е на межі поділу середовищ, спрямуємо висоту AD = BC обраного контур до нуля. Тоді

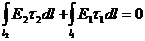 . (4.14)
. (4.14)
Оскільки 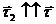 , а
, а 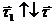 , то
, то  і
і 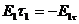 . Тоді вираз (4.13) запишеться так:
. Тоді вираз (4.13) запишеться так: 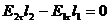 . Якщо l1= l2= l , то одержимо
. Якщо l1= l2= l , то одержимо
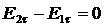 . (4.15)
. (4.15)
Звідси видно, що тангенціальна складова вектора напруженості електростатичного поля не змінюється при переході межі поділу двох середовищ з різними діелектричними властивостями: 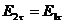 .
.
Якщо взяти межу поділу провідника (середовище 1) і діелектрика (середовище 2), то при цьому 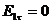 (всередині провідника поле відсутнє) і, отже
(всередині провідника поле відсутнє) і, отже 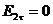 . Це означає, що вектор нaпpужeнocтi eлeктpoстатичного поля завжди перпендикулярний до межі поділу провідник – діелектрик, або провідник – вакуум.
. Це означає, що вектор нaпpужeнocтi eлeктpoстатичного поля завжди перпендикулярний до межі поділу провідник – діелектрик, або провідник – вакуум.
З умов 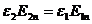 і
і 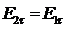 видно, що при ε1< ε2
видно, що при ε1< ε2 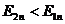 , тобто силові лінії електростатичного поля заломлюються, відхиляючись більше від нормалі при переході в середовище з більшою діелектричною проникністю. Виведемо закон заломлення силових ліній поля.
, тобто силові лінії електростатичного поля заломлюються, відхиляючись більше від нормалі при переході в середовище з більшою діелектричною проникністю. Виведемо закон заломлення силових ліній поля.
Зрис. 4.4 видно, що 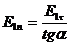 , а
, а 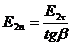 . Взявши до уваги рівності
. Взявши до уваги рівності 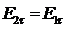 і
і  , одержимо
, одержимо
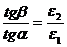 . (4.16)
. (4.16)
Лекція 5
Дата добавления: 2018-05-09; просмотров: 424; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
