Метод ветвей и границ для задачи целочисленного программирования.
Рассмотрим частично целочисленную задачу ЛП:
минимизировать
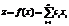 (10.23)
(10.23)
при условиях
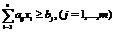 ; (10.24)
; (10.24)
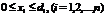 ; (10.25)
; (10.25)
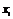 - целые числа. (10.26)
- целые числа. (10.26)
Процесс поиска оптимального решения начинают с решения непрерывной задачи ЛП. Если полученный при этом оптимальный план 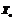 не удовлетворяет условию (10.26), то значение целевой функции
не удовлетворяет условию (10.26), то значение целевой функции 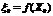 дает нижнюю оценку для искомого решения, т.е.
дает нижнюю оценку для искомого решения, т.е. 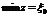 .
.
27.Опишите процесс решения задач линейного программирования с использованием программного обеспечения MATLAB
В состав MATLAB входит Optimization Toolbox, предназначенный для решения линейных и нелинейных оптимизационных задач.
Задача линейного программирования состоит в нахождении вектора x, который минимизирует целевую линейную функцию
fTx при условии AX≤B ; X≥0,
где с=(с1, c2,…,cn) представляет собой n-мерный вектор, соствленный из коэффициентов целевой функции, причем cT – транспонированная вектор- строка; x=(x1 . xn) – n –мерный вектор переменных решений,
B=[b1
b2 m-мерный вектор свободных членов
bm]
Beq=[beq1
…
beqr] ограничения в виде равенств;
двусторонние покомпонентные ограничения в векторной форме
lb≤x≤ub
A= 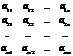
Пример: задача состваления рациона питания
Имеются 3 продукта П1, П2 и П3 разной цены, каждый из которых содержит определенное количество питательных ингридиентов И1, И2, И3, И4.
Известно, что в день требуется : И1не менее 250, И2 не менее 60, И3 не менее 100 и И4 не менее 220. Требуется минимизировать затраты на приобретение продуктов. Очевидно, что количество приобретаемых процессов не может быть отрицательным..
|
|
|
Записываем целевую функцию, матрицу A, векторы b и lb в соответствии с требованиями Toolbox, обозначив искомые количества продуктов через x1, x2 и x3 соответственно. Поскольку линейные ограничения содержат «меньшк или равно», а количество ингредиентов в рационе не может быть менее заданных величин, то следует изменить знаки обеих частей системы.При вызове программы linprog вместо неиспользуемых ограничение (нет ограничений в виде равенств) задайте пустые массивы, обозначаемые в MATLAB пустыми скобками.
Программа ration
% задание матрицы и вектора правой части системы неравенств
A=[4 6 15
2 2 0
5 3 4
7 3 12]
A=-A; b=[250 60 100 220]; b=-b;
% Определение коэффициентов целеой функции f=[44; 35; 100];
% Задание ограничений снизу на переменные lb=[0; 0; 0];
% решение и вывод результата в командное окно x=linprog(f,A,b,[],[],lb)
31.Опишите алгоритм решения задач дискретного программирования методом ветвей и границ
Метод ветвей и границ для задачи целочисленного программирования.
Рассмотрим частично целочисленную задачу ЛП:
минимизировать
|
|
|
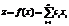 (10.23) при условиях
(10.23) при условиях
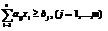 (10.24)
(10.24) 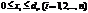 ; (10.25)
; (10.25)
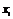 - целые числа. (10.26)
- целые числа. (10.26)
Процесс поиска оптимального решения начинают с решения непрерывной задачи ЛП. Если полученный при этом оптимальный план 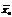 не удовлетворяет условию (10.26), то значение целевой функции
не удовлетворяет условию (10.26), то значение целевой функции 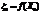 дает нижнюю оценку для искомого решения, т.е.
дает нижнюю оценку для искомого решения, т.е. 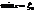 . Пусть некоторая переменная хi0 (1≤ i0 ≤ т) не получила в плане
. Пусть некоторая переменная хi0 (1≤ i0 ≤ т) не получила в плане 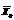 целочисленного решения. В целочисленном плане значение хi0 следует либо уменьшить, по крайней мере до [хi0], либо увеличить, по крайней мере до [хi0]+ 1. Если границы изменения хi0 заранее не заданы, то их можно вычислить, решив для этого две вспомогательные задачи ЛП. Эти задачи состоят в максимизации и минимизации хi0 при условиях (10.24) и (10,25).
целочисленного решения. В целочисленном плане значение хi0 следует либо уменьшить, по крайней мере до [хi0], либо увеличить, по крайней мере до [хi0]+ 1. Если границы изменения хi0 заранее не заданы, то их можно вычислить, решив для этого две вспомогательные задачи ЛП. Эти задачи состоят в максимизации и минимизации хi0 при условиях (10.24) и (10,25).
Теперь для каждого фиксированного целочисленного значения хi0 в найденном отрезке [хi0min, хi0max] находят min z, решая задачу ЛП с ограничениями (10.24), (10.25) и с дополнительным ограничением хi0≤ki0..
Таким образом, все указанные выше возможности можно представить в виде некоторого дерева, в котором вершина 0 отвечает плану 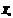 , а каждая из соединенных с ней вершин отвечает оптимальному плану следующей задачи: минимизировать z при условиях (10.24), (10.25) и дополнительном условии, что переменной хi0 дано значение хi0 ≤ кi0, где кio - целое число. Каждой из таких вершин приписывают оценку , которая равна min z при указанных выше ограничениях. Очевидно,
, а каждая из соединенных с ней вершин отвечает оптимальному плану следующей задачи: минимизировать z при условиях (10.24), (10.25) и дополнительном условии, что переменной хi0 дано значение хi0 ≤ кi0, где кio - целое число. Каждой из таких вершин приписывают оценку , которая равна min z при указанных выше ограничениях. Очевидно,  , для всех k. Если оптимальные планы полученных задач удовлетворяют условиям целочисленности, то план с минимальной оценкой
, для всех k. Если оптимальные планы полученных задач удовлетворяют условиям целочисленности, то план с минимальной оценкой 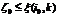 и будет оптимальным планом исходной задачи. В противном случае возникает необходимость в продолжении ветвления. При этом каждый раз для очередного ветвления выбирают вершину с наименьшей оценкой. Любой маршрут в дереве от начальной вершины 0 до некоторой вершины определяет допустимую последовательность выбора целочисленных решений для переменных. Процесс продолжают до тех пор, пока продолжение ветвления становится невозможным. Каждая конечная вершина отвечает некоторому допустимому целочисленному плану. Вершина с минимальной оценкой дает оптимальный план. Рассмотрим алгоритм решения задачи целочисленного программирования.
и будет оптимальным планом исходной задачи. В противном случае возникает необходимость в продолжении ветвления. При этом каждый раз для очередного ветвления выбирают вершину с наименьшей оценкой. Любой маршрут в дереве от начальной вершины 0 до некоторой вершины определяет допустимую последовательность выбора целочисленных решений для переменных. Процесс продолжают до тех пор, пока продолжение ветвления становится невозможным. Каждая конечная вершина отвечает некоторому допустимому целочисленному плану. Вершина с минимальной оценкой дает оптимальный план. Рассмотрим алгоритм решения задачи целочисленного программирования.
|
|
|
На первом этапе необходимо задать множество G(0), определяемое условиями (10,24), (10.25). На втором этапе формируются множества 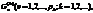 задаваемые условиями (10.24), (10.25) и дополнительным условием xj≤[xj0] или xj≥[ xj0] +1 (10.27) где [xj0]- целая часть хj0. На третьем этапе осуществляется вычисление оценок. Для множества G(0) оценку
задаваемые условиями (10.24), (10.25) и дополнительным условием xj≤[xj0] или xj≥[ xj0] +1 (10.27) где [xj0]- целая часть хj0. На третьем этапе осуществляется вычисление оценок. Для множества G(0) оценку 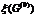 определяют как
определяют как 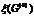 =f(
=f( 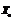 ), где
), где 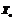 - оптимальный план непрерывной задачи ЛП. Для множества
- оптимальный план непрерывной задачи ЛП. Для множества 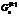 оценку
оценку 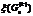 определяют аналогично:
определяют аналогично: 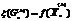 ,где
,где 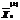 -оптимальный план задачи с условиями (10.24), (10.25) и с дополнительным условием (10.27). Если множество
-оптимальный план задачи с условиями (10.24), (10.25) и с дополнительным условием (10.27). Если множество 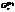 оказывается пустым, ему приписывают оценку
оказывается пустым, ему приписывают оценку 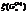 =∞. На четвертом этапе осуществляется нахождение планов. Если план
=∞. На четвертом этапе осуществляется нахождение планов. Если план 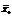 удовлетворяет условию целочисленности (10.26),
удовлетворяет условию целочисленности (10.26), 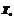 -оптимальный план задачи. Если
-оптимальный план задачи. Если 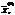 удовлетворяет условию целочисленности (10.26), он яв-ся оптимальным планом задачи с условиями (10.24), (10.25), (10.27) и некоторым планом исходной задачи (10.23) - (10.26). На пятом этапе выполняют ветвление. Ветвление производят в том случае, когда план
удовлетворяет условию целочисленности (10.26), он яв-ся оптимальным планом задачи с условиями (10.24), (10.25), (10.27) и некоторым планом исходной задачи (10.23) - (10.26). На пятом этапе выполняют ветвление. Ветвление производят в том случае, когда план 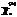 не удовлетворяет условию целочисленности (10.26). Пусть
не удовлетворяет условию целочисленности (10.26). Пусть 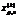 - одна из нецелочисленных компонент плана, где 1 ≤ρ≤n1, тогда множество
- одна из нецелочисленных компонент плана, где 1 ≤ρ≤n1, тогда множество 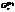 разбивают на два подмножества:
разбивают на два подмножества:
|
|
|
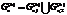 .причем
.причем 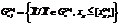 ; (10.28)
; (10.28) 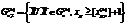 (10.29)
(10.29)
32.Дайте общую математическую формулировку задач нелинейного программирования
Нелинейное программирование- раздел теории оптимизации (теории экстремальных задач), посвященный исследованию и решению задач минимизации (максимизации), в которых целевая функция и ограничения не яв-ся линейными. К нелинейному программированию относят квадратичное , дробное, выпуклое , дискретное , целочисленное и геометрическое программирование.
В общем виде задачу нелинейного программирования можно сформулировать так:
F (х)→min (max) (1) при условии g(x)≤ 0, (2)
где х - вектор искомых переменных; F (х) - целевая числовая функция; g(x) - вектор-функция системы ограничений.
При этом могут быть разные случаи: целевая функция - нелинейная, а ограничения - линейны; целевая функция - линейная, а ограничения (хотя бы одно из них) - нелинейные; целевая функция и ограничения нелинейные. Задачи условной оптимизации нелинейного программирования бывают двух типов: когда в ограничениях (2) имеют место а) знаки равенства б) знаки неравенства.
Решение задачи нелинейного программирования (поиск глобального минимума или максимума) состоит в отыскании таких значений переменных, подчиненных системе ограничений, при которых достигает минимума или максимума данная целевая функция.
При решении некоторых нелинейных задач иногда удается использовать линейную теорию. Для этого вводят допущение, что на том или ином участке целевая функция возрастает или убывает пропорционально изменению переменных. Такой подход называется методом кусочно-линейных приближений.
Нелинейные задачи с ограничениями в форме равенств нередко решаются с помощью введения функции Лагранжа.
Функция Лагранжа для функции 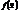 имеет вид:
имеет вид: 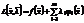 , где
, где 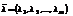 - вектор множителей Лагранжа.
- вектор множителей Лагранжа.
Среди большого числа вычислительных алгоритмов нелинейного программирования значительное место занимают различные варианты градиентных методов (метод проекции градиента, метод условного градиента и т. п.), методы штрафных функций, методы барьерных функций, метод модифицированных функций Лагранжаи др.
Универсального метода, позволяющего находить наиболее эффективным способом решение любой нелинейной задачи, не существует. Поэтому для каждой конкретной задачи, учитывая ее специфику, подбирают тот или иной наиболее подходящий метод (и алгоритм) решения.
28.Дайте общую формулировку задач дискретного программирования
Постановка задачи дискретного программирования.Многиезадачи системного анализа, такие как распределение ресурсов, задачи сетевого планирования и управления, календарного планирования, описываются математическими моделями дискретного программирования.
Рассмотрим общую задачу максимизации.
Найти 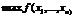 при условиях
при условиях
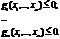
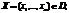 (10.12)
(10.12)
где D - некоторое множество R(n)
Если множество D яв-ся конечным или счетным, то условие (10.12) - это условие дискретности, и данная задача яв-ся задачей дискретного программирования (ЗДП). Чаще всего условие дискретности разделено по отдельным переменным следующим образом:
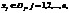
где D - конечное (или счетное) множество.
Если вводится ограничение х; - целые числа (j=l,2,..., n), то приходят к задачам целочисленного программирования (ЦП), которое яв-ся частным случаем дискретного программирования.
В задачах дискретного программирования область допустимых решений яв-ся невыпуклой и несвязной. Поэтому отыскание решения таких задач сопряжено со значительными трудностями. В частности, невозможно применение стандартных приемов, используемых при замене дискретной задачи ее непрерывным аналогом, состоящих в дальнейшем округлении найденного решения до ближайшего целочисленного. Например, рассмотрим следующую ЗЛП:
найти max (x1-3x2 +3х3) при условиях
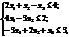
где х1, х2, х3 ≥ 0, xj - целые числа (j = 1,2, 3). Игнорируя условие целочисленности, находим оптимальный план симплекс-методом:
x1опт=1/2, x2=0,…,x2опт=9/2.
Проверка показывает, что никакое округление компонент этого плана не дает допустимого решения, удовлетворяющего ограничениям этой задачи. Искомое целочисленное решение задачи x1пт =2, x2опт=0, x3опт=5.
Таким образом, для решения задачи дискретного программирования (ЗДП) необходимы специальные методы. Методы решения ЗДП по принципу подхода к проблеме делят на три группы: 1) методы отсечения или отсекающих плоскостей; 2) метод ветвей и границ; 3) методы случайного поиска и эвристические методы.
33.Приведите содержательные постановки задач, приводящие к моделям нелинейного программирования
Постановки задач нелинейного программирования. Задачи нелинейного программирования на практике возникают довольно часто, например, когда затраты растут непропорционально количеству закупленных или произведенных товаров. Хорошо известно, что чем больше партия закупаемого товара, тем меньше стоимость единицы продукта. Любому покупателю знакомо понятие розничных и оптовых цен. Рассмотрим конкретный пример, иллюстрирующий данную ситуацию.
Планирование производства продукции. На действующем предприятии планируется организовать выпуск новых видов продукции. Для организации производства необходимо приобретать сырье, стоимость которого колеблется в зависимости от спроса. Цены на готовую продукцию предприятия предполагаются стабильными.
Итак, необходимо провести исследования о производстве двух видов изделий, для которых планируется приобретение сырья, цена которого зависит от объема закупаемой партии и спроса на рынке на сырье данного типа. Цены же на продукцию предприятия утверждены с учетом реальной обстановки и должны сохраняться неизменными. Объемы производства предстоит определить исходя из анализа сырьевой проблемы и ограниченности производственных ресурсов.
Пусть х1, х2 - объемы производимой продукции 1-го и 2-го видов, с1, с2 - цена единицы продукции 1-го и 2-го видов соответственно. Затраты на приобретение и доставку сырья представляют собой нелинейную функцию, зависящую от объема закупаемого товара, f1(x1), f2(x2). Таким образом, экономическая рентабельность планируемых мероприятий оценивается формулой 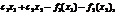 (3)
(3)
Предприятие для производства новых видов продукции может выделить лишь часть своих мощностей, что накладывает дополнительные ограничения на максимальный объем выпуска новых видов изделий. Устанавливаются также лимиты на стоимость основных фондов (эксплуатация зданий, снабжение электроэнергией, амортизационные отчисления) в объеме b1, и стоимость производственных процессов (вспомогательные материалы, заработная плата, накладные расходы и др.) в объеме b2 Известно, что изготовление единицы продукции первого вида требует а11 затрат из основных фондов и а12 трудовых затрат, а единицы продукции второго вида затрат в размере а21 и а22 соответственно. Учет этих факторов приводит к условиям
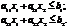 (4)
(4)
Теперь можно сформулировать задачу: определить такие х1, х2, которые бы обеспечивали максимум функционала 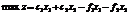 (5)
(5)
при ограничениях 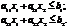 (6) x1 ,x2≤0.
(6) x1 ,x2≤0.
Таким образом сформулирована задача, в которой целевая функция яв-ся нелинейной.
34.Дайте общую математическую формулировку задач квадратичного программирования
Квадратичное программирование- раздел нелинейного программирования, включающий совокупность методов решения экстремальных задач, в которых целевая функция представляет собой многочлен второй степени, а ограничения - линейные функции.
Задача квадратичного программирования может быть записана в матричной форме следующим образом: 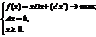 (7) где х - n-мерный вектор-столбец; х' - n-мерная вектор-строка; с' - n-мерная вектор-строка; b -m-мерный вектор-столбец; А - матрица размера т×п; D - симметрическая квадратная матрица порядка n;
(7) где х - n-мерный вектор-столбец; х' - n-мерная вектор-строка; с' - n-мерная вектор-строка; b -m-мерный вектор-столбец; А - матрица размера т×п; D - симметрическая квадратная матрица порядка n;
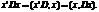 (8)
(8)
Решить задачу квадратичного программирования это значит найти точку 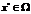 , для которой достигается максимум функции
, для которой достигается максимум функции 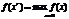 , (9) где Ώ - множество допустимых планов задачи, определяемое системой ограничений
, (9) где Ώ - множество допустимых планов задачи, определяемое системой ограничений
Ах= b, х> 0 . (10)
Если D = 0, то задача сводится к задаче линейного программирования . Если целевая функция задачи квадратичного программирования ограничена сверху, то задача обязательно имеет оптимальное решение, т.е. точку глобального максимума.
Для нахождения глобального максимума общей задачи (1) не существует эффективных вычислительных методов.
В настоящее время развиты методы выпуклого квадратичного программирования - раздела выпуклого программирования, который занимается задачами поиска глобального максимума выпуклой квадратичной функции на многогранном множестве. В этом классе задач доказано, что если матрица D яв-ся отрицательно определенной, то целевая функция (7) будет ограничена сверху, и задача (7) будет иметь оптимальное решение, и притом единственное (при условии, что допустимое множество непусто).
Важное место в выпуклом квадратичном программировании занимает двойственная задача.
В соответствии с общим принципом двойственности для задачи (7) двойственная задача имеет вид:
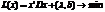 (11)
(11)
при условиях 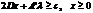 , (12)
, (12)
где A’ - матрица, транспонированная по отношению к А; с - n-мерный вектор-столбец; λ - m-мерный вектор-столбец.
В линейном случае (при D = 0) определение двойственной задачи (11) - (12) совпадает с принятым в линейном программировании.
Как и в случае линейного программирования в квадратичном программировании имеет место теорема двойственности:
Дата добавления: 2018-05-09; просмотров: 718; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
