ТЕМА 4. СТАТИСТИЧНІ ПОКАЗНИКИ
1. Види, типи та значення статистичних показників
2. Абсолютні та відносні величини
3. Середні величини
4. Показники варіації
Види, типи та значення статистичних показників
Після зведення та групування даних спостереження переходять до останнього - третього етапу статистичної методології. Він полягає в подальшій обробці статистичних таблиць шляхом обчислення статистичних показників.
Статистичний показник - це узагальнююча характеристика явища або процесу, яка характеризує всю сукупність одиниць обстеження і використовується для аналізу сукупності в цілому. За допомогою статистичних показників вирішується одна з головних задач статистики: визначається кількісна сторона явища чи процесу у поєднанні з якісною стороною. Кількісний бік показника представляється числом з відповідною одиницею виміру для характеристики: розміру явищ (кількості робітників, обсягу товарооборота, капіталу фірми тощо); їх рівнів (наприклад, рівня продуктивності праці робітників); співвідношень (наприклад, між продавцями та іншими категоріями працівників магазину). Якісний зміст показника залежить від суті досліджуваного явища (процесу) і відображається у назві показника (прибутковість, народжуваність тощо).
Показники поділяються на види в залежності від способу їх обчислення, ознак часу, виконання своїх функції.
За способом обчислення розрізняють первинні та похідні показники. Первинні визначаються шляхом зведення та групування даних і подаються у формі абсолютних величин (наприклад, кількість та сума вкладів громадян у банку). Похідні показники обчислюються на базі первинних і мають форму середніх або відносних величин (наприклад, середня заробітна плата, індекс цін).
|
|
|
Серед статистичних показників окрему групу становлять взаємообернені показники - пара характеристик, які існують паралельно і відповідають одному і тому ж явищу (процесу). Це прямий показник х, який змінюється у напрямі зміни явища (наприклад, продуктивність праці за одну одиницю часу), та обернений 1/х у протилежному напрямі (наприклад, трудомісткість одиниці продукції).
За ознакою часу показники поділяються на інтервальні та моментні. Інтервальні характеризують явище за певний період часу (місяць, квартал, рік): наприклад, середньомісячні сукупні витрати на душу населення. Моментні показники характеризують явище за станом на певний момент часу (дату): наприклад, залишок обігових коштів на початок місяця.
За способом виконання своїх функцій розглядають показники, що відбивають обсяг явища, його середній рівень, інтенсивність прояву, структуру, зміну в часі або порівнянні у просторі.
|
|
|
В статистиці використовують декілька різновидів статистичних показників:
• абсолютні та відносні величини;
• середні величини;
• показники варіації.
Щоб статистичні показники правильно характеризували явище, що розглядається, необхідно виконувати такі вимоги:
1) спиратися при їх побудові на положення економічної теорії, статистичну методологію, досвід статистичних робіт;
2) добиватися повноти статистичної інформації як за охопленням одиниць об'єкта, так і за комплексним відображенням усіх сторін процесу, що вивчається;
3) забезпечувати зіставлення статистичних показників за рахунок подібності вихідних даних за часом та у просторі;
4) забезпечувати точність та надійність вихідної інформації для достовірності змісту процесу, що досліджується.
Абсолютні та відносні величини
Абсолютними величинами в статистиці називають кількісні показники, які визначають рівень, обсяг, чисельність розглядаємих суспільних явищ (наприклад, капітал фірми на початок року, посівна площа сільських господарств на даний момент часу, чисельність робітників підприємства у звітному періоді тощо).
За способом вираження розглядаємого явища абсолютні величини розподіляються на індивідуальні та загальні (сумарні). Індивідуальні величини характеризують ознаки окремих одиниць сукупності. Вони є основою зведення та групування статистичних даних (наприклад, розмір заробітної плати окремого робітника, кількість заявок та обсяги попиту на купівлю товару товарної біржі та ін.) Загальними величинами є такі абсолютні показники, які виражають розміри кількісних ознак у всіх одиниць сукупності. їх знаходять при підсумуванні індивідуальних абсолютних величин (наприклад, фонд заробітної плати робітників підприємств району, вартість основних фондів сільськогосподарських підприємств області тощо).
|
|
|
Абсолютні показники можуть виражати розміри, обсяги та рівні суспільних явищ на певний момент або період часу (наприклад, на 01.01.2004 р. чисельність працюючих на підприємстві становила 1380 осіб; виробництво молока у господарстві за 2003 рік дорівнювало 26100 т).
Абсолютні величини - це іменовані числа і в залежності від характеру явища або процесу можуть мати різні одиниці вимірювання: натуральні (кг, м, шт. і т.д.); умовно-натуральні (одна умовна банка консервів, одна умовна одиниця мінеральних добрив і т.д.); трудові (людино-година, людино-день); вартісні (грн., руб., дол. США, євро та ін.).
|
|
|
Абсолютні показники відіграють важливу роль у системі узагальнюючих статистичних показників. В той же час вони не можуть дати достатньо повного уявлення про досліджуване явище. Тому виникає потреба в обчисленні інших узагальнюючих показників - відносних та середніх величин, підґрунтям для яких є абсолютні величини.
Відносні величини - це узагальнюючі кількісні показники, які виражають співвідношення порівнюваних абсолютних величин.
Логічною формулою відносної величини є такий звичайний дріб:

В залежності від величин чисельника та знаменника цього дробу відносні величини можуть бути виражені у таких формах: коефіцієнтах (частках), процентах (%), проміле (%0), про-деціміле (%оо), коли за базу порівняння приймають відповідно 1, 100, 1000, 10000 одиниць.
Різноманітність співвідношень у реальному житті потребує різних за змістом і статистичною природою відносних величин. В залежності від своїх функцій, що виконують відносні величини при проведенні аналізу, ці величини можна класифікувати так:
Відношення однойменних показників:
1) відносні величини динаміки;
2) відносні величини структури;
3) відносні величини координації;
4) відносний показник планового завдання;
5) відносний показник виконання плану;
6) відносні показники порівняння.
Відношення різнойменних показників:
7) відносні величини інтенсивності;
8) відносні величини диференціації.
Відносна величина динаміки
Динамікою у статистиці називають зміну соціально-економічного явища в часі. Відносна величина динаміки характеризує напрям та інтенсивність зміни показника за часом і визначається співвідношенням його значень за два періоди або моменти часу. При цьому базою порівняння може бути змінний попередній рівень (розрахунок ланцюговим способом) або постійний, віддалений за часом рівень (розрахунок базисним способом). Відносні показники динаміки називають темпами зростання. Наприклад, розмір інвестицій у галузь становив у млн. грн..: 2002 р. - 420,0; 2003 р. - 546,0; 2004 р. -573,5. Порівнюючи значення показника, дістанемо темпи зростання інвестицій:
• розрахунок ланцюговим способом: у 2003 р. порівняно з 2002 р.
 , або 130% (інвестиції зросли на 30%)
, або 130% (інвестиції зросли на 30%)
У 2004 р. порівняно з 2003 р.  або 105 %
або 105 %
• розрахунок базисним способом: якщо за базу приймається рівень інвестицій у 2002 р., то у 2003 р. темп зростання буде 1,3, або 130%; у 2004 р. порівняно з базовим рівнем у 2002 р. темп зростання 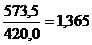 , або 136,5% (інвестиції зросли на 36,5%).
, або 136,5% (інвестиції зросли на 36,5%).
Якщо значення показника у зрівнянні з базовим зменшується, то величина динаміки буде меншою за одиницю.
Відносна величина структури
Статистичні сукупності завжди структуровані і мають певні складові. Відносна величина структури характеризує склад, структуру сукупності за тією чи іншою ознакою і показує внесок складових сукупності до загальної маси. Вона визначається відношенням розмірів складових частин сукупності до загального підсумку. Скільки складових, стільки відносних величин структури. Вони визначаються простим чи десятинним дробом або процентом. Наприклад, частка осіб до працездатного віку міста становить 1/4, або 0,25, або 25%.
Відносна величина координації
Відносна величина характеризує структурованість сукупності. Відносна величина координації дає співвідношення різних структурних одиниць тієї самої сукупності і показує, скільки одиниць однієї частини сукупності припадає на 1, 100, 1000 і більше одиниць іншої, взятої за базу порівняння. Наприклад, частка власних коштів фірми становить 70%, а залучених - 30%.
Тоді відносна величина координації може складати 30/70= 0,43, а це означає, що на одиницю власних коштів припадає 0,43 залучених. Або у іншому прикладі відносна величина координації показує, скільки чоловіків припадає на 1000 жінок або навпаки.
Відносні показники планового завдання та виконання плану
Відносний показник планового завдання - це відношення величин показника, встановленого на плановий період, до його величини, досягнутого за попередній період, який взято за базу зрівняння. Наприклад, на сільськогосподарському підприємстві середньорічний надій від корови у плановому періоді встановлено 3320 кг, за попередній (базисний) рік було 3200 кг. Тоді відносний показник планового завдання дорівнює:
 , тобто у плануємому періоді надій молока очікується на 3,8% більше, чим у базисному періоді.
, тобто у плануємому періоді надій молока очікується на 3,8% більше, чим у базисному періоді.
Відносний показник виконання плану являє собою відношення фактично досягнутого рівня до планового завдання. Наприклад, у періоді, що планується, середньорічний надій молока від корови фактично становив 3480 кг. В такому разі, звертаючись до попереднього прикладу, відносний показник виконання плану становить:  , тобто фактично у розглядаємому періоді надій молока на 4,8% більше плану.
, тобто фактично у розглядаємому періоді надій молока на 4,8% більше плану.
Відносні показники динаміки (К), планового завдання (Кпз) та виконання плану (Квп) зв'язані між собою такими рівняннями: К=Кпз*Квп За нашими прикладами К=1,308*1,048-1,088. Відносний показник динаміки можна обчислити інакше:
Відносні величини порівняння
Відносна величина порівняння у звичайному розумінні характеризує порівняння однойменних показників, що стосуються різних об'єктів, взятих за той самий період чи момент часу. Обчислюється у відносних величинах або процентах. Наприклад, порівняння урожайності пшениці у двох сільськогосподарських підприємствах району у плановому періоді, співвідношення між рівнями собівартості певного виду продукції двох підприємств у звітному періоді тощо.
До цього виду відносних показників належать відносні величини просторового порівняння та відносні величини порівняння зі стандартом.
Відносна величина просторового порівняння - це відношення розмірів або рівнів однойменних показників за різними територіями чи об'єктами. Найчастіше це регіональні чи міжнародні порівняння показників економічного розвитку або життєвого рівня. Базою порівняння може бути будь-який об'єкт. Головне, щоб методика розрахунку порівнюваних показників була однаковою. Наприклад, зіставлення рівнів середньодушових витрат міського та сільського населення, середня очікувана тривалість життя чоловіків і жінок.
Відносна величина порівняння зі стандартом являє собою порівняння фактичних значень показників з певним еталоном - стандартом, нормативом, оптимальним рівнем. Такими відносними величинами порівняння є виконання договірних зобов'язань, використання виробничих потужностей, додержання норм витрат тощо. Наприклад, для проведення своїх операцій фірма повинна тримати в обороті щонайменше 120 тис. грн. Фактично в обороті 108 тис. грн., що становить від потреби 90% (108/120=0,9 або 90%) . Такий показник може привести до невиконання фірмою своїх фінансових зобов'язань і її банкрутства.
Відносна величина інтенсивності
Відносна величина інтенсивності характеризує відношення різнойменних величин, зв'язаних між собою певним чином. Це - щільність населення на
1 кв.км (наприклад, 82,5 осіб/кв.км), виробництво електроенергії на душу населення (наприклад, 5625кВт*год/осіб) тощо. Якщо обсяги явища незначні відносно обсягів середовища, то їх співвідношення збільшуються у 100, 1000, 10000 і більше разів. Наприклад, показники народжуваності, смертності, шлюбності розраховується на 1000 осіб населення, забезпеченість населення лікарями - на 10000 осіб населення, захворюваність та злочинність - на 100000 осіб населення.
Відносна величина диференціації
Відносна величина диференціації обчислюється в результаті порівняння двох структурних рядів, один з яких характеризує співвідношення частин сукупності за чисельністю одиниць, а другий - за величиною будь-якої ознаки (наприклад, порівняння питомої ваги господарств за чисельністю і питомої ваги в цих господарствах валової продукції, основних фондів, працівників тощо).
Середні величини
Середньою величиною в статистиці називаються кількісний показник характерного, типового рівня масових однорідних явищ, який складається під впливом загальних причин і умов розвитку. У зв'язку з цим середні величини відносяться до узагальнюючих статистичних показників, які дають зведену, підсумкову характеристику масових суспільних явищ. В середній величині гасяться (розчиняються) всі відмінності та особливості індивідуальних значень ознак і вона є „рівнодіючою" значень цих ознак. Головними умовами застосування середніх величин є:
1) наявність якісної однорідності сукупності;
2) масовий характер даних сукупності, де діє закон великих чисел.
Залежно від характеру ознаки, що усереднюється, і наявності вихідної статистичної інформації в статистиці використовують декілька видів середніх, серед яких найбільш поширеними є такі: середня арифметична; середня гармонічна; середньо квадратична; середня геометрична. Поряд з переліченими видами середніх величин у статистичній практиці застосовують також середню хронологічну та структурні середні: моду та медіану. Використання того чи іншого виду середніх залежить від двох обставин:
1) від характеру індивідуальних значень ознаки (прямі, обернені, квадратичні, відносні);
2) від характеру алгебраїчного зв'язку між індивідуальними значеннями ознаки та її загального обсягу (сума, добуток, степінь, квадратний корінь).
Кожна із зазначених видів середніх може виступати у двох формах: простої та зваженої. Проста середня застосовується при обчисленні середньої за первинними (не згрупованими) даними, зважена — за згрупованими даними.
При використанні середніх величин введемо такі позначення:
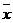 - середнє значення досліджуваної ознаки;
- середнє значення досліджуваної ознаки;
хі або х - кожне індивідуальне значення усереднюваної ознаки (варіанта) в варіаційному ряду;
fi, або f частота повторень (вага) індивідуальної ознаки в варіаційному ряду;
w=хf- обсяг значень ознаки;
n - кількість одиниць досліджуваної ознаки.
Середня арифметична
Середня арифметична - це найпоширеніший вид середньої між інших. Вона застосовується тоді, коли відомі індивідуальні значення усереднюваної ознаки та їх кількість у сукупності. Тоді проста середня арифметична обчислюється діленням загального обсягу значень ознаки на обсяг сукупності:
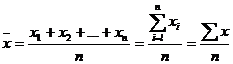
Наприклад, статутний капітал акціонерної компанії сформований 6 засновниками. Розмір внеску кожного з них відповідно становив, млн. грн.: 8; 10; 12; 9; 6; 5. Середній внесок одного засновника розраховується так:
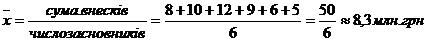
Зважена середня арифметична використовується у тих випадках, коли значення ознаки подано у вигляді варіаційного ряду, в якому чисельність одиниць у варіантах неоднакова. Формула середньої арифметичної зваженої має вигляд:
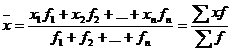
З формули видно, що середня зважена принципово не відрізняється від середньої простої арифметичної. Тут додавання f разів варіанти х змінюється множенням її на кількість повторень (f).
Техніку обчислення середньої арифметичної зваженої проілюструємо прикладом обчислення середньої виробки деталей на одного робітника за зміну, якщо відомо скільки деталей виготовив кожен з 15 робітників.
Таблиця 1
Розподіл робочих за виготовленням деталей
| Виготовлення деталей за зміну одним робітником, шт.. х | Кількість робочих (ваги) f | xf |
| 18 | 2 | 36 |
| 19 | 4 | 76 |
| 20 | 5 | 100 |
| 21 | 3 | 63 |
| 22 | 1 | 22 |
| Всього | 15 | 297 |
За формулою середня арифметична зважена:
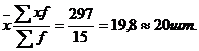
Середня гармонічна
Середня гармонічна - це обернена до середньої арифметичної із обернених значень ознак. її обчислюють, коли необхідно осереднення обернених індивідуальних значень ознак шляхом їх підсумування (наприклад, у випадках визначення середніх витрат часу, праці, матеріалів на одиницю продукції тощо). У випадку розрахунку середньої гармонічної зваженої її обчислюють тоді, коли відомі дані про загальний обсяг ознаки (w=хf), а також індивідуальні значення ознаки (х), невідома є частота (f). Формули середньої гармонічної - простої і зваженої - мають такий вигляд:
Для простої 
Для зваженої 
Для встановлення місця середньої гармонічної в розрахунку середньої величини розглянемо такий приклад. Припустимо, що бригада токарів на протязі 8-годинного робочого дня зайнята обточкою однакових деталей. Перший токар затрачує на одну деталь 12 хв, другий - 15 хв, третій - 11 хв, четвертий -16 хв і п'ятий - 14 хв. Необхідно знайти середній час на виготовлення одної деталі.
На перший погляд, ця задача вирішуються легко за формулою середньої арифметичної простої:
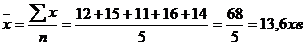
Однак, знайдена середня була би правильною, якщо кожний робітник виробив тільки по одній деталі, а не працював 8 годин, коли робітниками було виготовлено різна кількість деталей. Для розрахунку кількості деталей, виготовлених кожним робітником, використаємо таке співвідношення (логічну формулу):
 =
=
= 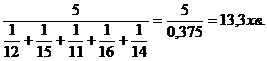
Останнє кількісне співвідношення відповідає формулі середньої гармонічної простої 
Бачимо, що в наявності різниця між результатами обчислення за формулами середньої арифметичної та середньої гармонічної.
Середня квадратична
Середня квадратична використовується для визначення показників варіації (коливання) ознаки - дисперсії та середнього квадратичного відхилення. Обчислюється на основі квадратів відхилень індивідуальних значень ознаки від їх середньої величини. Формула середньої квадратичної має такий вигляд:
Проста 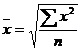
Зважена 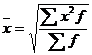
Середня геометрична
Середню геометричну застосовують у тих випадках, коли обсяг сукупності формується не сумою, а добутком індивідуальних значень ознак. Цей вид середньої використовується здебільшого для обчислення середніх коефіцієнтів (темпів) зростання в рядах динаміки. Так, у випадку однакових часових інтервалів між п рівнями динамічного ряду середня геометрична проста має такий вигляд:
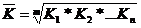
де 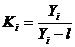 - темпи зростання; уі, уі-l - відповідно звітний та попередній рівні ряду; m- кількість темпів зростання (m=n-1).
- темпи зростання; уі, уі-l - відповідно звітний та попередній рівні ряду; m- кількість темпів зростання (m=n-1).
Прикладом застосування середньої геометричної є наступне. Припустимо, що внаслідок інфляції споживчі ціни за чотири роки зросли в 2,8 рази, в тому числі: за перший рік у 1,7 рази; за другий - в 1,3; за третій - в 1,1; за четвертий - в 1,15 рази. Як визначити середньорічний темп зростання цін? Середня арифметична (1,7+1,3+1,1+1,15):4=1,312 не забезпечує визначеної властивості, так як за чотири роки за цією середньою ціни б зросли у 1,312*1,312*1,312*1,312=2,94 рази, а не в 2,8 рази. Визначену властивість забезпечує тільки середня геометрична:
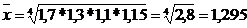
Мода і медіана
Середніми величинами в статистичних рядах розподілу є мода і медіана, які відносяться до класу структурних (позиційних) середніх. їх величини залежать лише від характеру частот, тобто від структури розподілу. На відміну від інших середніх, які залежать від усіх значень ознаки, мода і медіана не залежить від крайніх значень. Це особливо важливо для незакритих крайніх інтервалів варіаційних рядів розподілу.
Мода (Мо) - це значення варіанти, що найчастіше повторюється в ряду розподілу. Спосіб обчислення моди залежить від виду статистичного ряду. Для атрибутивних і дискретних рядів розподілу моду визначають візуально без будь-яких розрахунків за значенням варіанти з найбільшою частотою (часткою). Наприклад, за результатами опитування населення щодо самовизначення матеріального стану за чотирма оцінками (добрий, задовільний, незадовільний, нестерпний) більшість респондентів визначили свій стан як незадовільний - це і буде модою. Або модальною ціною на той чи інший продукт на ринку є та ціна, яка спостерігається найчастіше. В інтервальному ряді спочатку визначається модальний інтервал (інтервал з найбільшою частотою) і значення моди в середні інтервалу розраховується за формулою:
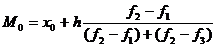
де х0 - нижня межа модального інтервалу;
h - величина модального інтервалу;
f1+f2+f3 - частота відповідно передмодального, модального та післямодального інтервалів.
Медіаною (Ме) називають варіанту, що ділить ранжирований (впорядкований за мірою зростання або зменшення) ряд на дві рівні за обсягом частини. Медіана для дискретного ряду з непарним числом варіант буде відповідати середній варіанті Ме=xm-1, де т - номер кратної варіанти першої половини ранжированного ряду. Медіана для дискретного ряду з парним числом варіант буде відповідати середній із значень варіант у ранжированному ряду
Для інтервального ряду:  медіана обчислюється для середини медіанного інтервалу, за який приймається такий, де сума накопичених частот перевищує половину значень частот ряду розподілу. В даному випадку формула для розрахунку медіани має вигляд:
медіана обчислюється для середини медіанного інтервалу, за який приймається такий, де сума накопичених частот перевищує половину значень частот ряду розподілу. В даному випадку формула для розрахунку медіани має вигляд:
Ме = 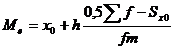
де х0 - нижня межа медіанного інтервалу; h - величина медіанного інтервалу; 0,5∑f - половина суми накопичених частот інтервального ряду; Sx0 — сума накопичених частот перед медіанним інтервалом; fm - частота медіанного інтервалу.
В аналізі закономірностей розподілу використовуються також такі характеристики як квартилі та децилі. Квартилі — це варіанти, які поділяють обсяги сукупності на чотири рівні частини, децилі - на десять частин.
Показники варіації
Після встановлення середньої величини (х,М0,Ме) виникає питання, в якій мірі індивідуальні значення ознаки відрізняються між собою та від середньої. Для цього розраховують показники варіації.
Варіацією ознаки називають різницю у числових значеннях ознак одиниць сукупності та їх коливання навколо середньої величини, що характеризує сукупність. Чим менша варіація, тим одноріднішою є сукупність і більш надійною (типовою) є середня величина.
До основних абсолютних і відносних показників, що характеризують варіацію, є такі: розмах варіації; середнє лінійне відхилення; дисперсія; середнє квадратичне відхилення; коефіцієнт варіації тощо.
Розмах варіації - це різниця між найбільшим та найменшим значеннями ознаки:
R=xmax-xmin
Величина показника залежить тільки від крайніх значень ознаки і не враховує всіх значень, що містяться між ними.
Досконалішим є визначення варіації через інші показники, які дають змогу усунути недолік розмаху варіації.
Середнє лінійне відхилення являє собою середню арифметичну з абсолютних значень усіх відхилень індивідуальних значень ознаки від середньої:
а) просте: 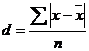
б) зважене: 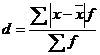
Наявність абсолютних значень відхилень від середньої пояснюється так: середня арифметична має нульову властивість, згідно з якої сума відхилень від середньої індивідуальних значень ознаки зі своїми знаками дорівнює нулю; щоб мати суму всіх відхилень, відмінних від нуля, кожне з них слід брати за абсолютною величиною.
Основним недоліком середнього лінійного відхилення є те, що в ньому не враховуються знаки відхилень, тобто їх спрямованість. Тому цей показник варіації використовується рідко (аналіз складу працюючих, ритмічність виробництва, обертання коштів у зовнішній торгівлі тощо). Показниками варіації, які б усунули недоліки середнього лінійного відхилення, є дисперсія та лінійне квадратичне відхилення.
Дисперсією називають середню арифметичну квадратів відхилень індивідуальних значень ознаки. В залежності від вихідних даних дисперсія може обчислюватись за формулами середньої арифметичної простої або зваженої:
а) проста: 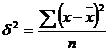
б) зважена: 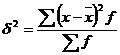
Дисперсія - це один з найбільш розповсюджених в економічній практиці узагальнюючих показників розміру варіації у сукупності. Дисперсію використовують не лише для оцінки варіації, а й для вимірювання зв'язків між досліджувальними факторами; розклад дисперсії на складові дозволяє оцінити вплив різних факторів, які обумовлюють варіацію ознаки.
Середнє квадратичне відхилення, як і дисперсія, виступає в якості широко використовуємого узагальнюючого показника варіації. Його обчислюють, здобувши квадратичний корінь з дисперсії:
а) просте: 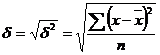
б) зважене: 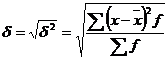
Смислове значення середнього квадратичного відхилення таке саме, як і лінійного відхилення: воно показує, на скільки в середньому відхиляються індивідуальні значення ознаки від їх середнього значення. Перевага цього показника порівняно із середнім лінійним відхиленням полягає у відсутності умовного припущення з підсумування відхилень без врахування їх знаків, бо відхилення використовуються у квадратній степені. Крім зазначеного, перевагою даного показника у зрівнянні з дисперсією є те, що середнє квадратичне відхилення виражається в тих же одиницях вимірювання, що і значення досліджувальної ознаки (грн., кг, га тощо). Тому цей показник називають також стандартним відхиленням.
В статистичній практиці часто виникає необхідність порівняння варіацій різних ознак. Наприклад, великий інтерес має порівняння віку робочих з їх кваліфікацією, стажу роботи з розміром заробітної плати, собівартістю та прибутку і т.і. При таких порівняннях розглянуті показники коливання ознак з різними одиницями вимірювання не можуть бути використані (наприклад, неможливо порівнювати коливання стажу роботи в роках з варіацією заробітної плати в гривнях).
Для здійснення такого роду порівнянь, а також при зіставленні ознаки у декількох сукупностях з різними середніми арифметичними використовують відносний показник варіації - коефіцієнт варіації.
Коефіцієнтом варіації називають процентне відношення середнього квадратичного відхилення до середньої арифметичної величини ознаки:
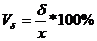
Чим більший коефіцієнт варіації, тим менш однорідна сукупність і тим менш типова середня для даної сукупності. Встановлено, що сукупність кількісно однорідна, якщо коефіцієнт варіації не перевищує 33%.
Дисперсія посідає особливе місце у статичному аналізі соціально-економічних явищ і є важливим елементом статистичних методів, зокрема у дисперсному аналізі.
У структурованій сукупності, яка поділена на т груп за факторною ознакою х, загальна дисперсія σ2 результативної ознаки у, може бути представлена складовими: міжгрупова дисперсія 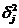 та середня з групових дисперсій сг2 . Згідно з правила розкладання дисперсій має місце рівняння:
та середня з групових дисперсій сг2 . Згідно з правила розкладання дисперсій має місце рівняння:
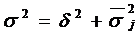
Загальна дисперсія σ2 вимірює варіацію результативної ознаки в цілому за сукупністю під впливом усіх факторів, які обумовлюють цю варіацію. Загальна дисперсія для зваженої результативної ознаки у обчислюється за формулою.
Міжгрупова дисперсія σ2 характеризує варіацію ознаки у за рахунок фактора х, покладеного в основу групування, і розраховується за формулою:
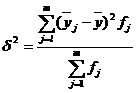
де уj, у - відповідно середня j-ї групи та загальна середня варіюючої ознаки; fj- чисельність одиниць (частота) j-ї групи.
Для розрахунку середньої з групових дисперсій з початку обчислюється внутрішньогрупова дисперсія, яка характеризує варіацію результативної ознаки за рахунок інших факторів, не врахованих у групуванні:
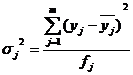
де Уj - значення ознаки окремних елементів сукупності.
Для всіх груп в цілому розраховується середня з групових дисперсій, зважених на частоти відповідних груп:

Користуючись правилом розкладання дисперсій, можна за двома відомими дисперсіями знайти третю - невідому, а також мати уяву про силу впливу групувальної ознаки.
Питання для самоконтролю
1. Означте поняття абсолютної величини та наведіть приклади застосування таких величин у суспільному житті.
2. Назвіть основні види абсолютних величин і наведіть приклади їх застосування.
3. Означте одиниці виміру абсолютних величин. Наведіть приклади натуральних, умовно-натуральних, комбінованих і вартісних одиниць виміру.
4. Опишіть методику переведення продукції в умовно-натуральну на конкретному прикладі.
5. Означте поняття відносної величини. Наведіть приклади обчислення та використання відносних величин.
6. Які одиниці виміру використовують для відносних величин?
7. Як обчислюють відносні величини динаміки й що вони показують?
8. Як обчислюють базисні та ланцюгові відносні величини динаміки? Який взаємозв'язок існує між ними?
9. На конкретному прикладі покажіть, як обчислити базисні величини динаміки на основі ланцюгових.
10. Що таке відносна величина планового завдання (К]із)? Продемонструйте техніку обчислення відносної величини планового завдання та розкрийте її економічний зміст.
11. Як обчислити відносну величину виконання плану (Квм) та що вона показує?
12. Як пов'язані між собою відносні величини динаміки, планового завдання та виконання плану?
13. Якщо заплановано збільшити прибуток фірми на 10%, а фактично збільшили на 15 %, то на скільки відсотків перевиконано план?
14. Які явища можна характеризувати за допомогою відносних величин структури та як обчислювати ці величини?
15. Для характеристики яких явищ застосовують відносні величини інтенсивності?
16. Що виражають відносні величини координації та як їх обчислювати?
17. Для чого служать відносні величини просторового порівняння та як їх обчислювати?
18. Що таке середня величина? Назвіть її недоліки та переваги порівняно з конкретними значеннями ознаки.
19. Яку середню величину вважають огульною середньою?
20. Назвіть основні принципи застосування середніх величин.
21. Які види середніх використовують у статистиці? Назвіть основні види степеневих та позиційних (структурних) середніх.
22. Як обчислюють просту та зважену середню арифметичну?
23. Коли використовують просту та зважену середню арифметичну?
24. Що в статистиці розуміють під варіантою та частотою? Якими символами їх позначають?
25. Як обчислити середню з інтервального ряду розподілу з відкритими інтервалами?
26. Чи можна, обчислюючи середню, використовувати частості замість частот?
27. У чому суть статистичних парадоксів у процесі обчислення середніх?
28. На чому ґрунтуються спрощені способи обчислення середньої арифметичної?
29. Назвіть основні властивості середньої арифметичної.
30. Якщо від кожного конкретного значення ознаки відняти її середнє значення, то сума відхилень буде більша нуля, менша нуля чи дорівнюватиме нулю?
31. Як зміниться середнє значення ознаки, якщо кожне конкретне її значення збільшити чи зменшити на величину а!
32. Як зміниться середнє значення ознаки, якщо кожне конкретне її значення збільшити чи зменшити в одну й ту саму кількість разів?
33. Запишіть формулу обчислення середньої арифметичної способом моментів і поясніть її.
34. Що станеться з середньою, якщо всі частоти зменшити чи збільшити в однакову кількість разів?
35. Коли застосовують формулу середньої гармонічної?
36. Що слід розуміти під прямими й оберненими величинами в статистиці? Наведіть приклади прямих і обернених показників.
37. Коли застосовують просту середню гармонічну, а коли зважену?
38. Коли застосовують середню квадратичну?
39. За допомогою якої середньої можна визначити середні темпи динаміки та середні темпи приросту?
40. Запишіть формули середньої геометричної та продемонструйте вміння користуватися ними.
41. Як називається середня, обчислена з моментних абсолютних величин?
42. Як обчислити середнє значення моментного ряду динаміки з різними проміжками часу між датами?
43. Як обчислити середню прогресивну?
44. Як називається ознака, яка найчастіше зустрічається в сукупності?
45. Як визначити моду з інтервального ряду розподілу? Наведіть формулу й поясніть техніку обчислення.
46. Як називається ознака, що лежить посередині ранжованого ряду розподілу?
47. Як визначити медіану з інтервального ряду розподілу? Наведіть формулу й поясніть техніку обчислення.
Дата добавления: 2018-05-02; просмотров: 2446; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
