Оценка точности по коэффициенту ошибок
Для определения ошибки воспользуемся выражением для передаточной функции замкнутой системы по ошибке:
Разложим в ряд по возрастающей степени:
,
где С0, С1,…, Сn – коэффициенты ошибок.
При малых значениях 
этот ряд сходится. Коэффициенты ошибок могут быть найдены или по формуле Тейлора или путем деления многочлена числителя на знаменатель передаточной функции 
.
Если использовать формулу Тейлора:
Подставим выражение для в выражение для 
:
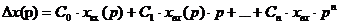
Сделаем обратное преобразование Лапласа:
Таким образом, получим, что статическая ошибка по входному воздействию будет определяться коэффициентом ошибок и характером изменения и величиной входного воздействия. Если хвх = const, то из этой формулы достаточно взять один первый член.
Если входное воздействие медленно изменяющаяся функция, то надо взять несколько первых членов.
Аналогично рассуждая можно показать, что ошибка по возмущающему воздействию xf(t) будет определяться:
Показатели качества САУ
Количественные оценки качества, так называемые прямые показатели качества, определяются по кривой переходного процесса.
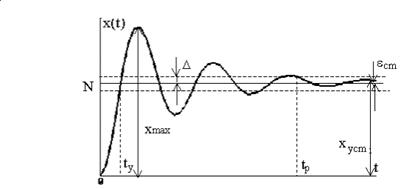
Рис. 7. Переходная функция и показатели качества
Используются следующие прямые показатели качества:
1) величина перерегулирования s,
которая характеризует максимальное отклонение регулируемой величины от ее установившегося значения, которое может быть определено в соответствии с теоремой о конечном значении оригинала
|
|
|
2) время переходного процесса или время регулирования tp – наименьшее значение времени, после которого имеет место неравенство
где D – заданная величина, обычно лежащая в пределах D=0.02–0.05;
3) статическая ошибка eсm – величина отклонения установившегося значения регулируемой величины x(¥) от требуемого значения N
или 
где E(s) – изображение ошибки;
4) время установления ty – промежуток времени, по истечении которого регулируемая величина первый раз достигает установившегося значения.
Для определения качества системы могут использоваться и другие показатели, соответствующие решаемой задаче, например, число колебаний регулируемой величины за время регулирования, частота и период колебаний и т.д.
Практическая часть
1. Нахождение АЧХ и ФЧХ для 
и 
, построение ЛАЧХ
Найдём АЧХ и ФЧХ для :
, где 
– оператор дифференцирования (Лапласа)
Заменим на 
и найдем комплексную АЧХ системы 
.
Обозначим 
-действительную часть передаточной функции 
, а 
-мнимую часть
, 
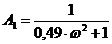Найдем амплитудно-частотную характеристику (АЧХ):
Найдем фазо-частотную характеристику (ФЧХ):
|
|
|
Найдем логарифмическую амплитудно-частотную характеристику (ЛАЧХ):
Построим найденные характеристики в математическом пакете MathCAD 2000:
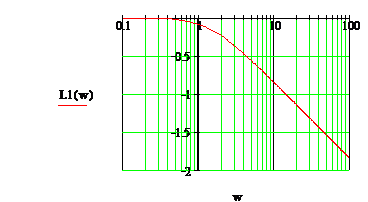
Рис. 8.ЛАЧХ звена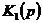 
Рис. 9 ЛФЧХ звена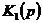
Из графика видно, что звено относится к инерционным звеньям и вносит запаздывание выходной величины от 
на низких частотах до 
высоких и имеет наклон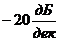 
.
Выполним те же действия для звена
Так как действительная часть передаточной функции равна 0, то
АЧХ запишется так:
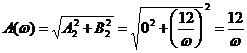
Найдем фазочастотную характеристику (ФЧХ):
Найдем логарифмическую амплитудно-частотную характеристику (ЛАЧХ):
Построим найденные характеристики:
Рис. 10. ЛАЧХ звена
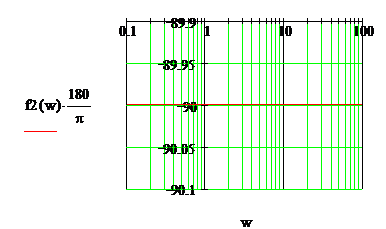
Рис. 14.ЛФЧХ звена
Как видно из графиков звено интегрирующее так как создает запаздывание выходной величины на всех частотах на 
, а наклон ЛАЧХ равен .
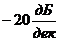2. Нахождение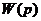 
, 
, 
, 
1) Найдем передаточную функцию разомкнутой системы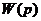
Рис. 11. Структурная схема передаточной функции разомкнутой системы
2) Найдем передаточную функцию замкнутой системы
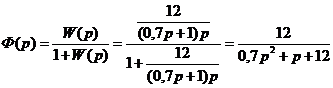
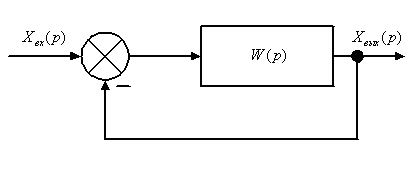
Рис. 12. Структурная схема передаточной функции замкнутой системы
3) Найдем передаточную функцию по ошибке
Также её называют передаточной функцией ошибки по задающему воздействию.
|
|
|
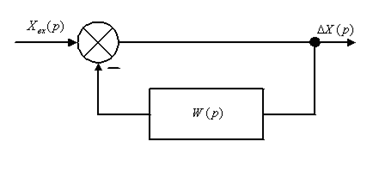
Рис. 13. Структурная схема передаточной функции по ошибке
4) Найдем передаточную функцию по внешнему воздействию
Рис. 14. Структурная схема передаточной функции внешнему воздействию
3. Нахождение АЧХ и ФЧХ для найденной , а так же построение ЛАЧХ и ФЧХ
Найдем АЧХ, ФЧХ и ЛАЧХ для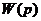
Найдем комплексную АЧХ системы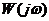 
, для этого заменим на
Обозначим А= 
, а В= 
Найдем амплитудно-частотную характеристику (АЧХ):
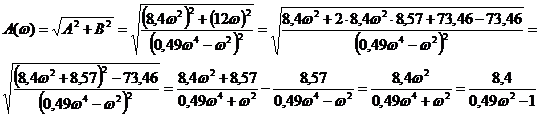
Найдем фазочастотную характеристику (ФЧХ):
Найдем логарифмическую амплитудно-частотную характеристику (ЛАЧХ):
Построим ЛАЧХ и ФЧХ для :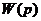
Рис. 15. АФЧХ звена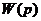
Рис. 16. ЛФЧХ звена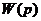
Исследование 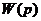на устойчивость по критериям Гурвица, Михайлова и Найквиста
Исследование 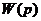по критерию Гурвица:
Сложим числитель и знаменатель передаточной функции 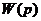приравняем полученное уравнение к нулю. Полученное уравнение называется характеристическим уравнением и запишется как
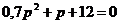
где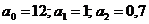 
Из уравнения видно, что все коэффициенты этого уравнения больше нуля.
Теперь составляем определитель 2-го порядка:
Составляем следующий определитель на ранг меньше предыдущего. Он определяется путем вычеркивания соответствующих строк и столбцов.
|
|
|
Т.к 
; 
и 
(все определители больше нуля), то данная система устойчива.
2) Исследование 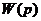на устойчивость по критерию Михайлова
Представим характеристическое уравнение 2-го порядка для данной передаточной функции в виде характеристического вектора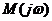 
. Данный вектор получается заменой оператора на . Уравнение данного вектора будет иметь вид:
где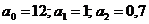
Пусть 
– действительная составляющая
– мнимая составляющая
Тогда 
где 
Для нашего уравнения получаем:
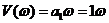
Таблица 1
|
|
|
| 0 | 12 | 0 |
| 1 | 11,3 | 1 |
| 2 | 9,2 | 2 |
| 4 | 0,8 | 4 |
| 5 | -5,5 | 5 |
| 10 | -58 | 10 |
Рис. 17. Изображение характеристического вектора
Из графика видно, что зависимость уходит в 
во 2-м квадранте. Полученный график подтвердил устойчивость системы по критерию Михайлова.
Исследование 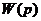на устойчивость по критерию Найквиста
Критерий Найквиста мы реализуем на комплексной плоскости. Если АЧХ разомкнутой системы не охватывает на комплексной плоскости точку с координатами (-1; j0), то система является устойчивой. Если АЧХ охватывает эту точку, то система – неустойчивая. Если проходит через эту точку, то система находится на границе устойчивости.
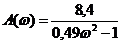
Таблица 2
|
| 
| 
|
| 0 | -8,4 | -1,57 |
| 0,5 | -9,57 | -1,23 |
| 1 | -16,47 | -0,96 |
| 5 | 0,47 | -0,27 |
| 10 | 0,175 | -0,14 |
По полученным данным построим диаграмму Найквиста
Рис. 18. диаграмма Найквиста
Как видно из построенного графика АЧХ разомкнутой системы на комплексной плоскости не охватывает точку с координатами (-1; j0). Следовательно можно сделать вывод, что система устойчивая. А расстояние от этой кривой до точки (-1; j0) есть запас устойчивости.
Вывод: Сравнив все три метода критерия устойчивости, можно судить о том, что данная система устойчива, так как все три метода показали одинаковый результат.
Дата добавления: 2018-05-02; просмотров: 565; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!