Абсолютная и относительная погрешности
Лабораторная работа №1.
Действия над приближенными числами
Цель работы: научится находить погрешности вычислений и округлять числа до значащего числа.
Результат действий над приближёнными числами представляет собой также приближённое число. Погрешность результата может быть выражена через погрешности первоначальных данных при помощи следующих теорем:
1. Предельная абсолютная погрешность алгебраической суммы равна сумме предельных абсолютных погрешностей слагаемых.
2. Относительная погрешность суммы заключена между наибольшей и наименьшей из относительных погрешностей слагаемых.
3. Относительная погрешность произведения или частного равна сумме относительных погрешностей сомножителей или, соответственно, делимого и делителя.
4. Относительная погрешность n-ой степени приближенного числа в n раз больше относительной погрешности основания (как у целых, так и для дробных n).
Пользуясь этими теоремами, можно определить погрешность результата любой комбинации арифметических действий над приближенными числами.
Примеры:
V = r2h
Dv = Vd v = V(2d r+d n)
Предельная абсолютная погрешность заведомо превосходит абсолютную величину истинной погрешности, поскольку предельное значение вычисляется в предположения, что различные погрешности усиливают друг друга; практически это бывает редко. При массовых вычислениях, когда не учитывают погрешность каждого отдельного результата, пользуются следующими правилами подсчета цифр.
|
|
|
При соблюдении этих правил можно считать, что в среднем полученные результаты будут иметь все знаки верными, хотя в отдельных случаях возможна ошибка в несколько единиц последнего знака.
1. При сложении и вычитании приближённых чисел в результате следует сохранять столько десятичных знаков, сколько их в приближённом данном с наименьшим числом десятичных знаков.
2. При умножении и делении в результате следует сохранять столько значащих цифр, сколько их имеет приближённое данное с наименьшим числом значащих цифр.
3. При возведении в квадрат или куб в результате следует сохранять столько значащих цифр, сколько их имеет возводимое в степень приближённое число ( последняя цифра квадрата и особенно куба при этом менее надежна, чем последняя цифра основания ).
4. При увеличении квадратного и кубического корней в результате следует брать столько значащих цифр, сколько их имеет приближённое значение подкоренного числа (последняя цифра квадратного и особенно кубического корня при этом более надёжна, чем последняя цифра подкоренного числа).
5. Во всех промежуточных результатах следует сохранять одной цифрой более, чем рекомендуют предыдущие правила. В окончательном результате эта запасная цифра отбрасывается.
|
|
|
6. Если некоторые данные имеют больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при умножении, делении, возведении в степень, извлечении корня), чем другие, то их предварительно следует округлить, сохраняя лишь одну лишнюю цифру.
Если данные можно брать с произвольной точностью, то для получения результата с K цифрами данные следует брать с таким числом цифр, какое даёт согласно правилам 1-4(К+1) цифру в результате.
Погрешности вычислений
При работе с приближенными величинами важно уметь:
1) давать математические характеристики точности приближенных величин;
2) зная степень точности исходных данных, оценить степень точности результатов и требуемую точность промежуточных вычислений;
3) правильно построить вычислительный процесс, чтобы избавить его от тех выкладок, которые не окажут влияния на точные цифры результата.
Источники погрешностей
Погрешность результата решения задачи складывается из трех составных частей:
– неустранимой погрешности решения, обусловленной неточностью исходных данных;
|
|
|
– погрешности метода решения задачи;
– вычислительной погрешности, являющейся результатом округлений в процессе счета.
Неустранимая погрешность решения обусловлена неточностью исходных данных, которые возникают в результате неточности измерений (инструментальная ошибка) или из-за невозможности представить необходимую величину конечным числом значащих цифр (ошибка округления). Инструментальная ошибка всегда возникает при проведении физического измерения, поскольку оно не может быть выполнено абсолютно точно. Ошибки округления при задании исходных данных возникают в том случае, когда величину невозможно представить ограниченным числом значащих цифр, например числа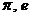 
и т.д.
Погрешности метода решения задач очень часто возникают при использовании численных методов. Действительно, многие математические задачи могут быть решены только приближенно, хотя и возможно со сколь угодно большой точностью, так как любой численный метод предполагает использование конечного числа арифметических операций. Например, при решении задачи обычно производную заменяют разностью, интеграл – суммой, или бесконечный итерационный процесс обрывают после некоторого конечного числа итераций. Так же к погрешностям метода можно отнести неточность отображения реальных процессов, так как рассматривается не сам процесс, а его идеализированная математическая модель.
|
|
|
При решении численных задач на компьютере всегда возникают вычислительные погрешности, обусловленные ошибками округления в процессе счета (так как вычисления на ЭВМ выполняются с конечным числом значащих цифр, определенных конечностью разрядной сетки ЭВМ). Исключения составляют задачи, в которых операции над данными выполняются точно, например в целочисленной арифметике. Однако в подавляющем большинстве вычислительных задач используются вещественные числа, операции над которыми выполняются с ошибками округления. В зависимости от реализованного в алгоритме метода решения, эти ошибки округления могут либо расти, либо уменьшаться. При расчетах те или иные погрешности могут отсутствовать или их влияние может быть мало.
Абсолютная и относительная погрешности
Абсолютная погрешность 
есть разница между истинным значением величины 
(считая это истинное значение известным) и ее приближенным значением 
.
Относительная погрешность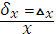 
определяется, как отношение абсолютной ошибки к приближенному значению величины. Казалось бы, что более естественно определить ее, как отношение абсолютной ошибки к точному значению, но обычно точное значение нам неизвестно. Все, что обычно бывает известно, - это приближенное значение величины и оценка ошибки или границы максимально возможной величины ошибки. Если ошибка мала, то разница в определениях не скажется на численной величине относительной ошибки.
Для величин, близких по значению к единице, абсолютная и относительная ошибки почти одинаковы. Для очень больших или очень малых величин относительная и абсолютная ошибки представляются совершенно разными числами.
Если из условия задачи или из контекста не ясно, какая ошибка имеется ввиду, то чаще считают, что ошибка относительная.
Дата добавления: 2018-04-15; просмотров: 404; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!