Кривые замораживания. Тепло, отводимое от сырья при замораживании
Кинетику процесс замораживания наилучшим образом характеризует так называемая температурная кривая замораживания (рис. 8). На кривой четко выделяются три основных этапа процесса:
I этап – процесс понижения температуры сырья (продукта) от любой начальной до криоскопической;
II этап – процесс кристаллообразования или перехода воды в составе тканей сырья 9продукта) из одного агрегатного состояния (жидкость) в другое – (кристаллы льда), этап представляет собой фазовый переход, сопровождается выделением скрытой теплоты фазового перехода – выделением скрытой теплоты кристаллизации воды ( 
кДж/кг); на данном этапе происходит резкое изменение ТФХ сырья 9продукта), в нем протекают глубокие физические, биохимические и микробиологические изменения;
III этап – процесс переохлаждения уже замороженного сырья (продукта) до требуемой температуры.
|
|
|
|
|
|
|
|
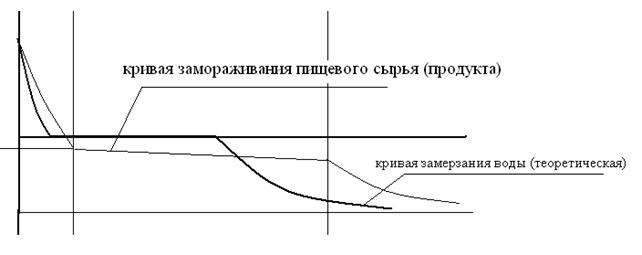
Рисунок 8 – Температурная кривая замораживания пищевого сырья
Тепло, отводимое от пищевого сырья (продукта) при замораживании, называется в холодильной технике расходом холода на замораживание. В соответствии с тремя основными этапами процесса замораживания, расход холода складывается из трех слагаемых.
В первый период происходит отвод тепла от сырья (продукта), при понижении его температуры от начальной до криоскопической. Это количество тепла может быть рассчитано по формуле
|
|
|
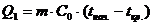, (59)
где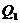 
- теплота, отводимая от сырья (продукта), кДж;
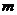- масса сырья (продукта), кг;
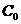- удельная теплоемкость сырья (продукта), кДж/(кг·К);
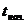- начальная температура сырья (продукта), ºС;
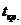- криоскопическая температура сырья (продукта), составляет минус 1 ºС.
На втором этапе замораживания имеет место фазовый переход – изменение агрегатного состояния воды в составе тканей сырья (продукта). Теплота, отводимая от продукта на этом этапе, может быть рассчитана по формуле
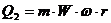, (60)
где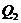 
- теплота, отводимая от сырья (продукта), кДж;
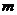- масса сырья (продукта), кг;
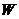- долевое содержание воды в сырье (продукте);
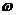- количество вымороженной воды (рассчитывается по формуле (37) или (38));
- скрытая теплота кристаллообразования, 334 кДж/кг.
На третьем этапе замораживания имеет место переохлаждение уже замороженного продукта до заданной (обоснованной ранее) температуры. Теплота, отводимая от продукта на этом этапе, может быть рассчитана по формуле
|
|
|
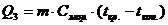, (61)
где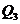 
- теплота, отводимая от сырья (продукта), кДж;
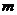- масса сырья (продукта), кг;
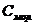- удельная теплоемкость замороженного сырья (продукта), кДж/(кг·К);
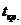- криоскопическая температура сырья (продукта), ºС;
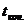- конечная температура сырья (продукта), ºС.
Тогда, суммарная теплота, отводимая от продукта при замораживании, или расход холода на замораживание составит
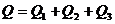. (62)
Вывод и анализ формулы Планка
Задача о продолжительности замораживания – одна из наиболее сложных в теплофизике замораживания, что обусловлено наличием большого числа влияющих на этот процесс факторов.
Каждый из существующих на сегодняшний день методов вычисления продолжительности замораживания специфически связан с исходной физической схемой процесса, его начальными и граничными условиям, которые задаются в частном виде, с допущениями, упрощающими задачу.
Физическая постановка задачи о продолжительности замораживания пищевых продуктов есть задача о теплопроводности в системах с подвижной границей раздела, под которой понимают перемещающуюся границу раздела между отвердевшей и жидкой фазами от периферии в глубь тела (сырья или продукта) по мере отвода теплоты от его поверхности.
|
|
|
Отвердевающую в таком процессе жидкость принято рассматривать как не подверженную свободному или вынужденному конвективному движению, если она распределена в виде мелких включений в пористом твердом теле или как-либо иначе, механически связана с неподвижной скелетной структурой тела, а также, если вязкость отвердевающей жидкости велика.
Классическим решением задачи о замораживании Международным институтом признано решение Р. Планка, полученное им в 1913 г. и существенно развитое им и другими исследователями в последующие годы. Формула для определения продолжительности замораживания называется по имени ее создателя – формула Планка, как фундаментальная, она включена в рекомендации Международного института холода.
Для упрощения задачи Планком было сделано несколько допущений, которые приведены ниже:
1. Теплоемкость замороженной части продукта равна нулю.
2. Тело перед началом замораживания охлаждено до криоскопической температуры.
3. Льдообразование в теле происходит без переохлаждения при криоскопической температуре; теплофизические свойства замороженной части (коэффициент теплопроводности и удельная теплоемкость) не зависят от температуры.
|
|
|
4. Тело однородно, его плотность при замораживании не меняется; коэффициент теплоотдачи и температура охлаждающей среды не зависят от времени.
Выведем формулу Планка для тела в форме пластины. Пусть за некоторый промежуток времени 
тело замерзло на толщину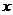 
(рис. 9). При этом выделилось тепло в количестве 
в результате превращения воды в лед. Тогда за промежуток времени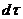 
, тело промерзнет на толщину 
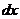, при этом выделится тепло в количестве 
.
|
|
|
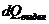Рисунок 9 – Вывод формулы Планка для тела в форме пластины
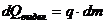, (63)
где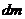 
- масса замороженного продукта, кг.
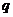- теплота, выделенная при замораживании единицы массы продукта, кДж/кг, рассчитывается по формуле
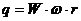, (64)
где 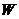- содержание воды в продукте, доли единицы;
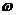- количество вымороженной воды, доли единицы;
- скрытая теплота льдообразования, кДж/кг.
Тогда, подставив выражение (64) в формулу (63) получим
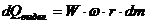. (65)
Если учесть, что масса продукта есть произведение его плотности на объем, то приращение массы замороженного продукта 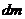составит
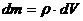, (66)
где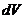 
- приращение замороженного объема продукта, м3.
Для пластины, площадь которой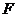 
, м2, а толщина 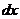, приращение объема составит
. (67)
Подставив выражения (67) и (66) в формулу (65) получим
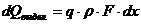. (68)
В силу третьего допущения Планка (теплоемкость замороженной части продукта равна нулю, что превращает коэффициент температуропроводности этой части продукта в бесконечность), вся теплота, которая выделилась в результате льдообрзования, будет передана через замороженный слой продукта 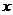к поверхности замораживаемого тела без потерь и должна быть отведена от нее охлаждающей средой 
.
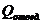Для отдностороннего замораживания тела через плоскую стенку (замороженный слой продукта) это количество теплоты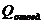 
может быть выражено уравнением теплопередачи через плоскую стенку
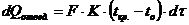, (69)
где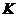 
- коэффициент теплопередачи, может быть рассчитан по формуле
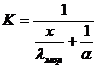, (70)
где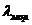 
- коэффициент теплопроводности мороженого продукта, Вт/(м·К);
- коэффициент теплоотдачи, Вт/(м2·К);
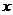- толщина стенки (толщина замороженного слоя продукта), м.
Так как
, (71)
то
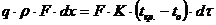, (72)
после преобразований, выразим из уравнения (72) 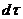, получим
. (73)
Уравнение (73) после интегрирования дает выражение для определения продолжительности замораживания тела в форме пластины – формулу Планка для пластины
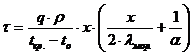. (74)
Очевидно, что при несоблюдении допущенных Планком упрощений, значительно усложнились бы условия интегрирования дифференциального уравнения (73).
В формуле (74) в случае одностороннего замораживания,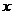 
- это полная толщина пластины, а в случае двустороннего замораживания 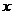- это половина толщины пластины.
Для тел в форме шара и цилиндра формула Планка получена аналогичным путем, имеет вид
- для цилиндра
, (75)
- для шара
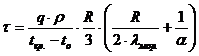, (76)
где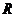 
- радиус шара, цилиндра, м.
Сравнив формулы (74), (75) и (76) можно сделать вывод, что минимальной продолжительность замораживания будет для тела в форме шара, а максимальной – для тела в форме пластины.
В силу сделанных Планком допущений, расчетные продолжительности замораживания будут отличаться от реальных примерно на 10-15 %, что вполне допустимо в инженерных расчетах.
Анализ формулы Планка позволяет выявить основные факторы, оказывающие влияние на продолжительность процесса замораживания, к ним относятся:
- коэффициент теплоотдачи охлаждающей среды, чем он больше, тем меньше продолжительность процесса замораживание и выше его скорость;
- температура охлаждающей среды, чем ниже температура охлаждающей среды, тем меньше продолжительность процесса и выше скорость замораживания;
- толщина продукта, причем зависимость носит квадратичный характер, то есть при увеличении толщины продукта, например, в 2 раза, продолжительность процесса возрастет в 4 раза.
Раздел 3: Научные основы консервирования пищевого сырья посолом
Лекция № 5: Научные основы консервирования пищевого сырья посолом. Классификация посола. Основы теории посола. Внешняя и внутренняя диффузия соли при посоле. Вывод уравнения продолжительности просаливания рыбы Рулева Н.Н.
Дата добавления: 2018-04-15; просмотров: 750; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!