Применения теории графов в различных сферах
Научной деятельности
Изучая элементы теории графов, многие студенты задаются вопросом: «А где же собственно я могу применять графы?». Я попытаюсь привести примеры использования элементов теории графов в различных научных сферах и жизненных ситуациях.
Графы нашли применение практически во всех отраслях научных знаний: математике, физике, биологии, химии, истории, лингвистике, технике и т.п.
Самое распространенное применение теории графов нашла в математике при решении логических задач и головоломок. Основой применения графов для решения логических задач служит выявление и последовательное исключение возможностей, заданных в условии. Возьмем, к примеру, такую задачу: «На пришкольном участке растут 8 деревьев: яблоня, тополь, береза, рябина, дуб, клен, лиственница и сосна. Рябина выше лиственницы, яблоня выше клена, дуб ниже березы, но выше сосны, сосна выше рябины, береза ниже тополя, а лиственница выше яблони. Расположите деревья от самого низкого к самому высокому».
Решение: Вершины графа – это деревья, обозначенный первой буквой названия дерева. Рассмотрим отношение дерево ниже чем другое и проведем стрелки о более низкого дерева к более высокому. Если в задаче сказано, что рябина выше лиственницы, то стрелку ставим от лиственницы к рябине и т.д. Получаем граф, на котором видно, что самое низкое дерево - клён, затем идут яблоня, лиственница, рябина, сосна, дуб, береза и тополь. (рис.5)
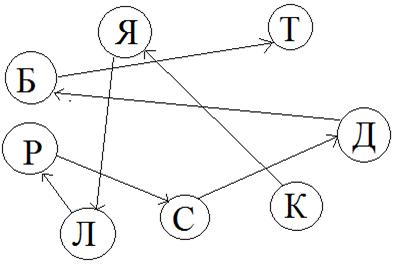
рис.5
Теория графов в медицине. Каждому человеку важно знать свою группу крови и резус-фактор. Всего существует четыре группы крови. При переливании крови от одного человека к другому не все группы совместимы. Оказывается, с помощью графа можно наглядно показать возможные варианты переливания крови. Группы крови – это вершины графа с соответствующими номерами, а стрелки указывают на возможность переливания одной группы крови человеку с другой группой крови. Например, кровь первой группы можно переливать любому человеку, а человек с первой группой крови воспринимает только кровь своей группы. (рис.6)
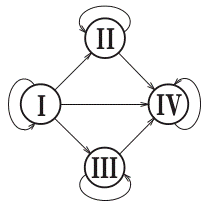
рис.6
Элементы теории графов используются и в экологии. Природные сообщества обладают сложным строением: несколькими уровнями, между которыми существуют разнообразные трофические (пищевые) и топические (не связные с цепью питания) связи. Структура трофической пирамиды может быть весьма различной, в зависимости от климата, почвы, ландшафта и других факторов.
При анализе биологических сообществ, принято строить пищевые или трофические сети, т.е. графы, вершины которых соответствуют видам, входящим в сообщество, а ребра указывают трофические связи между видами. Обычно такие графы – ориентированные: направление дуги между двумя вершинами указывает на тот из видов, который является потребителем другого, т.е. направление дуги совпадает с направлением потока вещества или биомассы в системе. Например трофическая сеть широколиственного леса. (рис.7)

рис.7
Теория графов нашла своё применение и в архитектуре и строительстве. При составлении больших проектов, содержащих различные виды работ часто возникает ситуация, когда ту или иную работу можно начать лишь по окончании других. Так при строительстве дома нельзя приступить к отделочным работам, пока не возведены стены, и нельзя возводить стены до укладки фундамента. Последовательность работ изображается в виде сетевых графиков.
Графы в физике и технике. Одной из самых сложных и утомительных задач радиотехники было конструирование печатных схем.
Печатная схема – пластинка из изолирующего материала, на которой в виде металлических полосок вытравлены дорожки. Пересекаться дорожки могут только в определенных точках, куда устанавливаются необходимые элементы (диоды, триоды, резисторы и другие), их пересечение в других местах вызовет замыкание электрической цепи. Решение этой задачи упростилось благодаря использованию теории графов. В ходе решения этой задачи необходимо вычертить плоский граф, с вершинами в указанных точках. А благодаря теории графов эта задача теперь формализована, и расчёт дорожек производит компьютер. (рис.8)

рис.8
Теория графов находит широкое применение в транспортных, коммуникационных системах. При строительстве новых кварталов, домов их принимают за вершины графа, а коммуникации – дороги, линии электропередачи, водопровод, тепловые сети – это рёбра и дуги.
Применение специальных методов на таком графе позволяет найти кратчайший удобный и оптимальный маршрут. При помощи графа производится поиск оптимальных путей прокладки коммуникаций. (рис. 9) В частности, графы широко применяются для маршрутизации данных в Интернете.

рис. 9
Помимо приведённых мной отраслей, в которых применяются графы, существует множество других.
Графы применяются в экономике и менеджменте, в информатике, в географии, в живописи, в психологии и рекламе. А также во многих других сферах нашей жизни.
Но всё-таки, существует ли такая область человеческих занятий, в которой теория графов, графы не играют никакой роли? Например, есть ли графы в искусстве, в музыке, поэзии?
Дата добавления: 2018-04-15; просмотров: 5166; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
