Основные понятия теории графов.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ»
Институт транспорта
Отделение СПО
Индивидуальный проект
По математике
“Теория графов”
Выполнил:
студент 1 курса
группы МГСт-16-9-1
Хорошилов Д. К.
Проверил:
преподаватель
Пискулина А. П.
г. Тюмень
2017
Оглавление.
Введение…………………………………………………………………………...3
1. Историческая справка……………………………………………………..5
2. Основные понятия теории графов………………………………………...7
3. Применения теории графов в различных
сферах научной деятельности…………………………………………….8
4. Применение графов в других областях………………………………….14
Заключение……………………………………………………………………….16
Список литературы………………………………………………………………17
Введение
Теория графов - это область дискретной математики, особенностью которой является геометрический подход к изучению объектов.
Первые задачи теории графов были связаны с решением математических развлекательных задач и головоломок. Одним из первых результатов в теории графов явился критерий существования обхода всех ребер графа без повторений, полученный Л. Эйлером при решении задачи о Кенигсбергских мостах.
Также с помощью графов можно упрощать условия задач по физике, химии, экологии и в других областях. Графы используют при составлении карт и генеалогических древ. Графами являются блок-схемы программ для ЭВМ, сетевые графики строительства, где вершины – события, означающие окончания работ на некотором участке, а ребра, связывающие эти вершины, - работы, которые возможно начать по совершении одного события и необходимо выполнить для совершения следующего. Одними из самых распространённых графов являются схемы линий метрополитена.
|
|
|
Цель: с помощью графов научиться быстро решать практические задачи.
Гипотеза исследования: метод графов очень важен и широко применяется в различных областях науки и жизнедеятельности человека.
Задачи исследования:
· Изучить информацию по теории графов;
· Исследовать практические навыки в применении элементов теории графов;
· Найти применение теории графов в различных областях науки и техники.
Актуальность и новизна:
Теория графов позволяет решать наиболее легким способом, наглядно многие логические задачи, которые способствуют развитию мышления и интеллекта.
Сейчас почти в любой отрасли науки и техники встречается применение графов.
· в физике - при построении электрических схем,
|
|
|
· в химии и биологии - при изучении молекул и их цепочек,
· в географии – при составлении карт,
· в истории – при составлении родословной,
· в геометрии – в чертежах многоугольников, многогранников, пространственных фигур,
· в экономике – при решении задач о выборе оптимального пути для потоков грузового транспорта (схем авиалиний, метро, железных дорог).
· и в других областях
Историческая справка.
Историю возникновения этой теории можно проследить по переписке великого ученого Л.Эйлера. В ней он сообщал, что ему была предложена задача о семи мостах Кенигсберга. Спрашивалось, может ли кто-нибудь непрерывно обойти их, проходя только однажды через каждый мост. И ему сразу же было сообщено, что никто еще до сих пор не мог это проделать, но никто и не доказал, что это невозможно. Вопрос этот показался ему достойным внимания тем, что «…Для его решения недостаточны ни геометрия, ни алгебра, ни комбинаторное искусство...». После долгих размышлений он нашел легкое правило, основанное на вполне убедительном доказательстве, с помощью которого можно во всех задачах такого рода определить, может ли быть совершен такой обход через какое угодно число и как угодно расположенных мостов или не может. Кенигсбергские же мосты расположены так, что их можно представить на рисунке (рис.1), на котором А обозначает остров, а В, С и D - части континента, отделенные друг от друга рукавами реки. Семь мостов обозначены буквами а, b, с, d, е, f, g.
|
|
|

рис. 1
Математик писал, что переход возможен, если на участке разветвления реки имеется не более двух областей, в которые ведет нечетное число мостов.
Для того чтобы проще представить себе это, будем стирать на рисунке уже пройденные мосты. Легко проверить, что если начать двигаться в соответствии с правилами Эйлера, пересечь один мост и стереть его, то на рисунке будет изображен участок, где опять имеется не более двух областей, в которые ведет нечетное число мостов. А при наличии областей с нечетным числом мостов мы будем располагаться в одной из них. Продолжая двигаться так далее, пройдем через все мосты по одному разу.
В ходе рассуждений Эйлер пришёл к следующим выводам:
· Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно.
· Не может существовать граф, который имел бы нечётное число нечётных вершин.
· Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
|
|
|
· Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
Граф кёнигсбергских мостов имел четыре нечётные вершины (т. е. все), следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.
Основные понятия теории графов.
В математике определение графа дается так:
Графом называется конечное множество точек, некоторые из которых соединены линиями. Точки называются вершинами графа, а соединяющие линии – рёбрами.
Граф состоит из вершин, связанных линиями. Если линия направленная (со стрелкой), то она называется дугой; линия ненаправленная (без стрелки) называется ребром. Линия, выходящая из некоторой вершины и входящая в нее же, называется петлей.
Количество рёбер, выходящих из вершины графа, называется степенью вершины. Вершина графа, имеющая нечётную степень, называется нечетной, а чётную степень – чётной.
Схема графа, состоящая из «изолированных» вершин, называется нулевым графом.(рис.2)
Графы, в которых не построены все возможные ребра, называютсянеполными графами. (рис.3)
Графы, в которых построены все возможные ребра, называются полными графами. (рис.4)

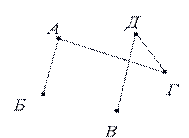
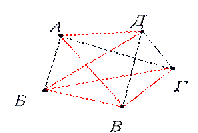
рис. 2 рис. 3 рис. 4
Дата добавления: 2018-04-15; просмотров: 966; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
