А.3 Приклади визначення нечітких відношень
Приклад 8. Нехай X = {x1, x2, x3}, Y = {y1, y2, y3, y4}, M = [0, 1]. Нечітке відношення R = X R Y може бути задане таблицею:
| R | y1 | y2 | y3 | y4 |
| x1 | 0 | 0 | 0.1 | 0.3 |
| x2 | 0 | 0.8 | 1 | 0.7 |
| x3 | 1 | 0.5 | 0.6 | 1 |
Приклад 9. Нехай X = Y = (-∞,∞), тобто множина усіх дійсних чисел. Відношення x » у (х забагато більший ніж y) можна задати функцією приналежності:
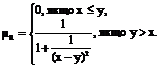
Приклад 10. Відношення R, для котрого  при достатньо великих k можна інтерпретувати так: «х та у близькі одне до одного числа».
при достатньо великих k можна інтерпретувати так: «х та у близькі одне до одного числа».
Приклад 11. Нехай нечіткі відношення R1 та R2 задаються таким таблицями:
| R1 | y1 | y2 | y3 |
| x1 | 0.1 | 0.7 | 0.4 |
| x2 | 1 | 0.5 | 0 |
| R2 | z1 | z2 | z3 | z4 |
| y1 | 0.9 | 0 | 1 | 0.2 |
| y2 | 0.3 | 0.6 | 0 | 0.9 |
| y3 | 0.1 | 1 | 0 | 0.5 |
Тоді нечітке відношення R1•R2 може бути задане таблицею:
| R1•R2 | z1 | z2 | z3 | z4 |
| x1 | 0.3 | 0.6 | 0.1 | 0.7 |
| x2 | 0.9 | 0.5 | 1 | 0.5 |
При цьому:
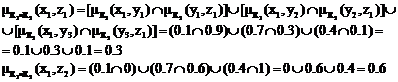
У цьому прикладі спочатку використаний «аналітичний» спосіб композиції відносин R1 і R2, тобто i-й рядок R1 «збільшується» на j-й стовпець R2 з використанням операції 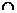 , потім отриманий результат «згортається» з використанням операції
, потім отриманий результат «згортається» з використанням операції 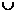 в µ(xi, zj).
в µ(xi, zj).
А.4 Приклад дефазифікації
Приклад 12. Нехай ми маємо нечітку множину для поняття "чоловік середнього росту": A={0|155, 0,1|160, 0,3|165, 0,8|170, 1|175, 1|180, 0,5|185, 0|190}. Необхідно провести дефазифікацію нечіткої множини "чоловік середнього росту" за методом центра тяжіння.
Застосуємо формулу:
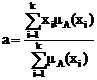 ,
,
де k - кількість елементів у множині A, та отримаємо: ·
|
|
|
a = (0·155 + 0,1·160 + 0,3·165 + 0,8·170 + 1·175 + 1·180 + 0,5·185 +
+ 0·190) / (0 + 0,1 + 0,3 + 0,8 + 1 + 1 + 0,5 + 0) = 175,4.
А.5 Приклад спадного нечіткого виведення
Приклад 13. Спадне нечітке логічне виведення. Нехай задана модель діагностики системи, що складається з двох передумов і трьох висновків: X={x1, х2}, Y = {у1, у2, у3}, а, матриця нечітких відносин має вигляд:
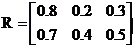 .
.
Допустимо в результаті діагностики системи були отримані наступні висновки: Y = 0.8/у1 + 0.2/у2 + 0.3/у3.
Необхідно знайти передумови, що до цього призвели: А = а1/х1-а2/х2.
З урахуванням конкретних даних відносини між передумовами і висновками будуть представлені в такий спосіб:
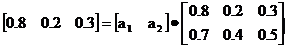
або в транспонованому вигляді:
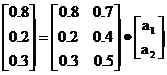
При використанні max-min-композиції останнє співвідношення перетвориться до вигляду:
0.8 = (0.8 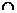 а1)
а1) 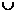 (0.7
(0.7 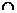 а2),
а2),
0.2 = (0.2 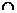 а1)
а1) 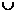 (0.4
(0.4 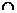 а2),
а2),
0.3 = (0.3 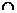 а1)
а1) 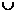 (0.5
(0.5 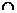 а2).
а2).
При вирішенні даної системи помітимо, що в першому рівнянні другий член правої частини не впливає на ліву частину: 0.8 = 0.8 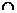 а1, а1 ≥ 0.8.
а1, а1 ≥ 0.8.
З другого рівняння одержимо: 0.2 = 0.4 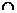 а2, а2 ≤ 0.2.
а2, а2 ≤ 0.2.
Отримане рішення задовольняє третьому рівнянню. У такий спосіб: 0.8<а1<1, 0<a2<0.2.
При рішенні практичних задач можуть одночасно використовуватися різні правила композиції нечітких виведень. Сама схема виведень може бути багатокаскадною. В даний час загальних методів рішення подібних задач, очевидно, не існує.
|
|
|
A.6 Приклади роботи із функціями пакета MATLAB
Приклад 14. Створити на мові пакету MATLAB m-функцію, що реалізує колоколообразну функцію приналежності
 .
.
function mu=bellmf(x, params)
%bellmf - колоколообразна функцiя приналежностi;
%x – вхiдний вектор;
%params(1) – коефіцієнт концентрацiї (>0);
%params(2) – координата максимуму.
a=params(1);
b=params(2);
mu=1./(1 + ((x - b)/a).^2);
Приклад 15. Використання функції fuzarith.
% визначення розподіляючої здатності функцій приналежності
point_n = 101;
min_x = -20; max_x = 20;% унiверсальна множина є [min_x, max_x]
x = linspace(min_x, max_x, point_n)';
A = trapmf(x, [-10 -2 1 3]);% трапецiєдальна нечiтка множина A
B = gaussmf(x, [2 5]);% гаусiвська нечiтка множина B
C1 = fuzarith(x, A, B, 'sum');
subplot(2,2,1);
plot(x, A, 'y--', x, B, 'm:', x, C1, 'c');
title('нечiтке додавання A+B');
C2 = fuzarith(x, A, B, 'sub');
subplot(2,2,2);
plot(x, A, 'y--', x, B, 'm:', x, C2, 'c');
title('нечiтке вирахування A-B');
C3 = fuzarith(x, A, B, 'prod');
subplot(2,2,3);
plot(x, A, 'y--', x, B, 'm:', x, C3, 'c');
title('нечiтке множення A*B');
C4 = fuzarith(x, A, B, 'div');
subplot(2,2,4);
plot(x, A, 'y--', x, B, 'm:', x, C4, 'c');
title('нечiтке дiлення A/B');
Зауваження. У програмах на мові MATLAB небажано використовувати кириличні літери. У наведених прикладах україномовні фрази наведено лише для пояснення тексту програм.
|
|
|
Приклад 16. Використання функцій створення нейро-нечітких мереж. Апроксимувати залежність:
 , xÎ[0, 10], Dx=0,1.
, xÎ[0, 10], Dx=0,1.
x = (0:0.1:10)'; % задаємо масив х
y = sin(2*x)./exp(x/5); % визначаємо значення елементів масиву y
trnData = [x y]; % створюємо масив навчаючої вибірки
numMFs = 5; % кількість функцій приналежності
mfType = 'gbellmf'; % тип функцій приналежності
epoch_n = 20;% кількість ітерацій
% створюємо FIS-структуру типу Сугено
in_fismat = genfis1(trnData,numMFs,mfType);
% навчаємо FIS-структуру
out_fismat = anfis(trnData,in_fismat,20);
% будуємо графіки:
% цільової залежності - синій колір, суцільна лінія
% апроксимуючої залежності - зелений колір, пунктир
plot(x,y,x,evalfis(x,out_fismat));
% підписуємо легенду до графіків
% Training Data - навчальна вибірка - цільові дані
% ANFIS Output - вихід ANFIS - розрахункові дані
legend('Training Data','ANFIS Output');
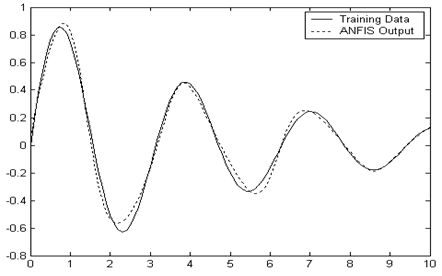 |
Рисунок А.2 - Графіки цільової та апроксимуючої залежностей
Дата добавления: 2018-04-15; просмотров: 419; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
