Подведение под знак дифференциала.
Томский государственный университет систем управления и радиоэлектроники
Приходовский М.А.
Математика - 2 семестр
Курс лекций
Учебное пособие
Для специальностей
Прикладная информатика в экономике»
Информатика и вычислительная техника»
Томск
ТУСУР
2018
Настоящее электронное учебное пособие составлено и скорректировано с учётом реального проведения лекций на ФСУ (профилирующая кафедра АСУ) группах 447-1,2 и 437-1,2,3 весной 2018 года.
Доказательства, которые попадают в билеты, выделены и в тексте обозначением (ДОК1), а в приложении указано, в какой лекции их искать (Л1).
Оглавление по темам
| ГЛАВА 1. ИНТЕГРАЛЫ. §1. Определения и основные методы. §2. Интегрирование рациональных дробей. §3. Интегрирование иррациональностей. §4. Интегрирование тригонометрических функций. §5. Интегралы, в которых проявляется взаимосвязь иррациональностей и тригонометрических функций . §6. Определённый интеграл и его приложения. §7. Несобственный интеграл. §8. Кратные интегралы. Приложение (список теор. вопросов)..................................... Литература.................................................................................. | 5 5 13 18 20 25 28 39 47 |
Оглавление по номерам лекций
| Лекция № 1. 14.02.2018................................................. Лекция № 2. 21.02.2018................................................. Лекция № 3. 28.02.2018................................................. Лекция № 4. 07.03.2018................................................ Лекция № 5. 14.03.2018................................................. Лекция № 6. 21.03.2018................................................. Лекция № 7. 28.03.2018................................................. Лекция № 8. 04.04.2018................................................ Лекция № 9. 11.04.2018................................................ Лекция № 10. 18.04.2018............................................... Лекция № 11. 25.04.2018............................................... Лекция № 12. 02.05.2018............................................... Лекция № 13. 16.05.2018............................................... Лекция № 14. 23.05.2018............................................... Лекция № 15. 30.05.2018............................................... Приложение (список теор. вопросов)............................ Литература ..................................................................... | 5 17 28 38 47 |
|
|
|
ЛЕКЦИЯ № 1. 14.02.2018
ГЛАВА 1. ИНТЕГРАЛЫ.
Определения и основные методы.
Определение. Если 
, то 
называется первообразной от функции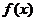 
.
Свойство 1.Если первообразная, то 
(для любого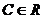 
) тоже является первообразной для той же самой функции .
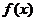Это легко доказать, действительно, 
= 
= .
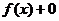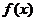Таким образом, первообразных бесконечно много, то есть, если поднять или опустить на любую высоту график , снова будет первообразная.
|
|
|
Свойство 2.Если 
и 
две различные первообразные функции 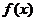, то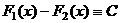 
.
Доказывается так: 
, т.е.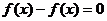 
.
Определение. Множество всех первообразных от одной и той же функции 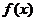называется неопределённым интегралом этой функции. Обозначение: 
.
Свойства линейности.
1. 
2. 
Замечание.
Для произведения свойство 
не существует. Чтобы убедиться в этом, достаточно рассмотреть любые 2 простейшие функции, например 
, 
. Тогда:
= 
= 
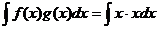, в то же время
= 
= 
.
Впрочем, можно даже рассмотреть 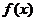произвольную, 
. Тогда 
,
= 
.
Таблица основных интегралов.
( 
)
; 
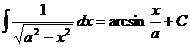
Объяснение причины возникновения модуля в 
. Функция 
существует только на правой полуоси, тогда как 
имеет две ветви, на правой и левой полуоси. Получалось бы противоречие, что производная от несуществующей функции есть на левой полуоси. Функция 
является чётным продолжением на левую полуось, и именно она там является первообразной для при 
.
Методы интегрирования.
Преобразования подынтегральных выражений.
Различные преобразования, например, арифметические (домножить и поделить, прибавить и отнять), выделение полного квадрата, разбиение многочлена на множители, преобразования по тригонометрическим формулам, и т.д. нередко помогают упростить исходное выражение, разбить его на несколько более простых слагаемых, которые уже сводятся к интегралам табличного типа. На практике рассмотрены разнообразные примеры на виды этих преобразований. Часто нужно домножить и поделить, чтобы сформировать готовое выражение, являющееся производной от известной функции. Например,
|
|
|
Пример. = 
= .
Когда сформировали выражение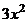 
, а заодно поделили на 3 перед интегралом, теперь уже точно невозможно перепутать или забыть коэффициент.
Аналогично, допустим, что мы помним, что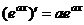 
. Тогда можно постараться сформировать готовое выражение типа 
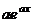внутри интеграла. Тем самым мы автоматически докажем, что при интегрировании такое выражение на этот коэффициент делится, а не домножается:
Пример. 
= 
= 
.
Тригонометрические преобразования:
Пример. Вычислить 
.
Решение. Применим формулу понижения степени.
= 
= 
=
= 
.
Пример. Вычислить 
.
Решение. = 
= 
=
= 
.
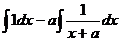Ответ. .
Замена переменной.
Бывают такие случаи, когда функция имеет вид 
, то есть явно видно, что всё выражение зависит от какого-то однотипного блока, например всё выражается через 
или 
. Делается замена на 
, только нужно не забыть пересчитать 
, потому что 
, если только замена не является простым линейным сдвигом 
.
|
|
|
Пример. Вычислить 
.
Решение. Сделаем замену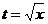 
, тогда 
, 
, 
.
= 
= 
= 
.
Обратная замена: = 
= 
.
Более того, область определения исходной функции 
из-за наличия в ней квадратного корня, точка 0 не входит в область определения, так как корень там и в знаменателе, так что знак модуля в ответе является излишним, ответ можно записать так: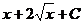 
.
Если в функции присутствуют корни разного порядка, например и 
, то замена должна происходить через корень порядка НОК (наименьшее общее кратное). Причина в том, что именно при этом все корни переводятся в целые степени от .
Если 
, тогда: 
, 
.
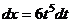Объяснение, почему все корни выразятся через целые степени :
= 
,
= 
.
Подведение под знак дифференциала.
Если интеграл имеет вид 
, то есть в функции присутствует какой-то множитель, который достаточно легко подлежит интегрированию, а в остальном множителе есть явная зависимость от его первообразной, то это значит, что подынтегральная функция есть производная от композиции . Тогда можно 
объединить и назвать 
, и далее 
можно будет повсеместно заменить на . Рассмотрим, как это действует, на примерах.
Пример. Вычислить 
.
Решение. = 
, фактически здесь уже подготовлена замена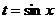 
, более того, дифференциал пересчитывать не нужно, потому что под дифференциалом и так сформировано то же самое, что будет называться . То есть, это частный случай замены переменных, только более простой.
Итак, вид интеграла получается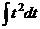 
= 
.
Сделаем обратную замену, и вот ответ: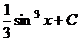 
.
Проверка: 
= 
= 
, то есть именно исходную подынтегральную функцию мы и получили.
Интегрирование по частям.
Существует более общий метод, чем подведение под знак дифференциала. Иногда вовсе не требуется, чтобы первообразная от того множителя, который подводится под dx, была как-то связана с остальной частью функции. Запишите формулу:
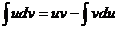
Такой короткий вид легче выучить наизусть, а теперь запишем более подробно, чтобы понять смысл.
.
Если есть два множителя, и один из них интегрируется довольно легко (он обозначен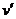 
) то можно перейти к интегралу, в котором наоборот, 
понижено до производной, а 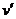повышено до первообразной. Иногда именно это помогает упростить дальнейшие вычисления.
Дата добавления: 2018-04-15; просмотров: 358; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!