Повторение испытаний. Формула Бернулли.
Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.
Вероятность появления события в каждом испытании постоянна и равна р. Следовательно, вероятность непоявления события в каждом испытании также постоянна и равна q=1-p (как вероятность противоположного события).
Формула Бернулли определяет вероятность появления ровно k раз события А в серии из n независимых испытаний, в каждом из которых вероятность появления события А равна р:
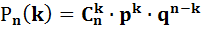
Вероятность того, что в n испытаниях событие наступит:
а) менее k раз
(0≤ 
<k) = 
(0)+ (1)+ (2)+ 
(k-1);
б) более k раз
(k< ≤n) = (k+1)+ (k+2)+ (k+3)+ (n);
в) не менее k раз
(k≤ ≤n) = (k)+ (k+1)+ (k+2)+ (n);
г) не более k раз
(0≤ ≤k) = (0)+ (1)+ (2)+ (k);
Пример 7. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три партии из шести (ничья во внимания не принимается)?
Решение. Играют равносильные шахматисты, поэтому вероятность выигрыша р = 
; следовательно, вероятность проигрыша q также равна . Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выиграны партии, то применима формула Бернулли.
Найдем вероятность того, что две партии из четырех будут выиграны:
= 
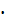
=0,375; ( 
)
Найдем вероятность того, что три партии из четырех будут выиграны:
|
|
|
= 
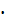
=0,3125; ( 
)
Так как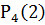 
> 
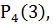то вероятнее выиграть две партии из четырех.
Лекция №3. Случайные величины и их числовые характеристики.
1.Закон распределения дискретной случайной величины.
2. Числовые характеристики ДСВ и их свойства.
3. Непрерывные случайные величины.
Закон распределения дискретной случайной величины
Под случайной величиной понимается переменная, которая в результате испытания в зависимости от случая принимает одно из возможных значений (какое именно - заранее не известно).
Примеры случайных величин: число произведенных выстрелов до первого попадания; дальность полета артиллерийского снаряда и т. п.
Случайная величина называется дискретной (прерывной), если она принимает отдельные, изолированные возможные значения с определенными вероятностями.
Число возможных значений ДСВ может быть конечным и бесконечным.
Под непрерывной случайной величиной будем понимать величину, бесконечное множество значений которой есть некоторый интервал (конечный или бесконечный) числовой оси.
Случайные величины будем обозначать прописными буквами латинского алфавита X, Y,Z,…,а их значения – соответствующими строчными буквами x, y, z,….
|
|
|
Наиболее полным, исчерпывающим описанием случайной величины является ее закон распределения.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Закон распределения случайной величины можно задать таблично, графически, аналитически.
При табличной форме задания закона распределения случайной величины, первая строка таблицы содержит возможные значения, а вторая – их вероятности.
| X | 
| 
| 
| … | 
|
| P | 
| 
| 
| … | 
|
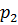
Причем 
=1
Для графического изображения закона распределения случайной величины в прямоугольной системе координат строят точки с координатами ( 
, 
а затем соединить их отрезками прямых. Полученную фигуру называют многоугольником распределения.
Пример
Задан закон распределения дискретной случайной величины:
| Х | 1 | 3 | 6 | 8 |
| Р | 0,2 | 0,1 | 0,4 | 0,3 |
Построить многоугольник распределения.
Решение.
В прямоугольной системе координат построим точки с координатами (1;0,2), (3;0,4), (6;0,4), (8;0,3), а затем соединим их отрезками прямых.
Получим:
Дискретную случайную величину Х- число появления события в n независимых испытаниях, в каждом из которых вероятность появления события равна p(0<р<1) называют подчиненной биномиальному закону распределения. Вероятность возможного значения Х=k (числа k появлений события) вычисляется по формуле Бернулли:
|
|
|
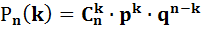
Если число n испытаний велико, а вероятность р появления события в каждом испытании очень мала, то используют приближенную формулу:
= 
,
где k- число появления события в n независимых испытаниях, 
np (среднее число появления события в n независимых испытаниях), и говорят , что случайная величина распределена по закону Пуассона.
Дата добавления: 2018-04-15; просмотров: 645; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!