ОПРЕДЕЛЕНИЕ ДИРЕКЦИОННЫХ УГЛОВ ГИРОСТОРОН

 

Принципиальная схема определения дирекционного угла гироскопическим способом приведена на рис. 10.

Дирекционный уголь гиростороны подземной маркшейдерской сети определяют по формуле

a = A - g = G + d - g ,                                                 (27)

где А - астрономический азимут стороны; g - плоское сближение меридианов в точке установки гирокомпаса; Г - гироскопический азимут стороны; d - поправка гирокомпаса.

 

Рис. 10. Схема определения дирекционного угла гироскопическим способом.

BD - исходная сторона на земной поверхности; EF - ориентируемая сторона подземной маркшейдерской опорной сети; С - направление меридианов, проходящих через точки В и Е; С_r - "гирокомпасный" меридиан.

Если гирокомпас используют для работы в пределах только одной шахты или поправку гирокомпаса определяют на каждой шахте, то дирекционный уголь гиростороны находят по формуле

a = G + d_м + d_g ,                                                     (28)

где d_м - местная поправка гирокомпаса; d_g - разность плоских сближений меридианов в точках установки гирокомпаса на земной поверхности и в горных выработках.

Гироскопический азимут стороны вычисляют по формуле

Г = (N - N_o) + e ,                                              (29)

где N - отсчет по лимбу угломерной части гирокомпаса, соответствующий примычному направлению на один из пунктов исходной или ориентируемой стороны; N_о - отсчет по лимбу угломерной части гирокомпаса, соответствующий положению равновесия ЧЭ (место нуля гирокомпаса); e - поправка за закручивание подвеса.

Место нуля гирокомпаса определяют из наблюдения четырех последовательных точек реверсии прецессионных колебаний ЧЭ и вычисляют по формулам

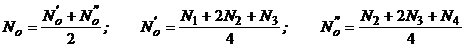 ,          (30)

где  - промежуточные средние; N₁, N₂, N₃, N₄ - отсчеты по лимбу угломерной части гирокомпаса, соответствующие точкам реверсии ЧЭ.

При пропуске второй, третьей или четвертой точек реверсии по техническим причинам достаточно провести наблюдение дополнительной пятой точки реверсии. При этом место нуля гирокомпаса определяют по соответствующим формулам:

          

                        (31)

           

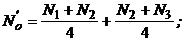
Поправку e за закручивание подвеса гирокомпаса определяют по формуле e = y/D, где D - добротность гирокомпаса, y - угол закручивания подвеса.

Добротность гирокомпаса D выражается отношением максимального направляющего момента гирокомпаса на данной широте к удельному моменту кручения подвеса (при закру­чивании на угол, равный радиану) и определяется в соответствии с указаниями руководства по эксплуатации прибора.

Угол закручивания подвеса y состоит из двух углов y = y_к + y_т, где y_к - угол закручивания подвеса, возникающий из-за неточного ориентирования корпуса гироблока; y_т, - угол закручивания подвеса, возникающий из-за изменения нулевого положения подвеса.

Величины y_к и y_т определяют по формулам

y_к = N_к -N_o;                                                        (32)

y_т = (n_o - n_к)t,

где N_к - отсчет по лимбу гирокомпаса, соответствующий положению визирной оси зритель­ной трубы, при которой средний штрих шкалы в поле зрения автоколлимационной трубы совмещен с неподвижным биссектором; n_к - отсчет по шкале автоколлимационной трубы, соответствующей положению неподвижного биссектора при определении нуля подвеса; n_o - место нуля подвеса; t - цена деления шкалы в поле зрения автоколлимационной трубы (в угловой мере).

Положение равновесия свободных колебаний ЧЭ (с невращающимся ротором) называют местом нуля подвеса, определяют из наблюдений четырех последовательных точек реверсии ЧЭ, характеризуют соответствующим отсчетом n_o по шкале автоколлимационной трубы и рассчитывают по формуле

 ,                                                   (33)

где n^'_o и n^"_o - промежуточные средние, вычисляемые по формулам

                              (34)

где n₁, n₂, n₃, n₄ - отсчеты по шкале автоколлимационной трубы, соответствующие точкам реверсии ЧЭ.

Местную поправку гирокомпаса вычисляют по формуле

d_м = a_о - Г_о,                                                        (35)

где a_о - дирекционный угол исходной стороны; Г_о - гироскопический азимут исходной стороны.

В случае, когда контрольное значение местной поправки гирокомпаса d_му определяли в точке с ординатой у, а предшествующие - в точке с ординатой у_о, полученное значение поправки следует исправить поправкой d_g за разность сближений меридианов.

Приведенное к точке с ординатой У значение местной поправки вычисляют по формуле

d_муо = d_му - d_g.                                                      (36)

Поправку за разность сближений меридианов d_g вычисляют для каждой ориенти­руемой стороны подземной сети по формуле

d_g = d_gу +d_gх,                                                        (37)

где d_gу = m_о(у_о -у); d_gх = у(m_о -m); m_о = 32.23tgB_o; m = 32.23tgB; d_g - поправка, с; у_о и В_о - ордината (км) и широта точки установки гирокомпаса на земной поверхности при определении поправки гирокомпаса; у и В - ордината (км) и широта точки установки гирокомпаса при определении гироскопического азимута ориентируемой стороны в шахте или на земной поверхности при контрольном измерении поправки.

Ординаты определяют до десятых долей километра. Коэффициент m выбирают из табл. 23 по абсциссе или широте точки установки.

Поправку гирокомпаса можно определять двумя путями: 1) независимо дважды - перед началом работ по ориентированию и после их окончания; 2) из 5-6 последних определений поправки, включая и контрольные.

Первый способ определения поправки применяют главным образом при неустой­чивой поправке и после длительной транспортировки прибора на объект. За окончательный результат принимают среднее из определений.

Второй способ определения поправки применяют, как правило, при сравнительно большом объеме разовых работ на одном объекте. Поправку определяют методом сколь­зящего среднего - как среднее арифметическое из 5-6 определений, включая контрольные, часть из которых непосредственно предшествовала ориентированию стороны, а другая часть получена после ее ориентирования.

Пример вычисления поправки гирокомпаса по 5 измерениям приведен в табл. 24.

Таблица 23

Значения коэффициента m для вычисления разности d_g плоских сближений меридианов

 

х,	m,	В		х,	m,	В		х,	m,	В
км	с/км	°	¢	км	с/км	°	¢	км	с/км	°	¢
3800	22,00	34	19	5800	41,73	52	19	6900	61,14	62	12
850	22,38	34	46	850	42,42	52	46	925	61,70	62	25
900	22,75	35	13	900	43,11	53	13	950	62,32	62	39
950	23,13	35	40	950	43,83	53	40	975	62,90	62	52
4000	23,53	36	07	6000	44,56	54	07	7000	63,54	63	06
050	23,91	36	34	025	44,94	54	21	025	64,14	63	19
100	24,30	37	01	050	45,30	54	34	050	64,79	63	33
150	24,70	37	28	075	45,69	54	48	075	65,41	63	46
200	25,11	37	55	100	46,06	55	01	100	66,09	64	00
250	25,52	38	22	125	46,47	55	15	125	66,73	64	13
300	25,93	38	49	150	46,84	55	28	150	67,43	64	27
350	26,35	39	16	175	47,22	55	41	175	68,09	64	40
400	26,78	39	43	200	47,64	55	55	200	68,81	64	54
450	27,21	40	10	225	48,03	56	08	225	69,50	65	07
500	27,64	40	37	250	48,45	56	22	250	70,19	65	20
550	28,09	41	04	275	48,85	56	35	275	70,95	65	34
600	28,53	41	31	300	49,29	56	49	300	71,67	65	47
650	28,99	41	58	325	49,70	57	02	325	72,46	66	01
700	29,45	42	25	350	50,15	57	16	350	73,20	66	14
750	29,92	42	52	375	50,56	57	29	375	74,02	66	28
800	30,39	43	19	400	51,02	57	43	400	74,79	66	41
850	30,88	43	46	425	51,45	57	56	425	75,63	66	55
4900	31,36	44	13	6450	51,92	58	10	7450	76,43	67	08
4950	31,86	44	40	6475	52,36	58	23	7475	77,31	67	22
5000	32,37	45	07	500	52,84	58	37	500	78,14	67	35
050	32,88	45	34	525	53,29	58	50	525	78,99	67	48
100	33,40	46	01	550	53,75	59	03	550	79,92	68	02
150	33,93	46	28	575	54,25	59	17	575	80,80	68	15
200	34,47	46	55	600	54,72	59	30	600	81,76	68	29
250	35,01	47	22	625	55,24	59	44	625	82,68	68	42
300	35,57	47	49	650	55,72	59	57	650	83,68	68	56
350	36,14	48	16	675	56,25	60	11	675	84,63	69	09
400	36,71	48	43	700	56,74	60	24	700	85,68	69	23
450	37,30	49	10	725	57,28	60	38	725	86,67	69	36
500	37,90	49	37	750	57,79	60	51	750	87,77	69	50
550	38,51	50	04	775	58,35	61	05	775	88,80	70	03
600	39,13	50	31	800	58,88	61	18	7800	89,86	70	16
650	39,76	50	58	825	59,45	61	32
700	40,40	51	25	850	59,99	61	45
5750	41,06	51	52	6875	60,54	61	58

 

Таблица 24

Вычисление поправки гирокомпаса

 

№ п. п.	Дата	Измеренная поправка	Вычисленная поправка
1 2 3 4 5 6 7 8 9 10	26/IX 26/IX 27/IX 28/IX 28/IX 30/IX 1/X 5/X 7/X 10/X	-1°17¢30² -1°16¢53² -1°17¢05² -1°16¢24² -1°16¢48² -1°17¢20² -1°17¢14² -1°16¢38² -1°16¢50² -1°17¢28²	-1°16¢56² -1°16¢54² -1°16¢58² -1°16¢53² -1°16¢58² -1°17¢06²

 

В связи с совершенствованием маркшейдерских гирокомпасов возможны изменения в методике определения дирекционных углов гиросторон. Изменения приводятся в руководстве по эксплуатации соответствующего гироприбора.

Среднюю квадратическую погрешность дирекционного угла гиростороны опреде­ляют по формуле

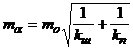,                                                (38)

где m_o - средняя квадратическая погрешность единичного определения гироскопического азимута; k_ш и k_п - число определений гироскопического азимута гиростороны и поправки прибора соответственно.

Погрешность m_o может быть получена по результатам многократного ориентирова­ния, при котором каждый раз определяют гироскопический азимут исходной стороны на земной поверхности и гиростороны в шахте.

Используя результаты гироскопических измерений вычисляют эмпирическую сред­нюю квадратическую погрешность

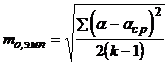,                                             (39)

где k - число измерений дирекционного угла гиростороны.

Построением доверительного интервала оценивают теоретическую среднюю квадратическую погрешность m_o

z₁m_o,эмп< m_o < z₂m_o,эмп,                                                     (40)

где z₁, z₂ - нормированные значения нижнего и верхнего пределов интервала, определяемые по числу степеней свободы r = k - 1 для принятой доверительной вероятности. Числовые значения пределов z выбираются по табл. 25.

Если вычисленная эмпирическая средняя квадратическая погрешность находится в области допустимых значений, определяемых доверительным интервалом, то это свидетельствует о том, что отклонение m_o,эмп от m_o обусловлено ограниченностью измерений и является несущественным.

Эмпирическую среднюю квадратическую погрешность, полученную при числе r>50, можно принимать в качестве приближенного значения теоретической средней квадрати­ческой погрешности измерений.

 

 

Таблица 25

Нижние z₁ и верхние z₂ границы доверительного интервала

z₁m_o,эмп< m_o < z₂m_o,эмп

	Доверительные вероятности
r	0.99		0.95		0.90
	z1	z2	z1	z2	z1	z2
1 2 3 4 5 6 7 8 9 10 15 20 25 30 40 50	0,36 0,43 0,48 0,52 0,55 0,57 0,59 0,60 0,62 0,63 0,67 0,71 0,73 0,75 0,77 0,79	14,14 8,47 4,39 3,48 2,98 2,66 2,44 2,27 2,15 1,81 1,64 1,54 1,47 1,39 1,33	0,45 0,52 0,57 0,60 0,62 0,64 0,66 0,67 0,69 0,70 0,73 0,76 0,78 0,80 0,82 0,84	31,62 6,29 3,73 2,88 2,45 2,20 2,03 1,92 1,83 1,77 1,55 1,45 1,38 1,34 1,28 1,24	0,51 0,58 0,62 0,65 0,67 0,69 0,71 0,72 0,73 0,74 0,78 0,80 0,82 0,83 0,85 0,86	16,01 4,41 3,01 2,43 2,09 1,92 1,80 1,71 1,65 1,60 1,44 1,36 1,31 1,27 1,23 1,20
Пример. Средняя квадратическая погрешность единичного определения гироско­пического азимута из 11 измерений вычислена mo,эмп = 25.4². Требуется при довери­тельной вероятности 0.95 определить доверительные границы для оценки параметра mo. Так как r = 10, то, согласно таблице, имеем: z1 = 0.70, z2 = 1.77, и доверительные пределы будут 0.70´25.4²< mo < 1.77´25.4² или 17.8²< mo < 45².

 

ПРИЛОЖЕНИЕ 18

---

Дата добавления: 2018-04-15; просмотров: 1278; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!