Рациональное распределение ресурсов между альтернативами
Актуальной является задача распределения ресурсов между альтернативами. В частности, интерес представляют задачи комбинаторной оптимизации, самая простая из которых — определение комбинации (альтернатив, проектов), максимизирующей "общие выгоды" при ограничениях на издержки.
Общая постановка задачи определения комбинации альтернатив с максимальной эффективностью (или эффективностью на единицу требуемого ресурса) заключается в определении сочетаний альтернатив, удовлетворяющих следующим целевым функциям:
при выполнении одного из следующих условий:
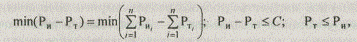
где Э — эффективность рассматриваемой комбинации альтернатив, полученной генерацией множества сочетаний с различным числом альтернатив;
Эi — эффективность i-й альтернативы, входящей в рассматриваемую комбинацию из п альтернатив;
РТ — требуемый ресурс рассматриваемой комбинации альтернатив;
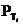— требуемый ресурс i-й альтернативы, входящей в рассматриваемую комбинацию из п альтернатив;
Ри — имеющийся в наличии ресурс рассматриваемой комбинации альтернатив;
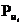— имеющийся в наличии ресурс i-й альтернативы, входящей в рассматриваемую комбинацию из п альтернатив;
С— заданное пороговое значение ресурса.
Эффективность исходного множества альтернатив рассчитывается на основе МАИ и может быть определена либо на одной иерархии, отражающей критерии эффективности, либо на основе отражения значений векторов приоритетов альтернатив, характеризующих выгоды и издержки, получаемые от их реализации.
|
|
|
Существуют ситуации, в которых при распределении ресурсов руководствуются следующим правилом: делать как можно больше при ограниченных (имеющихся в наличии) ресурсах. Целевая функция в данной задаче — обеспечить
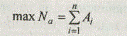
при выполнении одногоиз условий
где Na — число альтернатив;
Аi — альтернатива, на которую распределяется ресурс.
Таким образом, для решения задачи комбинаторной оптимизации необходимо прежде всего сгенерировать множество всех возможных сочетаний (комбинаций) из п-го числа альтернатив. В указанное множество должны входить парные сочетания, тернарные сочетания и далее все п — 1 сочетания, а также сочетание, состоящее из всех п альтернатив. Максимальное число возможных сочетаний NK для данной задачи определяется на основе следующей формулы:
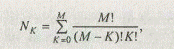
гдеК— число альтернатив в i-й комбинации, принимающеезначение в диапазоне [0,М];
М — максимальное число рассматриваемых альтернатив.
Определим множество комбинаций с различными числом и составом альтернатив.
Допустим, имеется множество из М альтернатив и каждой альтернативе соответствует ее уникальный порядковый номер.
|
|
|
Требуется из заданного множества получить комбинации всех возможных альтернатив, которые должны удовлетворять следующим условиям: 1) в каждой i-й комбинации не должно присутствовать одинаковых альтернатив; 2) каждая i-я комбинация должна отличаться от других не менее чем одной альтернативой; 3) комбинации альтернатив должны содержать в общем случае все единичные, парные, тернарные и другие М-1 и М сочетания альтернатив. Каждой альтернативе в процессе генерации комбинаций присваиваются два типа признаков: "истина" (И) и "ложь" (Л).
В начальном состоянии всем альтернативам присваивается признак "ложь". В этом случае сгенерированная комбинация содержит нуль альтернатив. Далее осуществляется циклическое изменение признаков альтернатив и генерацияиз них новых комбинаций по следующим правилам.
Правило 1. Если альтернатива А1 множества А имеет признак "Л", то изменяем его на признак "И" и заканчиваем изменение признаков у альтернатив. В противном случае, если альтернатива A1 множества А имеет признак "И", осуществляем переход к альтернативе А2.
Правило 2. Если i-я альтернатива Ai множества А имеет признак "Л", то изменяем его на признак "И" и заканчиваем изменение признаков альтернатив. В противном случае изменяем признак i-й альтернативы Аi множества А на "Л" и осуществляем переход к i+1 альтернативе Аi+1.
|
|
|
Правило 3. Если альтернатива АN множества А имеет признак "Л", то изменяем его на "И" и заканчиваем изменение признаков альтернатив. В противном случае, если альтернатива АN имеет значение признака "И", то генерируемая на данной итерации комбинация является последней и содержит все альтернативы множества А.
Таким образом, генерируемая на каждой итерации комбинация включает альтернативы множества А, имеющие на текущей итерации значение признака "Истина".
В табл. 2.11 приведен пример генерации комбинаций с учетом приведенного выше алгоритма для множества А, включающего три альтернативы.
Таблица 2.11
Дата добавления: 2018-04-15; просмотров: 291; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!