ПРОГРАММИРОВАНИЯ СИМПЛЕКС-МЕТОДОМ
Найти максимальное значение линейной функции
Z = x1 + 2x2
при ограничениях
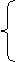 x1 + x2 £ 9
x1 + x2 £ 9
-x1 + x2 £ 3 (17)
x1 - x2 £ 3, x1,x2 ³ 0.
Перейдем от исходной задачи к задаче с ограничениями типа равенств. Введем вектор балансовых переменных y, размерность которого равна числу неравенств в системе ограничений: y = (x3, x4, x5). Все балансовые переменные неотрицательные, в целевой функции им соответствуют коэффициенты, равные нулю. Исходную задачу преобразовали к виду:
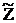 = x1 + 2×x2 + 0×x3 + 0×x4 + 0×x5 ® max
= x1 + 2×x2 + 0×x3 + 0×x4 + 0×x5 ® max
x1 + x2 + x3 = 9
‑x1 + x2 + x4 = 3 (18)
x1 ‑ x2 + x5 =3
x1, x2, x3, x4, x5 ³ 0.
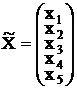 ,
,  ,
, 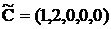 ,
,
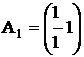 ,
, 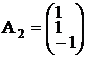 ,
, 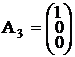 ,
, 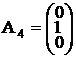 ,
, 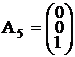 .
.
Заполняем первую симплексную таблицу.
Таблица 3
| Базис | CБ | 
| 1 | 2 | 0 | 0 | 0 |
| B | A1 | A2 | A3 | A4 | A5 | ||
 x3
x4
x5 x3
x4
x5
| 0 0 0 | 9 3 3 | 1 -1 1 | 1 1 -1 | 1 0 0 | 0 1 0 | 0 0 1 |
| Z=0 | -1 | -2 | 0 | 0 | 0 |
Переменные x3, x4, x5 образуют базис. Свободные переменные х1, х2 выбираем равными нулю. Тогда системе ограничений задачи (18) удовлетворяет вектор
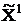 = (0,0,9,3,3)T (сравните значение базисных переменных с вектором В в симплексной таблице).
= (0,0,9,3,3)T (сравните значение базисных переменных с вектором В в симплексной таблице).
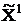 - первая крайняя точка.
- первая крайняя точка.
Так как x3, x4, x5 – базисные переменные, то
CБ = ( 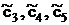 ) = (0,0,0).
) = (0,0,0).
Умножая скалярно вектор CБ и А1 и вычитая из произведения 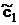 , находим симплексную разность D1. Аналогично, вычисляем остальные симплексные разности Dk (
, находим симплексную разность D1. Аналогично, вычисляем остальные симплексные разности Dk ( 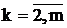 ) в первой крайней точке. Полученные значения записываем в последнюю строку таблицы.
) в первой крайней точке. Полученные значения записываем в последнюю строку таблицы.
|
|
|
Вычислим значение целевой функции в первой крайней точке:
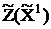 = СБ В = 0
= СБ В = 0
Так как для первой крайней точки имеются отрицательные симплексные разности, то она не является оптимальной. Ищем вторую крайнюю точку. По формуле 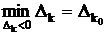 находим переменную, вводимую в базис.
находим переменную, вводимую в базис.
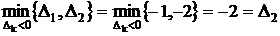 , т.е. в базис надо ввести х2. Т.о. направляющий столбец с номером 2.
, т.е. в базис надо ввести х2. Т.о. направляющий столбец с номером 2.
Определим переменную, выводимую из базиса
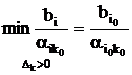 ,
,
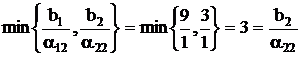 , т.е. i0 = 2.
, т.е. i0 = 2.
Значит, направляющая строка имеет номер 2.
Обратите внимание, что отношение 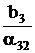 не принималось во внимание при нахождении значения индекса i0, так как значение коэффициента a32 < 0. Переменная, выводимая из базиса х4. Т.о. направляющий элемент a22 = 1.
не принималось во внимание при нахождении значения индекса i0, так как значение коэффициента a32 < 0. Переменная, выводимая из базиса х4. Т.о. направляющий элемент a22 = 1.
Используя один шаг метода Гаусса, введем в базис переменную х2 вместо переменной х4, применяя соотношение (12)-(16). Тем самым найдем координаты второй крайней точки.
Заполняем вторую симплексную таблицу.
Таблица 4
| Базис | CБ | 
| 1 | 2 | 0 | 0 | 0 |
| B | A1 | A2 | A3 | A4 | A5 | ||
 x3
x2
x5 x3
x2
x5
| 0 2 0 | 6 3 6 | 2 -1 0 | 0 1 0 | 1 0 0 | -1 1 1 | 0 0 1 |
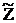 =6 =6
| -3 | 0 | 0 | 2 | 0 |
Сейчас в базисе переменные x3, x2, x5 (порядок именно такой). Свободные переменные х1=0 и х4=0. Тогда базисные переменные принимают значения x3=6, x2=3, x5=6. Вторая крайняя точка 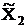 =(0,3,6,0,6)Т. Вектор СБ для этой точки имеет вид:
=(0,3,6,0,6)Т. Вектор СБ для этой точки имеет вид:
|
|
|
CБ = (  ) = (0,2,0).
) = (0,2,0).
Строку симплексных разностей вычисляем по формуле:
Dk = CБAk ‑ 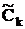 ,
, 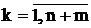
D1 = ‑3, D2 = 0, D3 = 0, D4 = 2, D5 = 0.
Значение целевой функции во второй крайней точке
 = СБ В =0×6 + 2×3 + 0×6 = 6.
= СБ В =0×6 + 2×3 + 0×6 = 6.
Для второй крайней точки одна из симплексных разностей отрицательна, поэтому эта точка еще не является оптимальной.
Находим очередную крайнюю точку. Переменную х1 вводим в базис, так как 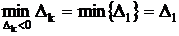 , т.е. направляющий столбец имеет номер 1.
, т.е. направляющий столбец имеет номер 1.
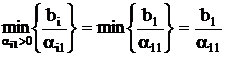 , т.е. i0=1, т.е. направляющая строка имеет номер 1.
, т.е. i0=1, т.е. направляющая строка имеет номер 1.
Тогда переменная х3 - выводится из базиса. Направляющий элемент a11 = 2.
Осуществляем один шаг метода Гаусса, пользуясь соотношениями (12)-(16), получаем третью симплексную таблицу.
Таблица 5
| Базис | CБ | 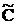
| 1 | 2 | 0 | 0 | 0 |
| B | A1 | A2 | A3 | A4 | A5 | ||
| x1 x2 x5 | 1 2 0 | 3 6 6 | 1 0 0 | 0 1 0 | 0,5 0,5 0 | -0,5 0,5 1 | 0 0 1 |
| Z=15 | 0 | 0 | 1,5 | 0,5 | 0 |
Найдена третья крайняя точка
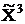 =(3,6,0,0,6)Т,
=(3,6,0,0,6)Т,
CБ = ( 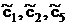 )T = (1,2,0)T,
)T = (1,2,0)T,
D1 = D2 = D5 = 0, D3 =  , D4 =
, D4 = 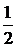 .
.
Так как все симплексные разности неотрицательны, то третья крайняя точка является оптимальной. Значение целевой функции в оптимальной точке равно 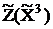 = CБ В = 1×3 + 2×6 + 0×6 = 15.
= CБ В = 1×3 + 2×6 + 0×6 = 15.
|
|
|
Таким образом, найдено оптимальное решение задачи (18). Отбросив в векторе 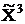 балансовые переменные, получим оптимальное решение исходной задачи Xопт = (3,6), Zmax = 15.
балансовые переменные, получим оптимальное решение исходной задачи Xопт = (3,6), Zmax = 15.
Рассмотрим геометрическую интерпретацию решения. Построим область допустимых решений задачи (17). Это многоугольник ОАВСD.
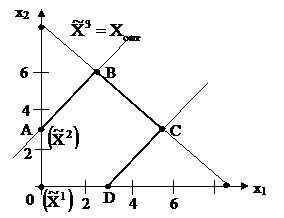 Отметим найденные крайние точки. Первая точка
Отметим найденные крайние точки. Первая точка 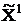 совпадает с вершиной О; вторая – с вершиной А; третья оптимальная точка – вершина В.
совпадает с вершиной О; вторая – с вершиной А; третья оптимальная точка – вершина В.
Найдем решение двойственной задачи.
W = 9U1 + 3U2 + 3U3 ® min,
U1 ‑ U2 + U3 ³ 1
U1 + U2 ‑ U3 ³ 2
U1, U2, U3 ³ 0.
Решение находим по последней симплексной таблице – последние три
симплексные разности Uопт = (1,5; 0,5; 0)
Wmin = 15 [3].
Дата добавления: 2018-04-15; просмотров: 338; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
