ПРИМЕР РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО
Nbsp; МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования "Ижевский государственный технический университет имени М.Т.Калашникова" (ФГБОУ ВПО «ИжГТУ имени М.Т.Калашникова»)
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К выполнению
Лабораторной работы по дисциплине «Теория принятия решений», «Системный анализ»
На тему «Симплексный метод решения задачи
Линейного программирования»
Рекомендовано советом факультета «Информатика и вычислительная техника» к использованию в качестве учебно - методических материалов для студентов
специальности: 230102.65 «Автоматизированные системы обработки информации и управления», специальности: 031301.65 «Теоретическая и прикладная лингвистика», направления: 230100.62 «Информатика и вычислительная техника» в области: «Автоматизированные системы обработки информации и управления», «Системы автоматизированного проектирования»,
форма обучения: очная, заочная
(протокол № 8 от 22.11.2013г. )
Ижевск 2013
Рецензент: Мокроусов М.Н., к.т.н., доцент кафедры АСОИУ.
Составители: Исенбаева Е.Н., старший преподаватель кафедры
АСОИУ.
Рекомендовано советом факультета «Информатика и вычислительная техника» к использованию в качестве учебно- методических материалов для студентов специальности 230102.65 «Автоматизированные системы обработки информации и управления», специальности: 031301.65 «Теоретическая и прикладная лингвистика», направления: 230100.62 «Информатика и вычислительная техника» в области: «Автоматизированные системы обработки информации и управления», «Системы автоматизированного проектирования»,
|
|
|
.
(протокол № 8 от 22.11.2013г. ).
Методические указания к выполнению лабораторной работы на тему «Симплексный метод решения задачи линейного программирования » (теория и варианты заданий) / сост. Е.Н. Исенбаева.- Ижевск, 20013 г.- 17 с.
В методических указаниях описан симплексный метод решения задачи линейного программирования. Сформулирована постановка задачи линейного программирования, рассмотрен алгоритм симплексного метода, проиллюстрированный на примере. Приведены варианты заданий на лабораторную работу.
Учебное пособие предназначено для студентов, обучающихся по специальности 230102.65 «Автоматизированные системы обработки информации и управления», специальности: 031301.65 «Теоретическая и прикладная лингвистика», направления 230100.62 «Информатика и вычислительная техника» в области: «Автоматизированные системы обработки информации и управления», «Системы автоматизированного проектирования», форма обучения очная, заочная.
|
|
|
© Исенбаева Е.Н., составление, 20013
© ФГБОУ ВПО «ИжГТУ имени М.Т. Калашникова, 2013
СОДЕРЖАНИЕ
ВВЕДЕНИЕ.. 4
1. ПОСТАНОВКА ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.. 5
2. АЛГОРИТМ СИМПЛЕКС-МЕТОДА.. 7
3. ПРИМЕР РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО.. 9
ПРОГРАММИРОВАНИЯ СИМПЛЕКС-МЕТОДОМ... 9
4. ЗАДАНИЕ НА ЛАБОРАТОРНУЮ РАБОТУ.. 13
5. СОДЕРЖАНИЕ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ.. 15
6. ВОПРОСЫ ДЛЯ ПРОВЕРКИ ОСТАТОЧНЫХ ЗНАНИЙ.. 16
7.СУЩЕСТВУЮЩИЕ МАТЕМАТИЧЕСКИЕ.. 16
ПРОГРАММНЫЕ СИСТЕМЫ... 16
СПИСОК ЛИТЕРАТУРЫ... 17
ВВЕДЕНИЕ
Данные методические указания предназначены для использования студентами при выполнении лабораторной работы на тему «Симплексный метод решения задачи линейного программирования».
В пособии дается описание распространенного метода решения задачи линейного программирования – симплексного метода. Симплексный метод является классическим и наиболее проработанным методом в линейном программировании. В работе сформулирован алгоритм решения задачи, который проиллюстрирован на примере.
|
|
|
В пособии предложены варианты заданий на лабораторную работу.
Выполняя данную лабораторную работу, студент должен научиться решать задачи линейного программирования и применять полученные навыки при выполнении курсовых работ.
ПОСТАНОВКА ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задача линейного программирования (ЛП) возникает из необходимости оптимально использовать имеющиеся ресурсы. Это задачи, связанные с анализом целей и функций; задачи разработки или совершенствования структур ( производственных структур предприятий, организованных структур объединений); задачи проектирования( проектирование сложных – робототехнических комплексов, гибких производственных систем).
В качестве конкретных примеров задач, которые относятся к области линейного программирования, можно назвать задачу об использовании сырья, задачу об использовании мощностей, задачу на составление оптимальной производственной программы.
Рассмотрим задачу из экономической области на составление оптимальной производственной программы [5]. Для изготовления двух видов продукции Р1, Р2 используется три вида сырья S1, S2, S3. Запасы сырья, количество единиц сырья, затраченных на изготовление единицы продукции, а также величина прибыли, получаемая от реализации единицы продукции, приведены в таблице 1.
|
|
|
Таблица 1
| Вид сырья | Запас сырья, Т | Затраты сырья на единицу продукции | |
| Р1 | Р2 | ||
| S1 | 9 | 1 | 1 |
| S2 | 3 | 0,5 | 1 |
| S3 | 3 | 1 | 0,5 |
| Прибыль от единицы продукции, денежных единиц | 1 | 2 | |
Составить оптимальную производственную программу, т.е. такой план выпуска продукции, чтобы при ее реализации можно было получить максимальную прибыль.
Математически эта задача формулируется следующим образом.
Переменные.
Так как нужно определить объем производства каждого вида продукции, переменными в модели являются:
x1 – объем производства продукции Р1
х2 – объем производства продукции Р2
Целевая функция. Конечную цель задачи- получение максимальной прибыли при реализации продукции – выразим как функцию 2-х переменных х1 и х2.
Суммарная прибыль Z = x1 + 2 x2
Ограничения.
При решении рассматриваемой задачи должны быть учтены ограничения на расход сырья.
х1 + х2 £ 9 (для вида S1),
0,5 х1 + х2 £ 3 (для вида S2),
х1 + 0,5 х2 £ 3 (для вида S3).
Добавим ограничения на не отрицательность значений объемов производства продукции
х1 ³ 0, х2 ³ 0.
Итак, математическая модель формулируется следующим образом.
Определить объемы производства х1, х2 продукции вида Р1 и Р2 в тоннах, при которых достигается максимум целевой функции
Z = х1 + 2 х2
при ограничениях
 х1 + х2 £ 9
х1 + х2 £ 9
0,5 х1 + х2 £ 3
х1 + 0,5 х2 £ 3
Таким образом, задача ЛП заключается в отыскании вектора (х1, х2,…,хJ,…,хn), который максимизирует линейную целевую функцию
Z= с1х1+с2х2+…+сjхj+…+сnхn, (1)
при следующих линейных ограничениях
 a11х1 + a12 х2 + …+a1n xn £ b1
a11х1 + a12 х2 + …+a1n xn £ b1
a21х1 + a22 х2 + …+a2n xn £ b2
. . . (2)
am1х1 + am2 х2 + …+amn xn £ bm
x1 ³0, x2 ³0,. . .,xn ³0. (3)
Запись задачи ЛП в виде (1)-(3) называется симметричной формой представления задачи линейного программирования.
Эту же задачу ЛП можно представить в векторно-матричной записи:
CX ® max
AX £ B, Х ³ 0, где C = (c1, c2,…,cn), 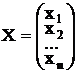 ,
, 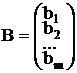 ,
,
A=(aij), 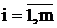 ,
, 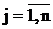 – матрица коэффициентов ограничений,
– матрица коэффициентов ограничений,
С - вектор коэффициентов целевой функции
Х- вектор решения.
Область 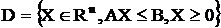 называется областью допустимых значений (ОДЗ) задачи линейного программирования.
называется областью допустимых значений (ОДЗ) задачи линейного программирования.
Соотношения (2), (3) называются системами ограничений задачи ЛП.
Так как 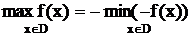 , то можно ограничиться изучением задачи одного типа.
, то можно ограничиться изучением задачи одного типа.
Решением задачи ЛП называется вектор, удовлетворяющий системе ограничений задачи и оптимизирующий целевую функцию.
Другая форма представления задачи ЛП – каноническая. Она имеет вид:
CX ® max
AX = B, X ³ 0.
Наряду с задачей ЛП в симметричной форме (1)-(3) рассмотрим задачу
BU ® min (4)
ATU ³ C, U ³ 0, (5)
где 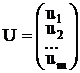 - переменные двойственной задачи.
- переменные двойственной задачи.
Задача (4), (5) называется двойственной по отношению к задаче (1)-(3).
АЛГОРИТМ СИМПЛЕКС-МЕТОДА
Симплекс метод является наиболее распространенным вычислительным методом, который может быть применен для решения любых задач ЛП как вручную, так и с помощью ЭВМ.
Этот метод позволяет переходить от одного допустимого решения к другому, причем так, что значения целевой функции непрерывно возрастают. В результате оптимальное решение находят за конечное число шагов. Алгоритм симплекс-метода позволяет также установить является ли задача ЛП разрешимой.
1. Рассмотрим задачу ЛП в симметричной форме (1)-(3). Сделаем допущения: В ³ 0.
Введем вектор Y такой, что Y = B ‑ AX, YÎRm, Y ³ 0,
Y = (xn+1, xn+2, . . .,xn+m)T. Вектор Y называют балансовым, а xn+1, xn+2, . . .,xn+m – балансовыми переменными.
В целевую функцию балансовые переменные входят с нулевыми коэффициентами, т.е.
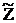 =c1x1 + c2x2 +…+ cnxn + 0xn+1 +…+ 0×xn+m
=c1x1 + c2x2 +…+ cnxn + 0xn+1 +…+ 0×xn+m
или
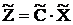 , где
, где 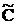 ,
,  Î Rn+m. (6)
Î Rn+m. (6)
Систему ограничений (2) задачи ЛП можно записать:
 a11х1 + a12 х2 + …+a1n xn +хn+1 = b1
a11х1 + a12 х2 + …+a1n xn +хn+1 = b1
a21х1 + a22 х2 + …+a2n xn +хn+2 = b2
. . . (7)
am1х1 + am2 х2 + …+amn xn +хn+m = bm
причем xj ³ 0, 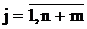 (8)
(8)
Таким образом, задачу ЛП (1)-(3) преобразовали из симметричной формы в каноническую.
Итак, вместо задачи (1)-(3) будем искать решение задачи (6)- (8).
2. Положим j = 1. Взяв переменные х1,…,хn за свободные и положив их равными нулю, а хn+1,…,хn+m – за базисные, находим первую крайнюю точку.
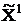 = (0,…,0,b1,b2,...,bm).
= (0,…,0,b1,b2,...,bm).
n
3. Обозначим через Аk - вектор, составленный из коэффициентов ограничений при переменной хk, СБ ‑ вектор, составленный из коэффициентов целевой функции, соответствующих базисным переменным, через Сk – коэффициент целевой функции при переменной xk.
Вычислим симплексные разности Dk в j-той крайней точке по формуле
Dk = Ak∙ CБ ‑  k,
k, 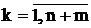 . (9)
. (9)
Заполняется симплекс-таблица (таблица 2) по указанным выше правилам.
Таблица 2
| Базис | СБ | 
|  1 1
| 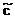 2 2
| … | 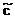 n n
| 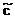 n+1 n+1
| … | 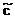 n+m n+m
|
| B | A1 | A2 | … | An | An+1 | … | An+m | ||
| xn+1 xn+2 . . . xn+m | 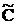 n+1 n+1
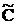 n+2
.
.
. n+2
.
.
.
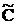 n+m n+m
| b1 b2 . . . bm | a11 a21 . . . am1 | a12 a22 . . . am2 | … … . . . … | a1n a2n . . . amn | 1 0 . . . 0 | … … . . . … | 0 0 . . . 1 |
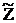
| D1 | D2 | … | Dn | Dn+1 | … | Dn+m |
4. Если для j-той крайней точки все симплексные разности Dk ³0, 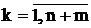 , то эта точка оптимальная. Конец решения.
, то эта точка оптимальная. Конец решения.
Если есть столбец, в котором симплексная разность Dk0 £ 0 и все элементы столбца aik0 £ 0, 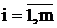 , то задача ЛП решения не имеет, т.к. целевая функция не ограничена сверху.
, то задача ЛП решения не имеет, т.к. целевая функция не ограничена сверху.
В остальных случаях переход к пункту 5.
5. Находим k0 ‑ направляющий столбец. Выбираем столбец, в котором самая минимальная симплекс разность среди отрицательных симплекс-разностей (напомним, что решаем задачу максимизации) т.е.
Dk0= min Dk (10)
Dk < 0.
Направляющая строка i0 выбирает из условия
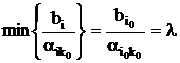 ,
, 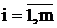 , αik0 › 0 . (11)
, αik0 › 0 . (11)
Итак, направляющий элемент ai0k0.
Заполняем таблицу, соответствующую новому решению.
6. Выполняем один шаг метода Гаусса, введя в базис вектор Аk0 вместо вектора Аn0, имеющего i0 – координату, равную 1. Для это используются следующие соотношения:
- новые элементы направляющей строки :
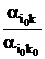 ,
, 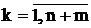 ; (12)
; (12)
- новые элементы направляющего столбца:
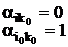 ,
, 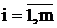 , причем i ¹ i0; (13)
, причем i ¹ i0; (13)
т.е. в направляющем столбце все элементы равны 0, а направляющий элемент равен 1.
- новые значения остальных элементов матрицы:
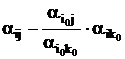 ,
, 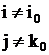 ; (14)
; (14)
- новые значения симплексных разностей:
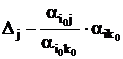 ,; (15)
,; (15)
Правильность вычислений контролируется по формулам непосредственного счета:
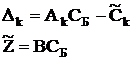 ,
, 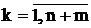 (16)
(16)
Получаем (j + 1) крайнюю точку. Полагая j = j + 1, переходим к пункту 4.
Построение симплекс-таблиц продолжается до тех пор, пока не будет получено оптимальное решение.
Замечание 1. Если одна из базисных переменных равна нулю, то крайняя точка, соответствующая такому базисному решению- вырожденная. Вырожденность возникает, когда имеется неоднозначность в выборе направляющей строки. Можно вообще не заметить вырожденности задачи, если выбрать другую строку в качестве направляющей. В случае неоднозначности нужно выбирать строку с наименьшим индексом, чтобы избежать зацикливания.
Замечание 2. Пусть в некоторой крайней точке все симплексные разности неотрицательные Dk ³ 0 ( 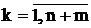 ),т.е. получено оптимальное решение и существует такой Аk – небазисный вектор, у которого Dk = 0. Тогда максимум достигается по крайней мере в двух точках, т.е. имеет место альтернативный оптимум. Если ввести в базис эту переменную xk, значение целевой функции не изменится.
),т.е. получено оптимальное решение и существует такой Аk – небазисный вектор, у которого Dk = 0. Тогда максимум достигается по крайней мере в двух точках, т.е. имеет место альтернативный оптимум. Если ввести в базис эту переменную xk, значение целевой функции не изменится.
Замечание 3. Решение двойственной задачи находится в последней симплексной таблице. Последние m компонент вектора симплексных разностей( в столбцах балансовых переменных) – оптимальное решение двойственной задачи. Значение целевых функций прямой и двойственной задачи в оптимальных точках совпадают.
Замечание 4. При решении задачи минимизации в базис вводится вектор с наибольшей положительной симплексной разностью. Далее применяется тот же алгоритм, что и для задачи максимизации[3].
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО
Дата добавления: 2018-04-15; просмотров: 363; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
