Оценка погрешности интерполяционных формул
Погрешность формулы Лагранжа
погрешность формулы Лагранжа можно записать в общем виде:
 , (2.17)
, (2.17)
надо отметить, что точка  лежит внутри отрезка
лежит внутри отрезка  .
.
Формула (2.17) справедлива для всех точек отрезка  , в том числе и для узлов интерполяции. Обозначим за
, в том числе и для узлов интерполяции. Обозначим за  , тогда формулу (2.17) можно переписать
, тогда формулу (2.17) можно переписать
 . (2.18)
. (2.18)
Пример. С какой точностью можно вычислить  с помощью квадратичной интерполяционной формулы Лагранжа, если узлы интерполяции
с помощью квадратичной интерполяционной формулы Лагранжа, если узлы интерполяции 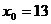 ,
,  ,
, 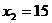 .
.
Так как полином квадратичный, для оценки погрешности нам потребуется вычислить третью производную функции  :
:
первая производная функции  :
:  ,
,
вторая производная функции  :
:  ,
,
третья производная функции  :
:  .
.
Оценим константу  .
.
Оценим погрешность: 
Ответ:  .
.
Погрешность формулы Ньютона
Пусть  ,
,  , …,
, …,  - узлы интерполяции, равноотстоящие друг от друга, т.е.
- узлы интерполяции, равноотстоящие друг от друга, т.е.  ,
, 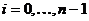 . Множество
. Множество  . Требуется оценить погрешность формулы Ньютона.
. Требуется оценить погрешность формулы Ньютона.
Если обозначить за q выражение: 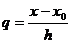 . Тогда, воспользовавшись формулой (2.18), для первой интерполяционной формулы Ньютона остаточный член или погрешность будет иметь вид:
. Тогда, воспользовавшись формулой (2.18), для первой интерполяционной формулы Ньютона остаточный член или погрешность будет иметь вид:
 , где
, где  .
.
Если же требуется найти остаточный член второго интерполяционного полинома Ньютона, то в качестве 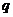 берется выражение:
берется выражение:  , тогда погрешность:
, тогда погрешность:
 , где
, где  .
.
Вообще говоря,  в случае интерполяции; при экстраполяции возможен случай
в случае интерполяции; при экстраполяции возможен случай 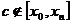 .
.
Если предположить, что h достаточно мало и по определению производной функции  , можно положить
, можно положить  . Следовательно, погрешность первого интерполяционного полинома Ньютона:
. Следовательно, погрешность первого интерполяционного полинома Ньютона:
|
|
|
 , (2.19)
, (2.19)
а погрешность второго интерполяционного полинома Ньютона:
 . (2.20)
. (2.20)
Пример. По таблице значений функции  на отрезке
на отрезке 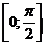 построить полином Ньютона 2‑ой степени и вычислить приближенное значение в точке
построить полином Ньютона 2‑ой степени и вычислить приближенное значение в точке  .
.
Возьмем четыре равноудаленные друг от друга точки на отрезке 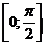 и составим таблицу значений:
и составим таблицу значений:
| i | x | y | 
| 
| 
|
| 0 | 0 | 0 | 0,5 | -0,144 | 0,088 |
| 1 | 
| 
| 0,366 | -0,232 | |
| 2 | 
| 
| 0,134 | ||
| 3 | 
| 1 |

 .
.
 .
.
 .
.
Ответ:  ,
,  .
.
Приближение функций. Аппроксимирование функций
Напомним постановку задачи аппроксимации. Рассмотрим функцию 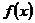 . Задача аппроксимации ставится следующим образом: данную функцию
. Задача аппроксимации ставится следующим образом: данную функцию 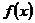 требуется заменить другой функцией
требуется заменить другой функцией  так, чтобы отклонение (ошибка), в некотором смысле, функции
так, чтобы отклонение (ошибка), в некотором смысле, функции 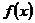 от
от  на заданном множестве
на заданном множестве 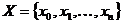 было наименьшим. Как правило, в качестве аппроксимирующей функции выбирается полином
было наименьшим. Как правило, в качестве аппроксимирующей функции выбирается полином  . Тогда полином
. Тогда полином  называется аппроксимирующим, а сама задача аппроксимациисводится к нахождению коэффициентов
называется аппроксимирующим, а сама задача аппроксимациисводится к нахождению коэффициентов 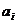 i=0,1,…,m полинома
i=0,1,…,m полинома  , причем таких, что отклонение
, причем таких, что отклонение  (в некотором смысле) функции от полинома было минимальным.
(в некотором смысле) функции от полинома было минимальным.
|
|
|
Среднеквадратичная полиномиальная аппроксимация
При точечном среднеквадратичном аппроксимировании за меру отклонения полинома  от данной функции
от данной функции 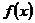 на множестве точек
на множестве точек 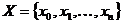 берется квадратичное отклонение:
берется квадратичное отклонение:
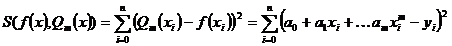
 (3.1).
(3.1).
Такой способ аппроксимирования называют еще методом наименьших квадратов. Проблема состоит в том, чтобы выбрать коэффициенты  ,
, 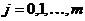 полинома
полинома  так, чтобы отклонение (ошибка)
так, чтобы отклонение (ошибка)  была наименьшей.
была наименьшей.
Предполагается, что степень m полинома  не больше количества точек n во множестве
не больше количества точек n во множестве  ,
,  . В предельном случае, если
. В предельном случае, если  , задача аппроксимации сводится к задаче интерполирования функции
, задача аппроксимации сводится к задаче интерполирования функции  полиномом
полиномом  . В этом случае, ошибка
. В этом случае, ошибка  равна нулю, т.е. в узлах
равна нулю, т.е. в узлах 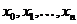 значение функции
значение функции  совпадает со значением полинома
совпадает со значением полинома  ,
,  . Коэффициенты
. Коэффициенты  ,
, 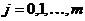 полинома
полинома  ищутся из системы линейных алгебраических уравнений (СЛАУ):
ищутся из системы линейных алгебраических уравнений (СЛАУ):
 .
.
Если все 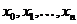 различны, то система имеет единственное решение, и однозначно определяется полином
различны, то система имеет единственное решение, и однозначно определяется полином  .
.
В случае если  , СЛАУ несовместна. Отклонение
, СЛАУ несовместна. Отклонение  не равно нулю. Для нахождения коэффициентов полинома используем условие минимизации ошибки
не равно нулю. Для нахождения коэффициентов полинома используем условие минимизации ошибки  . Дифференцируем выражение (3.1) по переменным
. Дифференцируем выражение (3.1) по переменным  и приравниваем производные к нулю и получаем следующую систему из m+1 уравнений c m+1 неизвестным:
и приравниваем производные к нулю и получаем следующую систему из m+1 уравнений c m+1 неизвестным:
|
|
|


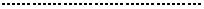 (3.2)
(3.2)
 .
.
Вводим дополнительные обозначения:  ,
,  и
и  ,
, 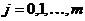 . Заметим, что
. Заметим, что  . Система (3.2) имеет вид:
. Система (3.2) имеет вид:
 , (3.3)
, (3.3)
Если точки 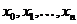 различны и
различны и  , то определитель матрицы (3.3) равен нулю, и система имеет единственное решение. Полином с такими коэффициентами
, то определитель матрицы (3.3) равен нулю, и система имеет единственное решение. Полином с такими коэффициентами  будет обладать наименьшим квадратичным отклонением
будет обладать наименьшим квадратичным отклонением  .
.
Рассмотрим частные случаи.
Пример 2. Воспользовавшись таблицей значений функции из первого примера, построить аппроксимирующий полином второй степени. Вновь составляем таблицу, но в этом случае надо добавить суммы  :
:

| 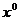
| 
| 
| 
| 
| 
| 
| 
|
| 0 | 1 | -2 | 4 | -8 | 16 | 0 | 0 | 0 |
| 1 | 1 | -1 | 1 | -1 | 1 | 3 | -3 | 3 |
| 2 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 |
| Суммы | 
| 
| 
| 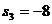
| 
| 
| 
| 
|
Для аппроксимирующего полинома второй степени получаем систему уравнений размером три на три:
 , решая ее, получаем коэффициенты
, решая ее, получаем коэффициенты  . Следовательно, аппроксимирующий полином второй степени имеет вид:
. Следовательно, аппроксимирующий полином второй степени имеет вид:  .
.
|
|
|
Ответ:  .
.
Дата добавления: 2018-04-15; просмотров: 2178; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
