Первая интерполяционная формула Ньютона
Приближение функций. Интерполирование функций
Постановка задачи аппроксимации
Пусть задана система функций: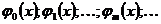 
, которые являются непрерывными и дифференцируемыми.
Определение. Обобщенными многочленами или обобщенными полиномами называются функции вида
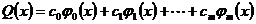, (2.1)
где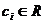 
, i=0,1,…,m – постоянные коэффициенты полинома.
Рассмотрим функцию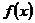 
. Задача о приближении ставится следующим образом: данную функцию 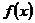требуется заменить обобщенным полиномом 
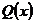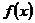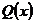так, чтобы отклонение (ошибка), в некотором смысле, функции от на заданном множестве 
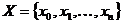было наименьшим. Такая замена называется аппроксимацией. Этого можно достичь за счет подбора коэффициентов обобщенного полинома 
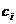. Тогда полином 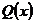называется аппроксимирующим.
Определение. Вообще говоря, аппроксимацией называется замена одной функции 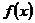на другую 
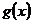, так чтобы отклонение 
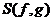(в некотором смысле) функций друг от друга было минимальным.
Если множество X состоит из отдельных точек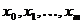 
, то приближение называется точечным, если X является отрезком 
, 
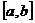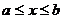, то приближение называется интегральным.
На практике часто в качестве системы функций 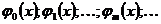используется последовательность степенных функций: 
, 
, …, 
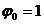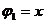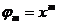. Тогда полином 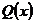имеет вид:
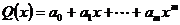, (2.2)
где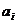 
i=0,1,…,m – коэффициенты полинома. В этом случае получаем задачу аппроксимации функции 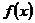каноническим полиномом .
|
|
|
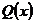Постановка задачи интерполяции
Рассмотрим отрезок 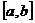. На нем заданы n+1 точки 
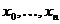, которые называются узлами интерполяции, и значения некоторой функции 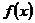в этих точках:
, 
, …, 
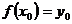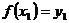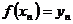(2.3)
Задача интерполяции: требуется построить некоторую функцию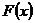 
, которая называется интерполяционной функцией, принадлежащую некоторому известному классу, т.е. имеющую определенные свойства, и принимающую в узлах интерполяции те же значения, что и :
, 
, …, 
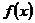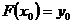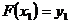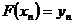, (2.4)
Таким образом, надо найти кривую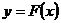 
некоторого определенного типа, проходящую через заданную систему точек 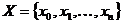. В такой общей постановке задача может иметь бесконечное множество решений или совсем их не иметь. Но задача становится однозначной, если вместо произвольной функции 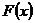искать полином 
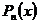степени не выше n, удовлетворяющий условиям (2.4), то есть
, …, 
.
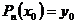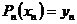Полученную интерполяционную функцию 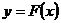или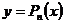 
обычно используют для приближенного вычисления значений функции 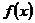в точках, отличных от узлов интерполяции. Такая операция называется интерполированием функции 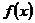. При этом различают интерполирование, когда 
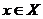, и экстраполирование, когда 
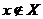. В дальнейшем под термином интерполирование мы будем понимать обе операции.
|
|
|
Надо отметить, что интерполяция является частным случаем аппроксимации.
Первая интерполяционная формула Ньютона
Вводные замечания
Введем следующие обозначения.
Пусть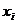 
, i=0,1,…,n - равноотстоящие узлы интерполяции, т.е. 
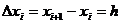, i=0,1,…,n-1, где h - const – шаг интерполяции (приращение аргумента). Выражение вида:
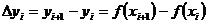, i=0,1,…,n-1 называется первой конечной разностью,
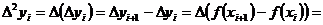
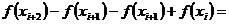
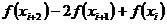, i=0,1,…,n-2 - вторая конечная разность.
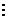
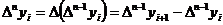- конечная разность n‑го порядка.
Дата добавления: 2018-04-15; просмотров: 479; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!