Системы счета времени: местное, всемирное, поясное, летнее идекретноевремя. Долгота. Линия перемены даты. Календари. Юлианские дни.
Время определяется в некоей системе отсчёта, которая может быть как неравномерная, так и равномерная. Равномерная эталонная система отсчёта выбирается «по определению»Это определение — не произвольное, а связанное с наиболее точными периодическими процессами, доступными человечеству на данном этапе развития экспериментальной физики:
Ме́стное вре́мя — одинаковое время в один момент суток в точках, расположенных на одном меридиане.
Конкретно, под местным временем могут пониматься:
Поясное время в данном конкретном месте, Среднее солнечное время на данном меридиане;Местное солнечное время на данном меридиане с учётом изменяемой продолжительности астрономических суток, и отсчитываемое от моментов астрономических полуночи и полудня.
Всеми́рное координи́рованное вре́мя (UTC) — стандарт, по которому общество регулирует часы и время. Отличается на целое количество секунд от атомного времени и на дробное количество секунд от всемирного времени UT1.
UTC было введено вместо устаревшего среднего времени по Гринвичу (GMT). Новая шкала времени UTC была введена, поскольку шкала GMT является неравномерной шкалой и связана с суточным вращением Земли. Шкала UTC основана на равномерной шкале атомного времени (TAI) и является более удобной для гражданского использования.
Так как между UTC и UT1 разница не превышает 0,9 с, если не требуется высокая точность, может использоваться более общее понятие Всемирное время (UT).
|
|
|
Часовые пояса вокруг земного шара выражаются как положительное и отрицательное смещение от UTC.
Следует помнить, что время по UTC не переводится ни зимой, ни летом. Поэтому для тех мест, где есть переход на летнее время, смещение относительно UTC меняется.
Географический часово́й по́яс — полоса на земной поверхности шириной ровно 15° (± 7,5° относительно среднего меридиана). Средним меридианом нулевого часового пояса считается гринвичский меридиан.
Административный часово́й по́яс — участок земной поверхности, на котором в соответствии с некоторым законом установлено определённое поясное время.
Формирование административных часовых поясов связано со стремлением, с одной стороны, учитывать вращение Земли вокруг своей оси, а с другой стороны, определить территории (временные зоны) с примерно одинаковым местным временем таким образом, чтобы различия во времени между ними были кратны одному часу. Существуют некоторые страны, в которых местное время отличается от всемирного не только на целое количество часов, но ещё дополнительно на 30 или 45 мин. Правда, такие временные зоны не являются стандартными часовыми поясами.
|
|
|
На Северном и Южном полюсах меридианы сходятся в одной точке, и поэтому там понятие часовых поясов, а заодно и местного времени, теряет смысл. Считается, на полюсах должно использоваться всемирное время, однако на станции Амундсен-Скотт (Южный полюс) действует время Новой Зеландии.
Ле́тнее вре́мя — время, сдвинутое на 1 час вперёд относительно времени, принятого в данном часовом поясе. Вводится во многих странах в летний период с целью экономии электроэнергии на освещение. В зимний период время «сдвигают» обратно. В большинстве стран время в зимний период совпадает со стандартным астрономическим временем часового пояса, хотя есть и исключения из этого правила.
Декре́тное вре́мя является одним из способов использования в стране или на какой-либо территории такого времени, которое опережает время своего географического часового пояса на один час.
Формальной отличительной особенностью применения декретного времени от иных способов использования опережающего времени является добавление к поясному времени т. н. «декретного часа» при формальном сохранении нумерации часовых поясов.
Долгота́: Долгота λ — это угол между плоскостью меридиана, проходящего через данную точку, и плоскостью нулевого меридиана. Используется в ряде систем сферических координат, определяет положение точек на поверхности Земли, Солнца, планет и на небесной сфере относительно нулевого меридиана, от которого ведётся отсчёт долгот.
|
|
|
Выбор нулевого меридиана произволен и определяется соглашением.
Долготы от 0 до 180° к востоку от нулевого меридиана называют восточными, к западу — западными. Восточные долготы принято считать положительными, западные долготы — отрицательными.
Ли́ния переме́ны да́ты — условная линия на поверхности земного шара, проходящая от полюса до полюса, по разные стороны которой местное время отличается на сутки (или почти на сутки).
Примерно соответствуя меридиану 180°, проходящему в основном по океану, на практике линия перемены дат определена местами довольно плохо. Линия перемены даты нигде, кроме Антарктиды, не проходит по суше, хотя есть случаи, когда она проведена между близко расположенными островами
При пересечении линии перемены даты в направлении из Западного Полушария в Восточное, в счете календарных дат прибавляют один день (переходят к завтрашней дате); при движении же из Восточного в Западное — возвращаются на один день назад (переходят ко вчерашней дате). Перемена дат должна осуществляться только при использовании, в той или иной форме, местного времени. Непонимание этого обстоятельства приводит к «парадоксам» касательно обхода земного полюса по кругу или облёта Земли по орбите.
|
|
|
Календа́рь — система счисления больших промежутков времени, основанная на периодичности движения небесных тел: Солнца — в солнечных календарях, Луны — в лунных календарях и одновременно Солнца и Луны в лунно-солнечных календарях.
Счёт года с 1 января был введён в Риме Юлием Цезарем в 45 году до н. э. (юлианский календарь). В 325 году юлианский календарь был принят Византией. На Руси с 1492 года началом года стало считаться не 1 марта, а 1 сентября.
Юлианский календарь установил среднюю продолжительность года в 365,25 суток: обычные годы длились 365 дней, один раз в четыре года (високосный год) — 366 дней.
Современный календарь назван григорианским (новый стиль). Он введён при папе римском Григории XIII 15 октября 1582 года взамен юлианского календаря (старого стиля). Реформа, которую провёл Григорий XIII и признали в большинстве католических стран, состояла из двух частей:
1) Была устранена ошибка в 10 дней, накопившаяся со времен I Вселенского собора (325 год), на котором были установлены правила вычисления христианской Пасхи.
2) На будущее же была введена поправка, обеспечивающая более точное соответствие с солнечным исчислением, которая заключается в том, что из каждых 400 лет должны были быть исключены три високосных года. Таким образом, ошибка в один день накапливается лишь через 3333 года. Исключение трёх високосных лет за четыре века достигалось следующим правилом. Если номер года заканчивается не на два нуля, то он считается високосным тогда, когда номер года кратен четырём (например, 1996, 2004, 2008 годы). Если год заканчивается на два нуля, то он високосный только тогда, когда число сотен в нём также кратно четырём (например, 1600, 2000, 2400 годы). Во всех остальных случаях год считается невисокосным
Факторы, искажающие положения светил на небе. Рефракция. Суточная игодичная аберрации. Суточный и годичный параллаксы. Собственные движения звёзд. Единицы измерения расстояний в астрономии. Методы определения расстояний до светил и размеров небесных тел Солнечной системы.
Рефракция
В результате преломления лучейсвета в атмосфере наблюдательвидит светило в точке M1, а не вточке M2 в случае отсутствия
Атмосферы.
Явление преломления световыхлучей при прохождении имиземной атмосферы называетсяастрономической рефракцией∠M1OM2 = ρ (угол рефракции)
∠ZOM1 = z' (видимое зенитноерасстояние)
∠ZOM2 = z (истинное зенитноерасстояние)
• Рефракция «приподнимает» светила над горизонтом
• Рефракция не изменяет азимутов светил и, очевидно, равна нулю
для светил в зените
• В кульминации рефракция искажает склонение, но не искажает
прямое восхождение
• Вследствие рефракции наблюдается изменение формы дисков
Солнца и Луны при их восходе и закате. Рефракция нижних краёвдисков у горизонта почти на 6' больше рефракции верхних краёв,а, т.к. горизонтальные диаметры рефракцией не изменяются, товидимые диски Солнца и Луны принимают овальную форму
• На горизонте ρ = 35'
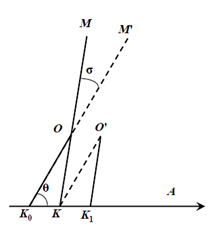Суточная и годичная аберрации
Аберрацией светила называется явление,состоящее в том, что движущийсянаблюдатель видит светило не в томнаправлении, в котором он видел бы его втот же момент, если бы находился в покое∠M'K0A = θ (угловое расстояние видимогонаправления на звезду от точки неба, вкоторую направлена скоростьнаблюдателя)
∠M'OM = σ (аберрационное смещение)
Суточная аберрация – следствие конечности скорости света в сочетании
со скоростью суточного вращения наблюдателя, годичная – всочетании со скоростью годичного движения, т.е. движения Земли поорбите (v = 29,78 км/с)σ = 20,50'' sin θ
Суточный параллакс
Координаты одного и того же небесноготела, определённые с Земли, разные вразличных точках её поверхности. Такиекоординаты называются топографическими.
Зависимость координат светила от точкинаблюдения на Земле связана со смещениемпроекции светила на небесной сфере,которое называется параллаксом.
Основным считается направление насветило из центра Земли.Такое направление даёт геоцентрическое положение светила и определяет егогеоцентрические координаты.
Суточный параллакс – это угол, под которым со светила был бы виден радиусЗемли. Для светила в зените параллакс равен нулю.
Если светило наблюдается на горизонте, то суточныйпараллакс принимает максимальное значение иназывается горизонтальным параллаксом p. p' = p sin z'
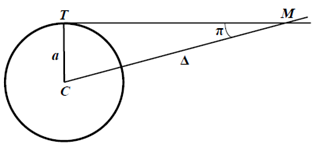Годичный параллакс
Угол, под которым со звезды был бывиден средний радиус земной орбитыa при условии, что направление на
звезду перпендикулярно радиусу,называется годичным параллаксом πзвезды.
Расстояние до звезды:
Т.к. параллаксы всех звёзд меньше 1'', то:
Окончательно:
Расстояние Δ получается в тех же единицах, в которых выраженсредний радиус земной орбиты a
Собственным движением называются изменения координат звёзд на небесной сфере, вызванные относительным движением звёзд и Солнечной системы. В них не включают периодические изменения, вызванные движением Земли вокруг Солнца (параллакс).
Более строгое определение: «Собственным движением звезды в астрономии называют величины, характеризующие её угловое перемещение на небесной сфере в заданной системе координат за единицу времени»
Если какая-либо звезда наблюдалась дважды в эпоху t1 и эпоху t2 и её видимые координаты — прямое восхождение (α) и склонение (δ) то её собственное движение определяется как
размерность — секунда времени в год,
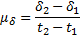
размерность — угловая секунда в год.
Определённые таким способом собственные движения звёзд иногда называют меридианными, так как они определяются в результате сравнения двух положений, полученных посредством наблюдений на меридианных кругах.
Единицы измерения расстояний вастрономии
• Астрономическая единица (а.е.) – среднее расстояниеЗемли от Солнца (средний радиус земной орбиты).
1 а.е. = 149 600 000 км
• Парсек (пк) – расстояние, соответствующее годичномупараллаксу в 1''
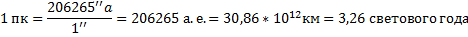
• Световой год – расстояние, которое свет в вакуумепроходит за один год
Методы определения расстояний до светил
• Определение расстояний до тел Солнечной системы основано на измеренииих суточных горизонтальных параллаксов
• Суточный горизонтальный параллакс светила можно определить, измеривпрямое восхождение светила α из одного и того же места на Земле, но вразличные моменты времени
• Расстояния до тел Солнечной системы можно определять такжерадиолокационными методами
• Расстояния до звёзд определяются по их годичному параллактическомусмещению. В этом случае измеряются геоцентрические координаты звезды изнаблюдений, произведённых в двух различных точках орбиты Землиприблизительно через полгода одно после другого
• Наилучшие современные определения годичных параллаксов выполняются скосмических аппаратов, при этом достигается точность в 0,001"
Метод определения размеров небесных телСолнечной системы
На основе измеренныхгоризонтальных параллаксов
можно определить линейныеразмеры небесных тел
Солнечной системы
ρ – угловой радиус светила (половина угла, под которым с Земли видендиск светила),
R0 – линейный радиус Земли, r – линейный радиус светила,
p0 – горизонтальный экваториальный параллакс светилаr = Δ sin ρ, R0 = Δ sin p0
Практические задачи астрометрии. Определение всемирного времени. Поправка часов. Ход часов. Определение географической долготы. Определение географической широты и поправки часов. Абсолютные и относительные методы измерения экваториальных координат.Астрономические каталоги, карты и атласы звёздного неба.
Практические задачи астрометрии:
• Определение точного времени
• Определение географических координатпунктов на поверхности Земли
• Измерение точных координат светил
Определение всемирного времени. Поправка часов. Ход часов.Определение географической долготы
Разность между временем T в какой-то момент по стандартной шкале ипоказаниями рабочих часов T' в этот момент называется поправкой часов u:u = T – T' или T = T' + u
Изменение поправки часов за определённый промежуток времени называетсяходом часов ω:
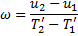
В начале, с помощью астрономических наблюдений определяется местное звёздное время(s), которое далее пересчитывается в среднее солнечное, т.е. в точное время (T):s = α + t = T = T' + u или u = α + t – T'
Если отметить показания часов T' в момент верхней кульминации (t = 0), тоu = α – T'
Зная поправку часов u, определяют всемирное время (Universal Time, UT).
Из сравнения шкал всемирного и атомного времени определяютнеравномерность вращения Земли
Определение географической долготы λ сводится к вычислению разностиместного времени на данном географическом меридиане и временигринвичского меридиана:λ = Tm – T0 = u – u0
Определение географической широты и поправки часов
1) Определение φ и u по измеренным зенитным расстояниям
cos z = sin φ sin δ + cos φ cos δ cos t и t = T' + u – α (1)
Если для двух (или более) светил, для которых по Астрономическомуежегоднику известны α и δ, измерены z (или h) по звёздным часам в моментвремени T', то по (1) можно найти φ и u.
2) Определение φ и u в момент кульминации (t = 0 или 12h)
Для верхней кульминации к югу от зенита: φ = δ + z (2)
Для верхней кульминации к северу от зенита: φ = δ – z (3)
Для нижней кульминации: φ = 180 – δ – z (4)
Т.о., по известному δ и измеренному z из (2) – (4) определяют широту
Поправка часов для верхней кульминации: u = α – T' (5)
Поправка часов для нижней кульминации: u = α – T' + 12h (6)
Абсолютные и относительные методы измеренияэкваториальных координат.
Абсолютный метод определения склонений
Измеряются зенитные расстояния незаходящейзвезды в верхней и нижней кульминации:
zв.к. = δ –φ и zн.к. = 180 – φ – δОткуда: δ = 90 – 0,5 (zн.к. – zв.к.) и φ= 90 – 0,5 (zн.к. + zв.к.)
Т.е. определена широта места наблюдения и склонение однойзвезды. Аналогичным образом находятся φ и δ для несколькихнезаходящих звёзд, и значение φ усредняется. Далее поформулам (2) – (4) находятся склонения других звёзд (в т.ч. изаходящих).
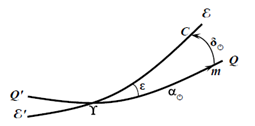Абсолютный метод определения прямых восхождений
ε ε' – эклиптика, QQ' – небесный экватор, ε – наклонение эклиптики к экватору(угол между плоскостями), mC – склонение центра Солнца δ (дугана поверхности сферы), ϒm – прямое восхождение Солнца α. Сферический треугольник ϒmC – прямоугольный, поэтому:
Вблизи дней солнцестояний (т.е. когда δŸ принимает экстремальныезначения) проводят измерения δсолнца, абсолютная величина которого = ε.Далее вычисляется αсолнца и s = αсолнца = T'солнца + u, т.е. поправка часов.Выбираются 30 – 40 ярких звёзд, равномерно расположенных вдольэклиптики и небесного экватора, и которые можно наблюдать до или посленаблюдений Солнца. Такие звёзды называются часовыми.При наблюдении часовых звёзд определяют их моменты прохождениячерез меридиан (кульминации): T'1, T'2, …, T'n.При наблюдении Солнца определяется момент его прохождения черезмеридиан T'солнца и зенитное расстояние в этот момент zсолнца. Далее вычисляетсяδсолнца и αсолнца, а также поправки и ход часов на каждый день наблюдения.
Для каждого дня наблюдения составляют уравнения для Солнца ичасовых звёзд: αсолнца = T'солнца + u, α1 = T'1 + u1, …, αn = T'n + un.
В уравнении для Солнца известны все величины, а в уравнениях длячасовых звёзд – величины T'i и поправки часов: ui = u + ω(T'i – T'Ÿ).Т.о. можно определить прямые восхождения звёзд абсолютным методом:
αi = T'i + u + ω(T'i – T'Ÿ).
В этом методе наблюдения Солнца необходимы для фиксации положенияточки ¢ среди звёзд. С этой целью вместо Солнца можно наблюдатьлюбую планету (в т.ч. и малую) Солнечной системы.
Относительные методы
В относительных методах определениекоординат сводится к измерениюразностей Δδ и Δα определяемых и
опорных звёзд:T – Ti = α – αi = Δαi . z – zi = δ – δi = Δδi
Астрономические каталоги
• В астрономических каталогах содержаться средние координаты звезд, т.е.экваториальные координаты после того, как из них вычтены различные поправки(рефракция, аберрация и др.).
• Каталоги положений составляются на начало определённого года. На основаниикаталогов положений составляются фундаментальные каталоги, в которых, кромеэкваториальных координат, указывается собственное движение звезды, параллаксыи другие данные.
• Первый каталог (более 850 звёзд) был составлен Гиппархом во II веке до н.э.
В настоящее время существует большое множество астрономических каталогов.
Карты и атласы звёздного неба
• «Уранография: описание всего звёздного неба»(«Uranographia: totum caelum stellatum») —атлас звёздного неба Яна Гевелия (JohannesHevelius). Издан в 1690 г. Атлас включает 56 карт. На картах сточностью в одну угловую минуту нанесены1564 звезды по каталогу Гевелия. АтласГевелия достиг точности одного порядка сбумажными картами и атласами нашеговремени.
Дата добавления: 2018-04-15; просмотров: 630; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!