Задачи для самостоятельного решения
Министерство образования Российской Федерации
КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра вычислительной техники и АСУ
МАТЕМАТИЧЕСКАЯ
ЭКОНОМИКА
Методические указания к лабораторным работам для студентов всех форм обучения специальности 351400 - Прикладная информатика в экономике
Краснодар
2004
УДК 681.32
Составитель: доц. Г.В. Бабенко
Математическая экономика. Методические указания к выполнению лабораторных работ для студентов всех форм обучения специальности 321400 – Прикладная информатика в экономике/ Сост.: Г.В. Бабенко; Кубан. гос. технол. ун-т. Каф. вычислительной техники и АСУ. - Краснодар: Изд. КубГТУ, 2003.
Составлены в соответствии с рабочей программой курса “Математическая экономика” для студентов специальности 351400.
Содержат описание лабораторных работ, методические указания к их выполнению и требования к оформлению отчета.
Табл. 4. Библиогр.3 назв.
Печатается по решению Редакционно-издательского совета Кубанского государственного технологического университета
Рецензенты: д-р физ-мат наук, проф. каф. численного анализа Глушков Е. В. (КубГУ)
проф. каф. ВТ и АСУ Максименко Л.А. (КубГТУ)
Содержание
Содержание. 3
Организационно-методические указания. 3
|
|
|
ТЕМА 1. ФИНАНСОВЫЕ ВЫЧИСЛЕНИЯ.. 4
Лабораторная работа №1 Простые проценты. Сложные проценты и наращение по сложной процентной ставке. 4
Лабораторная работа №2 Эффективная процентная ставка. Математическое дисконтирование и банковский учёт. 8
Эффективная процентная ставка. 8
Лабораторная работа №3 Банковский учёт (учёт векселей). Наращение по простой учётной ставке. 10
Лабораторная работа №4 Дисконтирование по сложным годовым учётным ставкам. Дисконтирование по сложной учётной ставке m раз в год. 12
Лабораторная работа №5 Наращение по сложным учётным ставкам. Наращение по сложной учётной ставке m раз в году. 13
Лабораторная работа №6 Наращение процентов и инфляции. Консолидация платежей. Обыкновенная годовая рента. 15
ТЕМА 2. ОЦЕНКА ИНВЕСТИЦИОННЫХ ПРОЕКТОВ.. 17
Лабораторная работа №7 Оценка инвестиционных проектов. Чистая текущая стоимость. 17
Лабораторная работа №8 Показатель доходности. Внутренняя норма окупаемости. 19
ТЕМА 3. ОПТИМИЗАЦИЯ ПОРТФЕЛЯ ЦЕННЫХ БУМАГ. 20
Лабораторная работа №9 Оптимизация портфеля ценных бумаг. 20
ТЕМА 4. АКТУАРНАЯ МАТЕМАТИКА.. 21
Лабораторная работа №10 Актуарная математика. Долгосрочное страхование жизни. 21
|
|
|
Лабораторная работа №11 Оптимизационные задачи. Линейное программирование. Транспортная задача. 21
Список использованной литературы.. 23
Приложение 1. 24
Организационно-методические указания
1 Перед началом лабораторной работы проводится консультация по методике выполнения лабораторных работ по данной дисциплине.
2 Объем каждой лабораторной работы, подготовка и порядок выполнения построены таким образом, чтобы все студенты выполнили работу и сдали отчеты.
3 Студенты готовятся к выполнению очередной работы заблаговременно.
4 Готовясь к лабораторному занятию, студент обязан изучить необходимый теоретический материал, пользуясь настоящими указаниями и рекомендованной литературой, произвести необходимые расчеты, заполнить соответствующую часть отчета и дать ответы на контрольные вопросы.
5 Неподготовленные студенты к выполнению лабораторной работы не допускаются.
6 Студенты, не сдавшие отчет во время занятия, сдают его в назначенное преподавателем время.
7 Студент, не выполнивший лабораторную работу, выполняет ее в согласованное с преподавателем время.
8 Каждая лабораторная работа выполняется студентами самостоятельно. Все студенты предъявляют индивидуальные отчеты. Допускается предъявление отчета в виде электронного документа.
|
|
|
9 Проверка знаний студентов производится преподавателем во время лабораторного занятия и при сдаче отчета.
10 При сдаче отчета студент должен показать знание теоретического материала в объеме, определяемом контрольными вопросами, а также пониманием физической сущности выполняемой работы.
ТЕМА 1. ФИНАНСОВЫЕ ВЫЧИСЛЕНИЯ
Лабораторная работа №1 Простые проценты. Сложные проценты и наращение по сложной процентной ставке.
1 Цель работы.
Научиться решать задачи по простым и сложным процентам, наращению по сложной процентной ставке, используя формулы, а также ППП EXCEL.
2 Краткие теоретические сведения об используемых в лабораторной работе функциях.
БС(ставка;кпер;плт;пс;тип). Возвращает будущую стоимость инвестиции на основе периодических постоянных (равных по величине сумм) платежей и постоянной процентной ставки.
Ставка — это процентная ставка за период.
Кпер — это общее число периодов платежей по аннуитету.
Плт — это выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно плт состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов. Если аргумент опущен, должно быть указано значение аргумента пс.
|
|
|
Пс — это приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей. Если аргумент нз опущен, то он полагается равным 0. В этом случае должно быть указано значение аргумента плт.
Тип — это число 0 или 1, обозначающее, когда должна производиться выплата. Если этот аргумент опущен, то он полагается равным 0.
СТАВКА(кпер;плт;пс;бс;тип;предположение). Возвращает процентную ставку по аннуитету за один период. СТАВКА вычисляется путем итерации и может давать нулевое значение или несколько значений. Если последовательные результаты функции СТАВКА не сходятся с точностью 0,0000001 после 20-ти итераций, то СТАВКА возвращает сообщение об ошибке #ЧИСЛО!.
Кпер — общее число периодов платежей по аннуитету.
Плт — регулярный платеж (один раз в период), величина которого остается постоянной в течение всего срока аннуитета. Обычно плт состоит из платежа основной суммы и платежа процентов, но не включает других сборов или налогов. Если аргумент опущен, должно быть указано значение аргумента бс.
Пс — приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей.
Бс — требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0 (например, бс для займа равно 0).
Тип — число 0 или 1, обозначающее, когда должна производиться выплата.
Предположение — предполагаемая величина ставки.
Если значение предположения опущено, то оно полагается равным 10 процентам.
Если функция СТАВКА не сходится, попробуйте подставить различные значения для предположения. СТАВКА обычно сходится, если величина предположения находится между числами 0 и 1.
БЗРАСПИС(первичное;план). Возвращает будущую стоимость первоначальной основной суммы после применения ряда (плана) ставок сложных процентов. Функция БЗРАСПИС используется для вычисления будущей стоимости инвестиции с переменной процентной ставкой.
Если данная функция недоступна или возвращает ошибку #ИМЯ?, установите и загрузите надстройку «Пакет анализа».
Первичное — это стоимость инвестиции на текущий момент.
План — это массив применяемых процентных ставок.
ПЛТ(ставка;кпер;пс;бс;тип). Возвращает сумму периодического платежа для аннуитета на основе постоянства сумм платежей и постоянства процентной ставки.
Ставка — процентная ставка по ссуде.
Кпер — общее число выплат по ссуде.
Пс — приведенная к текущему моменту стоимость, или общая сумма, которая на текущий момент равноценна ряду будущих платежей, называемая также основной суммой.
Бс — требуемое значение будущей стоимости, или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0 (нулю), т. е. для займа, например, значение бс равно 0.
Тип — число 0 (нуль) или 1, обозначающее, когда должна производиться выплата.
3 Задание.
Задача 1.Кредит на сумму 10 тыс. руб. погашен через 6 месяцев. Какова наращенная (конечная) сумма, если клиент выплачивает банку 30% годовых?
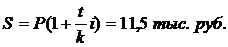
Задача 2.Заёмщик взял банковский кредит в размере 10 тыс. руб. и вернул через 9 месяцев 12 тыс. руб. Определите процентную ставку, под которую был взят кредит.
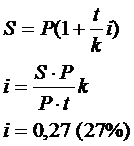
Задача 3. Вкладчик поместил в банк 2 тыс. руб. Какова будет наращенная сумма вклада за 3 месяца, если за первый месяц начисляются проценты в размере 20% годовых, а каждый месяц процентные ставки возрастают на 3%?
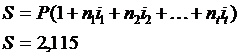
Задачи для самостоятельного решения
Задача 4.Ссуда выдана на срок
а) 5 месяцев
б) 3 месяца
под 10% годовых. Определить процентную ставку на срок ссуды.
Ответ: а)4,17%, б)2,5%
Задача 5.Определить проценты, множитель наращения и сумму накопленного долга, если ссуда равна 100 000 руб., срок долга – 2 месяца, номинальная процентная ставка – 10%.
Ответ: S = 101667 руб.
Задача 6.Определить процентный множитель наращения и сумму накопленного долга при ссуде 7 тыс. руб., сроке долга 2 года, номинальной процентной ставке 10%.
Ответ: S = 8400 руб.
Задача 7.Определить сумму вклада, которую нужно положить в банк сроком на 2 месяца под 10% годовых, чтобы к концу срока получить 10667 руб.
Ответ: P = 100 000 руб.
Задача 8. Определить сумму вклада, которую нужно положить в банк сроком на 2 года под 10% годовых, чтобы к концу срока получить 8400 руб.
Ответ: P = 7000 руб.
Задача 9. Клиент внёс вклад в банк в сумме 1000 руб. сроком на 1 год. Процентная ставка до середины второго квартала составляла 30% годовых, далее до конца третьего квартала – 25%, а с начала четвёртого квартала – снова 30% годовых. Какую сумму получит клиент в конце года?
Ответ: S = 1281,25 руб.
Задача 10.В какую сумму обратится долг, равный 10 тыс. руб., через 5 лет при росте по сложной ставке 10% годовых?
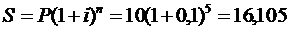
Задача 11.В какую сумму обратится долг, равный 10 тыс. руб. через 5 лет при поквартальном начислении процентов при ставке сложных процентов 10% годовых?
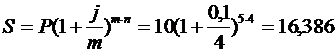
Дата добавления: 2018-04-05; просмотров: 251; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
