Тригонометрическая форма ряда Фурье
Объединяя в (1) комплексно комбинированные составляющие (члены ряда, симметричные относительно центрального ряда S0), можно перейти к ряду Фурье в тригонометрической форме:
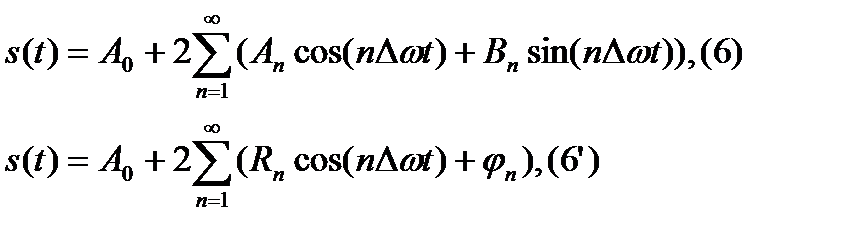
Значение An, Bn вычисляются по формулам (4-5), значения Rn и n - по формулам (3').
Рядом (6) является разложение периодического сигнала s(t) на сумму вещественных элементарных гармонических функций (косинусных и синусных) с весовыми коэффициентами, удвоенные значения которых (т. е. значения 2×An, 2×Bn) не что иное, как амплитуды соответствующих гармонических колебаний с частотами nDw. Совокупность амплитудных значений этих гармоник образует односторонний физически реальный (только для положительных частот nDw) спектр сигнала. Для сигнала на рис. 18, например, он полностью повторяет правую половину приведенных на рисунке спектров с удвоенными значениями амплитуд (за исключением значения Ао на нулевой частоте, которое, как это следует из (6), не удваивается). Но такое графическое отображение спектров используется довольно редко (за исключением чисто технических приложений).
Широкое применение для отображения физически реальных спектров находит формула (6'). Спектр амплитуд косинусных гармоник при таком отображении называется амплитудно-частотным составом сигнала, а спектр фазовых углов гармоник - фазовой характеристикой сигнала. Форма спектров повторяет правую половину соответствующих двусторонних спектров (см. рис. 19) также с удвоенными значениями амплитуд. Для четных сигналов отсчеты фазового спектра могут принимать только значения 0 илиp, для нечетных соответственно ±p/2.
|
|
|
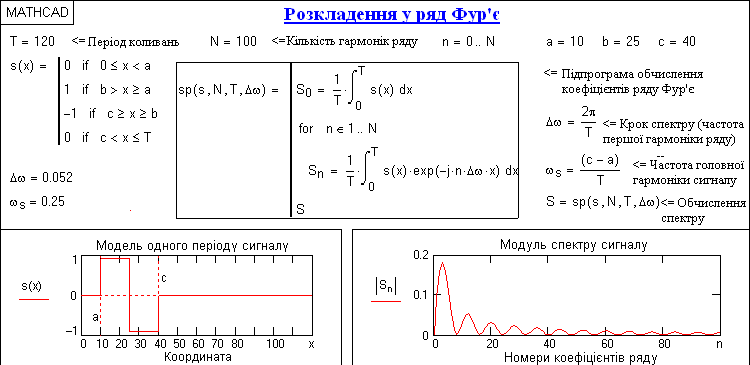
рис. 21 Разложение сигнала в комплексный ряд Фурье
Ряды Фурье произвольных аналоговых периодических сигналов могут содержать бесконечно большое количество членов. Однако одним из важных достоинств преобразования Фурье является то, что при ограничении (усечение) ряда Фурье до любого конечного числа его членов обеспечивается лучшее по средней квадратической погрешности приближение к исходной функции (для этого количества членов).
На рис. 21 показано разложение в комплексный ряд Фурье модельного сигнала, выполненное в среде Mathcad. Модель сигнала задана с тремя разрывами первого рода (скачками). Любой скачок функции содержит все частоты диапазона до бесконечности, в связи с чем ряд Фурье также бесконечен и очень медленно затухает. На рисунке приведены значения только первых 100 членов ряда, при этом график спектра сигнала, как это обычно принято на практике, построенный в виде той, что огибает значений модулей коэффициентов ряда Sn и только по области положительных значений n.
|
|
|
Программа на рис. 22 продолжает программу рис. 21 и показывает реконструкцию сигнала по его спектру при ограничении числа членов ряда Фурье. На верхнем графике рисунка приведен реконструированный сигнал при N = 8 (гармоники первого пика спектра, центр которого соответствует главной гармонике сигнала и члену ряда n = ws/Dw), N = 16 (гармоники двух первых пиков) и N=40 (пять первых пиков спектра). Естественно, что чем больше членов ряда включено в реконструкцию, тем ближе реконструированный сигнал к форме исходного сигнала.
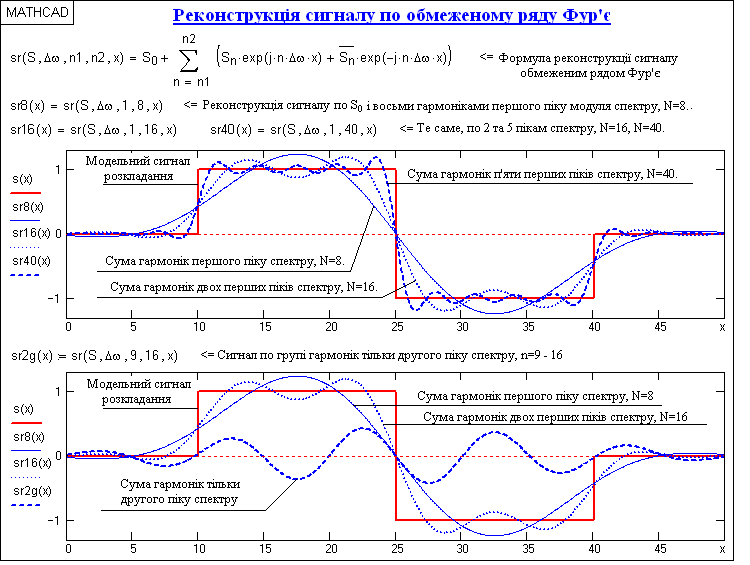
рис. 22. Реконструкция сигнала (продолжение программы на рис. 21)
Принцип последовательного приближения к изначальной формы наглядно видно на нижнем графике рисунка. На нем же можно видеть и причины появления пульсаций на реконструкции скачков функций, которые носят название эффекта Гиббса. При изменении количества суммированных членов ряда эффект Гиббса не исчезает. Не изменяется также относительная амплитуда пульсаций (по отношению к амплитуде скачка) и относительное затухание (по коэффициенту последовательного уменьшения амплитуды пульсаций по отношению к максимальному выбросу), меняется только частота пульсаций, определяемая частотой последних суммированных гармоник.
|
|
|
ИСПОЛЬЗОВАНИЕ ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ(ДПФ)
Дискретная временная область. Дискретная частотная область. Дискретное преобразование Фурье (ДПФ). Обратное ДПФ.
· Цифровой спектральный анализ
· Анализаторы спектра
· Обработка языка
· Обработка изображений
· Распознавание образов
· Проектирование фильтров
· Вычисление импульсной характеристики по частотной
· Вычисление частотной характеристики по импульсной
Быстрое преобразование Фурье (БПФ) - это простой алгоритм для эффективного вычисления дискретного преобразования Фурье (ДПФ)
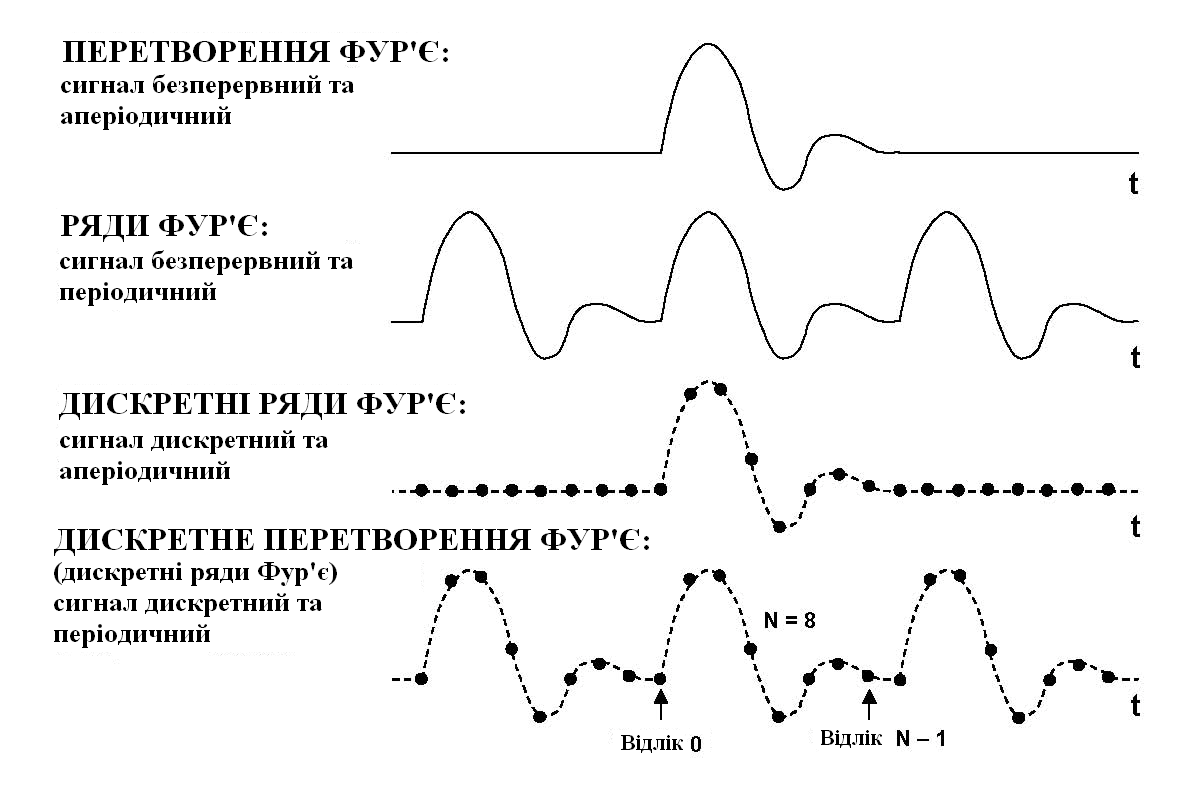
рис. 23 Семейство преобразований Фурье как функция сигнала во временной области
Дискретное преобразование Фурье (ДПФ), которое оперирует дискретной по времени выборкой периодического сигнала во временной области. Для того, чтобы быть представленным в виде суммы синусоид, сигнал должен быть периодическим. Но в качестве набора входных данных для ДПФ доступно только конечное число отсчетов (N). Эту дилемму можно разрешить, если мысленно поместить бесконечное число одинаковых групп отсчетов до и после группы, обрабатывается, образуя, таким образом, математическую (но не реальную) периодичность.
|
|
|
Фундаментальное уравнение для получения N -точечного ДПФ выглядит следующим образом:
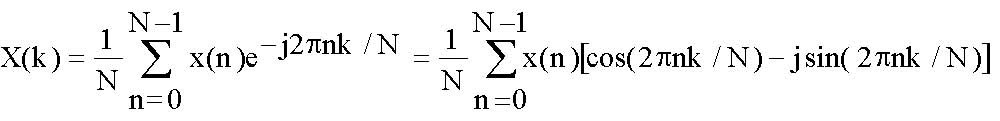
По отношению к этому уравнению следует сделать некоторые терминологические разъяснения. X(k) (прописная буква X) является частотным выходом ДПФ в k-й точке спектра, где k находится в диапазоне от 0 до N-1. N является числом отсчетов при вычислении ДПФ.
Значение x(n) (строчная буква x) представляет собой n-й отсчет во временной области, где n находится в диапазоне от 0 до N-1. В общем уравнении x(n) может быть вещественным или комплексным. Обратите внимание, что косинусоидальные и синусоидальные компоненты в уравнении могут быть выражены в полярных или прямоугольных координатах, связь между которыми определяется по формуле Эйлера:
e jθ = cos θ + j sin θ
Выходной спектр ДПФ X(k) является результатом вычисления свертки между выборкой, состоящей из входных отсчетов во временной области, и набором из N пар гармонических базисных функций (косинус и синус). Концепцию хорошо иллюстрирует рис. 24, на котором представлена вещественная часть первых четырех точек спектра (показаны только косинусоидальные гармонические базисные функции). Подобная процедура используется для вычисления мнимой части спектра на основе синусоидальных функций.
Первая точка X(0) является простой суммой входных отсчетов во временной области, потому что cos(0) = 1. Коэффициент масштабирования 1/N не учитывается, но должно присутствовать в конечном результате. Обратите внимание, что X(0) - это среднее значение отсчетов во временной области, или просто смещение по постоянному току. Вторая точка ReX(1) получена умножением каждого отсчета из временной области на соответствующее значение косинусоиды, что имеет один полный период на интервале N, с последующим суммированием результатов. Третья точка ReX(2) получена умножением каждого отсчета из временной области на соответствующее точку косинусоиды, которая имеет два полные периоды на интервале N, с последующим суммированием результатов. Так же, четвертая точка ReX(3) получена умножением каждого отсчета из временной области на соответствующее точку косинусоиды с тремя полными периодами на интервале N и суммированием результатов. Этот процесс продолжается, пока не будут вычислены все N выходных отсчетов. Подобная процедура, но с использованием синусоид, применяется для вычисления мнимой части частотного спектра. Косинусоиды и синусоиды являются базисными функциями данного преобразования.
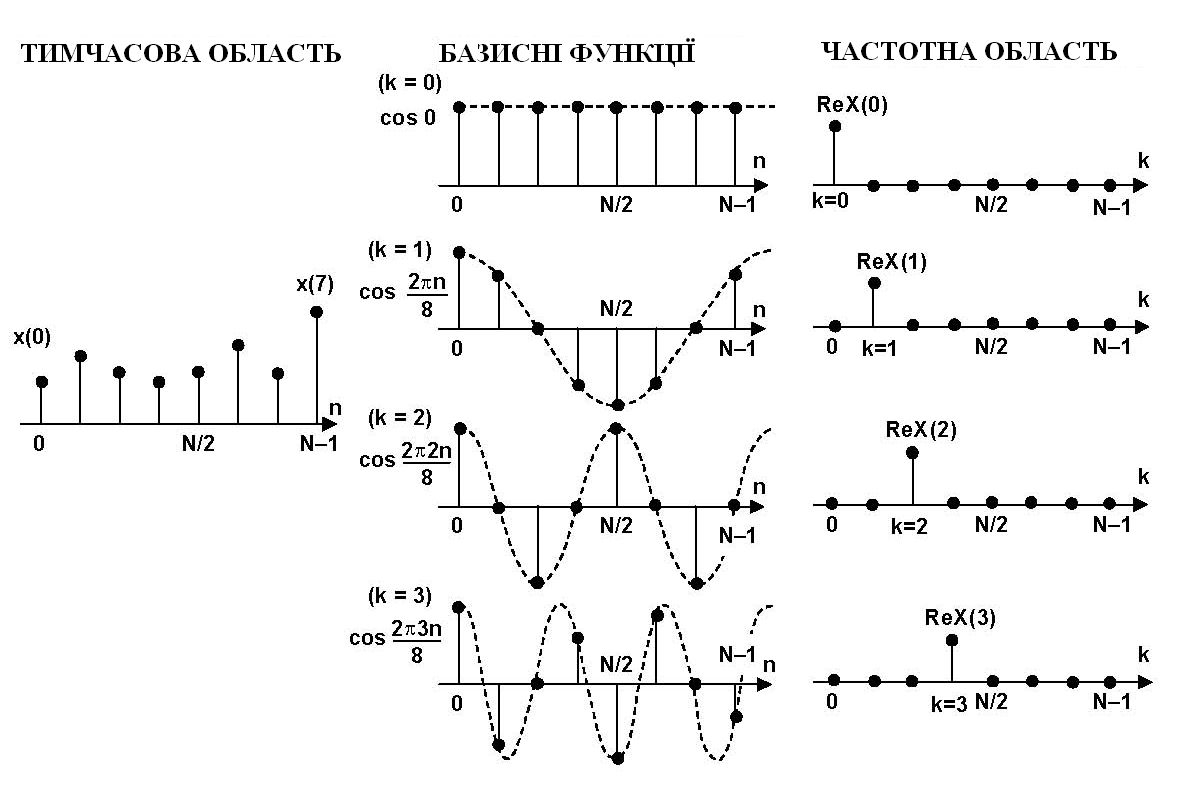
рис. 24 Свертка отсчетов во временной области с базисными функциями при БПФ для N=8
Предположим, что входной сигнал является косинусоидальным, таким, что имеет период N, то есть он содержит один полный период в нашей выборке. Также примем его амплитуду и фазу идентичными первой косинусоидальный базисной функции cos(2πn/8). Выходной спектр содержит одну ненулевую точку ReX(1), а все другие точки ReX(k) являются нулевыми. Предположим, что теперь входная косинусоида сдвинута вправо на 90. Значение свертки между ней и соответствующей базисной косинусоидальной функцией равен нулю. Но алгоритм преобразования предполагает вычисление свертки с базисной функцией sin(2πn/8), необходимое для получения ImX(1). Это показывает, почему необходимо исчислять и вещественные, и мнимые части спектра для определения и амплитуды и фазы частотного спектра.
Обратите внимание, что свертка синусоидальной/косинусоидальной функции любой частоты, отличной от частоты базовой функции, дает нулевое значение и для ReX(1), и для ImX(1).
Подобная процедура применяется при вычислении обратного ДПФ для восстановления отсчетов во временной области x(n) из отсчетов в частотной области X(k). Соответствующее уравнение выглядит следующим образом:
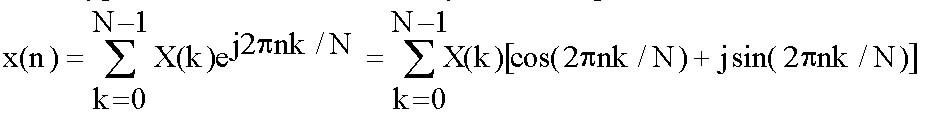
Существуют два основных типа ДПФ: вещественное ДПФ и комплексное ДПФ. Комплексное ДПФ, где и входные, и выходные величины являются комплексными числами. Поскольку входные отсчеты во временной области являются вещественными и не имеют мнимой части, мнимая часть входных отсчетов всегда принимается равной нулю. Выход ДПФ X(k) содержит вещественную и мнимую компоненты, которые могут быть преобразованы на амплитуду и фазу.
Вещественное ДПФ выглядит несколько проще и, в основном, является упрощением комплексного ДПФ. Большинство алгоритмов вычисления быстрого преобразования Фурье (БПФ) составленная с использованием формата комплексного ДПФ, поэтому важно понимать, как работает комплексное ДПФ и как оно соотносится с вещественным ДПФ. В частности, если известны исходные частоты вещественного ДПФ и требуется использовать обратное комплексное ДПФ для вычисления отсчетов во временной области, нужно знать, как разместить исходные точки вещественного ДПФ в формате комплексного ДПФ перед выполнением обратного комплексного ДПФ.
Быстрое преобразование Фурье
Алгоритмы БПФ основаны на том, что при уменьшении длины последовательности решения задачи также уменьшается, но не пропорционально, а гораздо больше.
Пусть сигнал x(n) имеет N отсчетов, причём N=2m.
Разобьем сигнал на две последовательности:
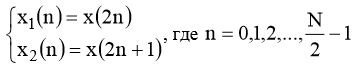
Тогда спектры этих последовательностей будут определены как:
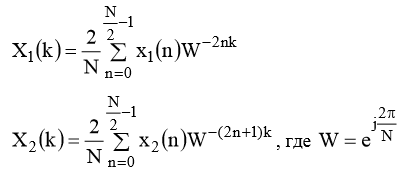
Тогда общий спектр будет выглядеть как:
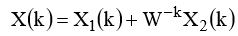
Этот алгоритм называется БПФ с прореживанием по времени. Число отсчетов в этом алгоритме не зря выбрано как степень числа 2. Это позволяет разбивать последовательность к двухточечной преобразования Фурье:
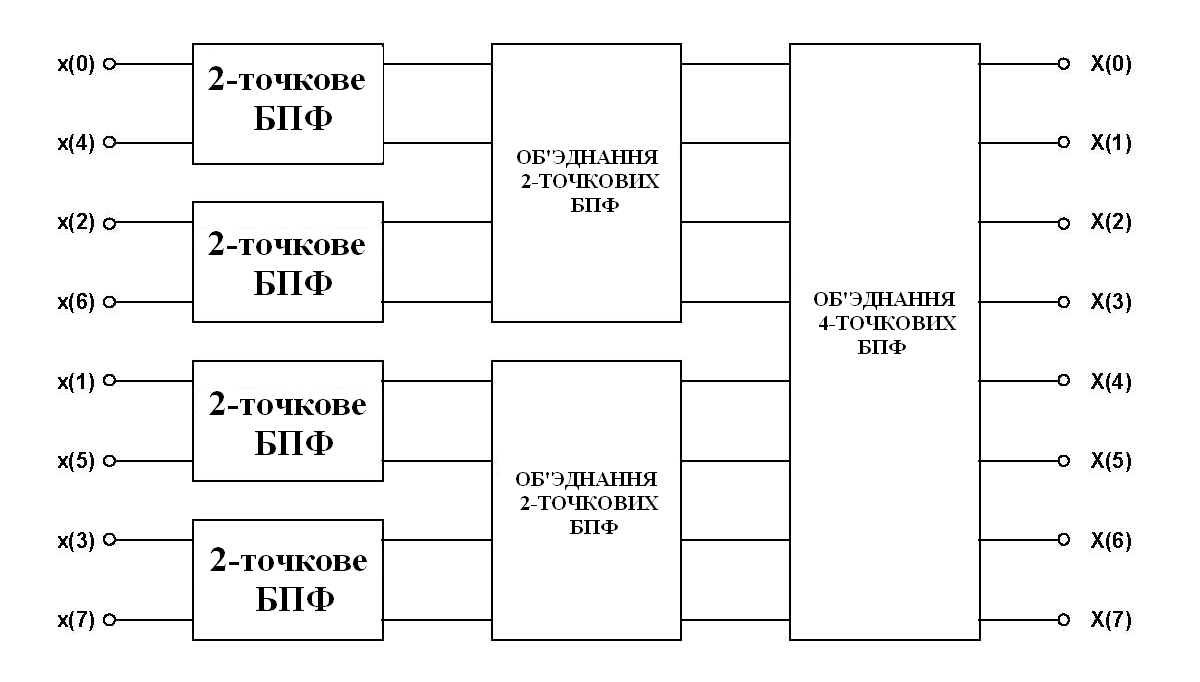
рис. 25 Вычисления 8-точечного БПФ в трех каскадах с использованием прореживания по времени
Пример вычисления БПФ для 8 отсчетов Дискретное преобразование Фурье:
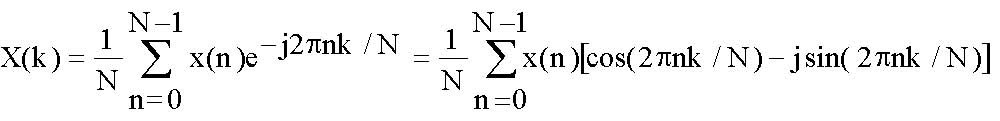
ФормулаЭйлера: e jθ= cos θ + j sin θ
Обратная ДПФ:
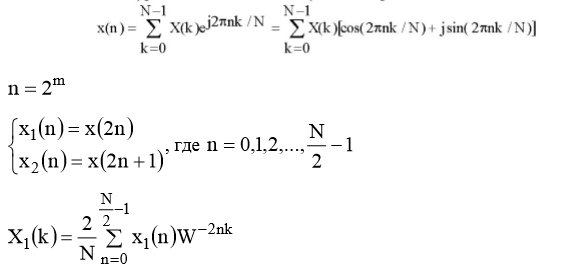
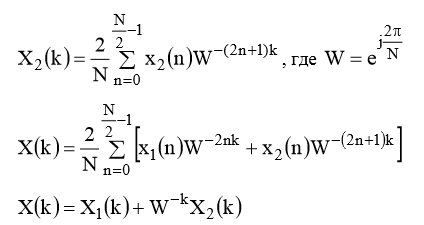
Дата добавления: 2018-04-05; просмотров: 924; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
