Дискретное косинусное преобразование
Дискретное косинусное преобразование (ДКП) является преобразованием массива пикселей в массив значений пространственной частоты. Это преобразование является обратным с точностью до ошибок округления. Оно позволяет переходить от пространственного представления изображения к его спектральному представлению и обратно. Изображение, представленное матрицей размера NxN, может быть представлено с помощью коэффициентов двумерного косинусного преобразования следующим образом:
Само ДКП выглядит следующим образом:
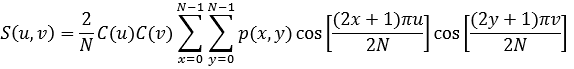
В алгоритме JPEG используют ДКП исходного изображения блоками размера 8х8 пикселей. Размер выбран так, чтобы не сильно увеличивать вычислительную сложность алгоритма и при этом иметь минимум визуальной потери качества изображения. ДКП для удобства осуществляется последовательно, в несколько этапов. Сначала создается ДКП матрица 8х8, использующая формулу:
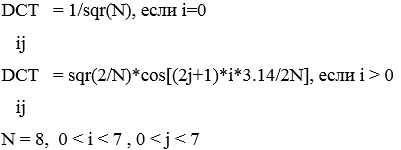
В результате имеем:
Начальное изображение поддается смещению уровня яркости так, чтобы значения яркости были симметричны относительно 0. Для изображений, содержащих 256 цветов, данная процедура совершается путем отнимания от значений яркости пикселей 128.
Например, нам нужно сжать следующий фрагмент изображения:
Вот формула, по которой приводится ДКП: RES * IMG * DCT
Для начала надо рассчитать промежуточную матрицу: TMP = IMG * DCT
Потом умножаем ее на ДКП матрицу: RES = TMP * DCT
|
|
|
Этап квантования
На этом этапе мы вычисляем матрицу квантования, используя этот псевдо код:
for i:=0 to 8 do
for j:=0 to 8 do
Q[i,j] = 1+((1+i+j)*q);
Где q – коэффициент качества, от него зависит степень потери качества сжатого изображения. Для q = 2 имеем матрицу квантования:
Теперь надо каждое число в матрице квантования разделить на число в соответствующей позиции в матрице RES, в результате получим:
Как видим, тут достаточно много нулей, мы получаем наиболее длинную последовательность нулей, если будем использовать алгоритм зигзагообразного обхода блока:
Таблица 13. Зигзагообразный обход блока
| 1 | 2 | 6 | 7 | 15 | 16 | 28 | 29 |
| 3 | 5 | 8 | 14 | 17 | 27 | 30 | 43 |
| 4 | 9 | 13 | 18 | 26 | 31 | 42 | 44 |
| 10 | 12 | 19 | 25 | 32 | 41 | 45 | 54 |
| 11 | 20 | 24 | 33 | 40 | 46 | 53 | 55 |
| 21 | 23 | 34 | 39 | 47 | 52 | 56 | 61 |
| 22 | 35 | 38 | 48 | 51 | 57 | 60 | 62 |
| 36 | 37 | 49 | 50 | 58 | 59 | 63 | 64 |
Итак, мы получили последовательность:
30 0 -7 -11 8 0 0 1 6 -5 -7 -3 0 1 0 0 0 1 0 -3 -4 -1 4 2 0 0 0 0 0 0 0 0 0 0 0 -3 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Этап вторичного сжатия
Наиболее распространенным методом вторичного сжатия является метод Хаффмана и его разновидности.
Восстановление изображения, сжатого с помощью алгоритма JPEG.
|
|
|
При распаковке изображения выполняется обратная последовательность шагов:
1. Выполняется декодирование данных, полученных в результате вторичного сжатия. На этом этапе восстанавливается матрица квантованных коэффициентов.
2. Выполняется деквантование матрицы, в результате чего получается матрица близкая к исходной матрице, полученной после косинусного преобразования. Она близка, но не точна, за счет округления на этапах квантования и деквантования.
3. Выполняется обратное дискретное косинусное преобразование, которое восстанавливает первоначальный массив пикселей.
JPEG без потерь
Это самый простой режим работы без потери данных, основанный на прогнозируемой модели. Как правило, этот метод позволяет достичь коэффициента
сжатия около 2:1, что значительно меньше, чем коэффициенты, которые могут быть достигнуты в методах, основанных на ДКП.
Одно из отличий: обрабатывается все изображение, а не блок размера 8х8. При сканировании изображения каждое значение пикселя заменяется значением: Результат = Пиксель - Прогноз
Здесь «Прогноз» – значение, основанное на значениях некоторых отсканированных ранее соседних пикселях. Смысл заключается в следующем: как правило, значение пикселя на реальном изображении близкое к значениям соседних точек. Поэтому прогноз, основанный на значениях соседних пикселей, должно быть близким к фактическому значению или совпадать с фактическим значением. Если преобразовать матрицу пикселей в разностную матрицу, основанную на прогнозах, многие значения окажутся равными нулю, а остальные будут небольшие. Преобразованное изображение должно упаковываться компактнее. Для упаковки, как правило, применяют метод Хеффмана.
|
|
|
Схема JPEG позволяет использовать прогноз, основанный на значениях некоторых или всех пикселей, смежных с текущим, но встреченных ранее в процессе сканирования слева направо или сверху вниз. Для каждого пикселя, кроме пикселей левого столбца и верхнего ряда, у которых есть только один предыдущий пиксель.
рис. 13 Размещение пикселей
Возможны следующие режимы кодирования:
табл. 14 Режимы кодирования
| Режимкодирования | Прогноз |
| 0 | Отсуствует |
| 1 | A |
| 2 | B |
| 3 | C |
| 4 | A+B+C |
| 5 | A+((B-C)/2) |
| 6 | B+((A-C)/2) |
| 7 | (A+B)/2 |
Как видно из рисунка и таблицы, алгоритм сжатия без потерь может быть настроен для любой комбинации предыдущих точек. В режимах с 1 по 3 используются одномерные прогнозы. В режимах с 4 по 7 – двумерные. Какие из них задействуются, зависит от реализации и положения пикселя, что кодируется.
|
|
|
В любом случае задействуются следующие правила:
1. Значение прогноза для левого верхнего пикселя равно 2^(P - 1), где P – глубина цвета исходного изображения.
2. Для других точек верхнего ряда прогноз основывается на значении левого соседа (режим 1).
3. Для других точек левого столбца прогноз основывается на значении соседа сверху (режим 3).
Основы сжатия изображений
Основные задачи, решаемые при цифровой обработке изображений: Пример кодирования JPEG
DCT-матрица для блока 8х8 пикселей
Начальное изображение:
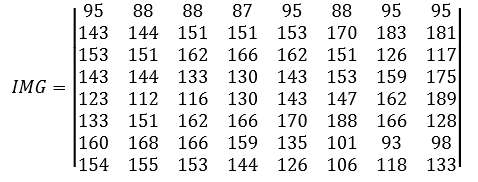
Изображение после смещения яркости:
Матрица IMG * DCT
Результирующая матрица ДКП:
Матрица квантования для q = 2:
Результат квантования:
Результат обхода:
30 0 -7 -11 8 0 0 1 6 -5 -7 -3 0 1 0 0 0 1 0 -3 -4 -1 4 2 0 0 0 0 0 0 0 0 0 0 0 -3 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Обратное ДКП:
Принцип превращения матрицы изображения в JPEGбез потерь:
Результат = Пиксель – Прогноз
ОБРАБОТКА ЗВУКОВЫХ СИГНАЛОВ
Звуковая информация представляется в цифровом виде в двух принципиально разных формах – WAVE и MIDI.
WAVE – форма используется для цифровых аудиодисков, а MIDI - в электронных музыкальных инструментах.
WAVE-форма звука
WAVE-форма звука получается при оцифровке, или дискретизации, непрерывной звуковой волны (англ. wave – волна), точнее, аналогового аудиосигнала. При оцифровке специальное устройство – аналого-цифровой преобразователь (АЦП) – измеряет амплитуду волны через равные промежутки времени со скоростью несколько тысяч измерений в секунду и запоминает в Wave-файл измеренные значения. Они называются выборками (по англ. sample, откуда еще одно название дискретизации – сэмплинг). Обратное преобразование WAVE-формы звука в аналоговый сигнал осуществляется цифро-аналоговым преобразователем (ЦАП).
На рис. 14 представлена фонограмма первых 10 секунд 40-й симфонии Моцарта, содержащий 2 205 000 выборок. Если на вашем компьютере установлена звуковая плата, вы сможете ее прослушать, щелкнув мышью на картинке. На рис. 15 показан фрагмент записи, содержащий только 50 выборок, начиная с места, отмеченного на рис. 14 вертикальной чертой.
рис. 14 Фонограмма первых 10 секунд 40-ой симфонии Моцарта
рис. 14 Фонограмма симфонии Моцарта
WAVE-форма цифрового звука характеризуется пятью параметрами:
· Частотой дискретизации,
· Разрядностью выборок,
· Количеством каналов или звуковых дорожек,
· Алгоритмом компрессии/декомпрессии – кодеком,
· Форматом хранения.
Чистота дискретизации
Под дискретизацией сигналов понимают преобразование функций непрерывных переменных в функции дискретных переменных, по которым исходные непрерывные функции могут быть восстановлены с заданной точностью. Каждое значение функции дискретной переменной называется отсчетом. Очень часто роль отсчетов выполняют квантованные значения функций в дискретной шкале координат.
Под квантованием понимают преобразование непрерывной по значениям величины в величину с дискретной шкалой значений из конечного множества разрешенных, которые называют уровнями квантования. Сущность квантования состоит в округлении мгновенных значений входной функции до ближайших значений уровней квантования. Если уровни квантования нумерованы, то результатом преобразования является число, которое может быть выражено в любой числовой системе. Количество выборок в секунду называется частотой дискретизации и измеряется в герцах и килогерцах (1 кГц=1000 выборок в сек.). При определении количества выборок следует учитывать, что чем меньше интервал между отсчетами (выборками) dt, тем больше будет частота дискретизации и сигнал будет описан точнее. С другой стороны, для обработки такого сигнала будет нужен больший объем памяти, большие ресурсы процессора, больше времени. Поэтому для определения оптимальной частоты дискретизации пользуются теоремой Котельникова (Котельникова - Найквиста).
Теорема гласит: Если непрерывный сигнал x(t), который существует на всей числовой оси и имеет ограниченный спектр [- w, w] заменить отсчетами с минимальным шагом dt=pi/Wm=1/2Fm, то по этой множественном числе отсчетов возможно безошибочное восстановление сигнала x(t).
То есть теоретически, для правильного восстановления аналогового сигнала по его цифровой записи достаточно, чтобы частота дискретизации более чем в два раза превосходила максимальную частоту звука.
рис. 16 Определение оптимальной частоты дискретизации
Таким образом, для качественного воспроизведения самого звука 20 кГц, что возможно услышать, нужна частота дискретизации не менее 40 кГц. Стандарт CD - DA цифровых аудиодисков требует частоты дискретизации 44,1 кГц (так называемое CD-качество). Используются также частоты 22,05 (радио - качество) и 11,025 и 8 кГц (телефонное качество), что во многих случаях дают удовлетворительные результаты (например, для записи речи). Звук является сложным сигналом, но, как и любой другой сигнал, он может быть представлен с помощью ряда Фурье в виде суммы постоянных составляющих, а также синусов и косинусов, то есть гармонических сигналов (или гармоник).
Но при оцифровке звука дискретизируются и высокочастотные гармоники с частотой, превышающей половину частоты дискретизации (это высокочастотный, неслышимый шум). При этом появляются новые нежелательные гармоники из слышимого диапазона (низкочастотный шум, см. рис. 17).
рис. 17 Появление низкочастотных помех
Поэтому для получения качественного цифрового звука процесс дискретизации строится по следующей схеме:
• частичное подавление высокочастотных помех в аналоговом сигнале с помощью аналогового фильтра;
• оверсэмплинг – дискретизация с частотой, что значительно превышает требуемую (при этом шум, что образуется, все еще лежит в нечутному диапазоне);
• подавление высокочастотного шума в цифровом звуке с помощью цифрового фильтра;
• преобразование до требуемой частоты дискретизации.
Оверсэмплинг применяется и при обратном преобразовании к аналоговому сигналу. При этом используются различные методы линейной и нелинейной интерполяции.
Разрядность выборки
Измеренная амплитуда (выборка) превратится в целое число с некоторой погрешностью, которая определяется разрядностью этого числа. Это преобразование в числа с заданной разрядностью называется квантованием. Погрешность при квантовании вносит шум тем больше, чем меньше разрядность. Теоретически, при n-разрядном квантовании отношение сигнал/шум (динамический диапазон) будет 6n дБ. Таким образом, при 8-разрядном оцифровке динамический диапазон 48 дБ (качество УКВ-радио, достаточная для языка), а при 16-разрядной оцифровке он равен 96 дБ и практически покрывает весь нормально слышимый диапазон. Другими словами, при 8-разрядном кодировании различаются 256 уровней громкости, а при 16-разрядном – 65536, что дает более точную запись. На CD-DA применяется 16-разрядное квантование. Звуковые платы компьютеров обычно используют 8 и 16-разрядное квантование. Применение оверсэмплинга в АЦП и ЦАП позволяет значительно уменьшить шум, который добавляется при квантовании.
Каналы
Обычные звуковые платы позволяют использовать 1 или 2 звуковых канала (дорожки) WAVE-звука – "моно" и "стерео". Оба канала обрабатываются отдельно по одним и тем же алгоритмам, хоть и одновременно. Поэтому нет принципиальных ограничений на число каналов. Увеличение количества каналов ведет к пропорциональному увеличению объема памяти, которую занимает звуковая информация.
Основные методы обработки звука: сжатие, аналоговая фильтрация, цифровая фильтрация.
Компрессия звука
Обозначим
• W – объем памяти в байтах для хранения 1 секунды звука в WAVE-форме,
• w – скорость потока звуковых данных в WAVE-форме в бит/сек,
• H – частоту дискретизации (число выборок в секунду),
• B– разрядность квантования (число разрядов на выборку),
• C – количество каналов.
Тогда очевидно, что w = H*B*C, если B кратно 8, W = w/8. Итак,
• скорость потока данных CD-качества (H=44100, B=16, C=2) составляет 1 411 200 бит/сек или 1378,125 Кбит/сек (такая скорость обеспечивается только CD
-дисководом с не менее, чем 2-кратной скоростью),
• 1 час звука с качеством CD-DA нуждается 605,6 Мбайт (поэтому на аудиодиске помещается около 70 минут несжатого звука),
• скорость потока данных телефонного качества (H=8000, B=8, C=1) составляет 64000 бит/сек или 62,5 Кбит/сек (такая скорость обеспечивается далеко не каждым модемом, поэтому такой звук не может использоваться в Интернет - телефонии).
С целью уменьшения объема и потока звуковых данных в WAVE-форме используются различные специальные алгоритмы компрессии/декомпрессии (кодеки), поскольку обычные алгоритмы сжатия информации здесь не дают эффекта. Сжатие аудиоданных возможно лишь с некоторой потерей информации, но учет психофизиологических особенностей восприятия звука (например, не все частоты в слышимом диапазоне существенные для восприятия), позволяет в ряде случаев сделать эти потери практически незаметны. Однако следует учитывать очень высокую чувствительность человеческого слухового аппарата, особенно временных характеристик звука. Наиболее известными являются следующие кодеки, которые используются в мультимедиа под Windows:
• PCM (PulseCodeModulation) – импульсно-кодовая модуляция (ИКМ) – сжатие может достигаться только за счет выбора меньших значений величин H, B и C (фактически, это несжатая звук); квантование происходит по равномерной шкале из 2B значений;
• DPCM (DifferentialPCM) – дифференциальная ИКМ (ДИКМ) – выборка представляет разницу от предыдущей, что требует меньше B битов; сжимает в несколько раз;
• ADPCM (AdaptiveDPCM) – адаптивная ДИКМ (АДИКМ) – то же, что ДИКМ, только квантование происходит не по равномерной шкале, а с учетом динамики изменений амплитуды; сжимает в несколько раз;
• MPEG (MotionPictureExpertsGroup) – стандарты Группы экспертов в области кино; для сжатия звуковой информации используются стандарты MP2 и MP3; применяется психоакустическая компрессия, при которой удаляются звуки, не воспринимаемые человеческим ухом; сжимает в несколько десятков раз при достаточно высоком качестве;
• RealAudio – метод, разработанный фирмой RealNetworks, сжимает в несколько десятков раз, но с невысоким качеством; используется в Интернете для проигрывания звуковых файлов в реальном времени.
Для цифровой телефонии используются, как правило, другие кодеки.
Спектральная (частотная) форма представления сигналов использует разложение сигнальных функций на периодические составляющие.
Периодичность гармонических колебаний исследовал еще в VI веке до нашей эры Пифагор и даже распространил ее на описание гармонического движения небесных тел. Термин «spectrum» («спектр») впервые применил И. Ньютон в 1571 году при описании разложения солнечного света, пропущенного через стеклянную призму, на многоцветную полосу. Он же дал и первое математическое трактовку периодичности волновых движений. В 18-м веке решениями волновых уравнений (в приложении к струнам) занимались Даниил Бернулли и Леонард Эйлер. По сути, уже Бернулли и Эйлера показали, что произвольные периодические функции представляют собой суммы простейших гармонических функций – синусов и косинусов кратных частот. Эти суммы получили название рядов Фурье, после того, как в 1807 году французский инженер Жан Батист Фурье обосновал метод вычисления коэффициентов тригонометрического ряда, которым можно показать с абсолютной точностью (при бесконечном количестве членов ряда) или аппроксимировать с заданной точностью (при ограниченном количестве членов ряда) любую периодическую функцию, определенную на интервале одного периода T = b - a, и что удовлетворяет условиям Дирехле (ограниченная, кусочно-непрерывная, с конечным числом разрывов 1-го рода).
А если быть точнее:
На первых этапах своего развития данное направление разложения функций, получившее название гармонического анализа, имело более теоретический характер и использовалось, в основном, в естественных науках для выявления и изучения периодичности и состава периодических составляющих (в том числе скрытых) в различных явлениях и процессах (активность солнца, девиация магнитного поля Земли, метеорологические наблюдения, высота приливов в гаванях и тому подобное). Положение резко изменилось с появлением электротехнических и радиотехнических отраслей науки и техники и развитием радиосвязи, где гармонический состав сигналов приобрел конкретного физического смысла, а математический аппарат спектрального преобразования функций стал основным инструментом анализа и синтеза сигналов и систем. Сегодня спектральный анализ является одним из основных методов обработки экспериментальных данных во многих отраслях науки и техники.
В качестве базисных функций разложения сигналов, в общем случае, принимаются комплексные экспоненциальные функции exp(jft), от которых с использованием формул Эйлера можно перейти к вещественным синус – косинусных функций. Термин «частотная» обязан происхождением обратная переменной f = 1/|t| временного представления сигналов и функций. Понятие частотного преобразования не следует связывать только с временными аргументами, поскольку математический аппарат преобразования не зависит от физического смысла независимых переменных. Так, например, при переменной "х", как единице длины, значение f будет пространственной частотой с размерностью 1/|х – число периодических изменений сигнала на единице длины.
В математическом аппарате частотного анализа удобно использовать угловую частоту ω = 2πf. Для процессов с другими независимыми переменными в технической литературе вместо индекса частоты f часто используется индекс v, а для угловой частоты индекс k = 2πv, который называют волновым числом.
РАЗЛОЖЕНИЕ СИГНАЛОВ ПО ГАРМОНИЧЕСКИМ ФУНКЦИЯМ
Понятие собственных функций
Удобство использования частотного представления сигналов заключается в том, что гармонические функции являются собственными функциями операций переноса, интегрирования, дифференцирования и других линейных операций, инвариантных по координатам. Предположим, что начальная функция является линейной комбинацией функций синуса и косинуса:
𝑠(𝑥) = 𝐴sin(𝑥) + 𝐵cos(𝑥)
Осуществим произвольный сдвиг функций с аргументом на величину h. При этом получаем:
𝑠(𝑥 + ℎ) = 𝐶sin(𝑥) + 𝐷cos(𝑥)
𝐶 = 𝐴cos(ℎ) − 𝐵sin(ℎ)
𝐷 = 𝐴sin(ℎ) + 𝐵cos(ℎ)
где коэффициенты C и D, как и в начальном выражении коэффициенты А и В, не зависят от аргумента, при этом C2+D2=А2+В2. Таким образом, при произвольном переносе функции с аргументом (а равно и при интегрировании, дифференцировании и других линейных преобразованиях) любую линейную комбинацию синуса и косинуса можно представить линейной комбинацией этих же функций.
Экспоненциальный комплексный запись гармонических функций делает это свойство еще нагляднее. Для произвольной гармонической функции имеем:
cos(𝜔𝑡 − 𝜑) = 𝐴cos(𝜔𝑡) + 𝐵sin(𝜔𝑡)
де𝐴=cos(𝜑),𝐵=sin(𝜑),𝜑–начальный фазовый угол колебания при t = 0. Переходя к комплексной записи данной функции с использованием тождеств Эйлера:
Получаем: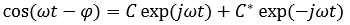 
Где, 
- величина, комплексно сопряженная с С. Применяя в качестве гармонической составляющей разложения сигнала функцию ехр(jωt), можно рассматривать вторую функцию ехр(–jωt), комплексно сопряженную с первой, как такую же составляющую, но с отрицательной частотой. Естественно, что отрицательная частота является чисто математической абстракцией, но нужно помнить, что пара таких комплексно сопряженных составляющих в сумме всегда дает вещественную функцию.
Экспоненциальные функции также являются собственными функциями линейных операций. Для операции переноса с использованием экспоненциальных функций:
, где 
- собственное значение операции переноса, независимое от переменной.
Для операции дифференцирования:
Для операции интегрирования:
В общей форме для любых операций преобразования:
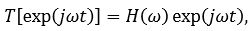где T[.] – произвольный линейный оператор, Н(ω) – собственное значение операции, независимо от аргумента.
У специалистов-практиков существует предубеждение против использования комплексных функций с их мнимыми частотами. Поэтому в дальнейшем будем использовать и вещественные функции, и их комплексные аналоги, по крайней мере, до тех пор, пока простота и удобство использования последних не станет очевидной.
Ряды Фурье
Разложению в ряды Фурье подвергаются периодические сигналы. Периодическую функцию любой формы, заданную на интервале одного периода Т = b - a ту, что удовлетворяет на этом интервале условиям Дирехле (ограниченная, кусочно - непрерывная, с конечным числом разрывов 1-го рода), можно представить в виде ряда Фурье:
,
где весовые коэффициенты Snряда определяются по формуле:
Ряд Фурье является ансамблем комплексных экспонент exp(jnΔωt) с частотами, образующими арифметическую прогрессию. Функцию весовых коэффициентов S(nΔω) принято называть комплексным спектром периодического сигнала или Фурье-образом функции s(t). Спектр периодического сигнала является дискретной функцией, поскольку он определен только для целых значений n с шагом по частоте, обратным к периоду: Δω = 2π/Т (илиΔf = 1/T). Первую частотную составляющую спектра при n = 1, равную ω1 = 1*Δω = 2π/T (или f1 = 1/T), называют основной частотой сигнала (первой гармоникой), другие частоты дискретного спектра n1 при n>1 называют гармониками сигнала. Значение S(nω1) по положительным и отрицательным значениях n являются комплексно сопряженными.
С чисто математических позиций множество функций exp(jnΔωt) образует бесконечномерный базис линейного пространства L2[a, b] ортогональные синус-косинусных функций, а коэффициенты Sn по (2) являются проекциями сигнала s(t) на эти базисные функции. Соответственно, сигнал s(t) в форме ряда Фурье (1) - это бесконечномерный вектор в пространстве L2[a, b].
Подынтегральную функцию экспоненты в выражении (2) с использованием тождества Эйлера exp(-jωt)=cos(ωt) – j*sin(ωt) можно разложить на косинусную и синусную составляющие и выразить комплексный спектр в виде действительной и мнимой частей:
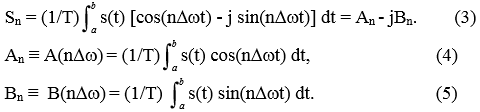
На рис. 4.1.1 приведен пример периодического сигнала (прямоугольный импульс на интервале (1-3.3), повторяющийся с периодом Т=40) и форма действительной и мнимой части его спектра. Обратим внимание, что действительная часть спектра является четным относительно нуля функцией A(nDw) = A(- nDw), поскольку при вычислении значений A(nDw) по формуле (4) используется парная косинусна функция cos(nDwt) = cos(-nDwt). Мнимая часть спектра является нечетной функцией B(nDw) = -B(-nDw), поскольку для ее вычисления по (5) используется нечетное синусная функция sin(nDwt) = - sin(-nDwt).
рис. 18 Сигнал и его комплексный спектр.
Комплексные числа дискретной функции (3) могут быть представлены в виде модулей и аргументов комплексной экспоненты, что дает следующую форму записи комплексного спектра:
Sn = Rn exp(jjn), (4.1.3')
Rn2≡ R2(nDw) = A2(nDw)+B2(nDw),
jn ≡ j (nDw) = arctg(-B(nDw)/A(nDw)).
рис. 19 Модуль и аргумент спектра.
Модуль спектра R(n)wD называют двусторонним спектром амплитуд, а аргумент спектра (последовательность фазовых углов (jn))wD - двусторонним спектром фаз. Спектр амплитуд всегда является четной функцией: R(n) =wDR(- n),wD а спектр фаз нечетную(j: n(-j) = -wDn).wD Пример спектра в амплитудном и фазовом представлении для сигнала, показанного на рис. 18, приведен на рис. 19. При рассмотрении спектра фаз следует учитывать периодичность 2p угловой частоты (при уменьшении фазового значения до величины меньше p- происходит сброс значения - 2p).
рис. 20 Ортогональность функций
Если функция s(t) является четной, то все значения B(nwD) по (5) равны нулю, поскольку четные функции ортогональные синусным гармоникам и подынтегральное произведение s(t) - sin(nwDt) дает нулевой интеграл. Следовательно, спектр функции будет представлен только вещественными коэффициентами. Наоборот, при нечетности функции s(t) обнуляются все значения коэффициентов А(нечетные функции ортогональным косинусным гармоникам) и спектр является чисто мнимым. Этот фактор не зависит от выбора границ задачи периода функции на числовой оси. На рис. 20(А) можно наглядно видеть ортогональность первой гармоники синуса и четной функции, а на рис. 20(В) соответственно косинуса и нечетной функции в пределах одного периода. Учитывая кратность частот следующих гармоник первой гармонике спектра, ортогональность сохраняется для всех гармоник ряда Фурье.
При n = 0 имеем Во = 0, и получаем постоянную составляющую сигнала:
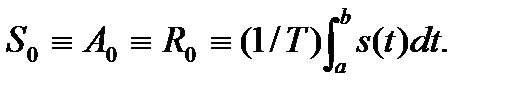
Дата добавления: 2018-04-05; просмотров: 6655; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!