Особенности и нежелательные эффекты

Стр 1 из 6Следующая ⇒

Лабораторная работа 3

СПЕКТРАЛЬНЫЙ АНАЛИЗ СИГНАЛОВ

(4 часа)

Цель работы:познакомиться с основами спектрального анализа цифровых сигналов.

Задачи работы:

1. познакомиться с теоретическими основами спектрального анализа;

2. изучить алгоритмы оценки спектральной плотности мощности (СПМ);

3. сравнить методы оценки СПМ;

4. закрепить полученные знания на практических примерах в пакете MATLAB.

Оглавление

1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.. 2

1.1. Спектральный анализ сигналов. Введение. 2

1.2. Принципы оценки спектра. 4

1.3. Традиционные методы.. 6

1.3.1. Особенности и нежелательные эффекты.. 6

1.3.2. Взвешивание. Свойства весовых функций. 10

1.3.3. Метод и свойства периодограмм. 13

1.3.4. Методы модифицированных периодограмм. 15

1.3.5. Сравнение традиционных методов оценки СПМ.. 17

1.4. Современные параметрические методы оценки. 18

1.4.1. Общие сведения. 18

1.4.2. Авторегрессионная оценка спектра. 18

1.4.3. Авторегрессионная модель и авторегрессионный фильтр. 19

1.4.4. Спектральная плотность мощности авторегрессионного ряда. 20

1.4.5. Порядок модели. 21

1.5. Сравнение методов оценки. 21

1.6. Описание некоторых команд MATLAB.. 22

1.6.1. Функции окон. 22

1.6.2. Расчет периодограммы.. 22

1.6.3. Реализация метода Уэлша. 24

1.6.4. Авторегрессионные методы.. 26

2. ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ.. 28

3. КОНТРОЛЬНЫЕ ВОПРОСЫ.. 29

4. БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 30

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Спектральный анализ сигналов. Введение

Преобразование данных из временной области в частотную было описано в предыдущей лабораторной работе. В данной работе развиваются принципы и навыки оценки и анализа спектра в частотной области. Вообще, графики зависимости амплитуд или фаз гармоник от частоты часто более удачно представляют данные или сигналы, особенно если сигналы имеют случайную природу. Выбирая согласно некоторому критерию определенные гармоники и отбрасывая другие, можно существенно сжать данные. Спектральный анализ оказался полезным в таких областях, как изучение сигналов техники связи или смоделированных откликов человеческой электроэнцефалограммы (ЭЭГ) при диагностике болезней головного мозга, других биологических сигналов, метеорологических данных, в управлении технологическим процессом и измерении спектра шума при разработке оптимальных линейных фильтров.

Существующие методы оценки спектра можно разделить на параметрические и непараметрические. Непараметрические методы включают периодограммы, модифицированные периодограммы Барлета (Barlett) и Уэлша (Welsh) и метод Блэкмена-Тьюки (Blackman-Tukey). Плюс: все эти методы можно реализовать с использованием быстрого преобразования Фурье; минус: если данные представляются короткими словами разрешение по частоте ограничено. Кроме того, чтобы получить значимые результаты, следует быть очень аккуратными. С другой стороны, параметрические методы не только вычислительно эффективнее, но и могут давать большее разрешение. Впрочем: перед оценкой спектра процесса нужно вначале построить достаточно точную модель этого процесса. Если выбран параметрический подход, чаще всего спектр выводится из параметров авторегрессионной модели сигнала.

При выполнении непараметрического спектрального анализа нужно обойти множество подводных камней. Связанные с этим темы наложения, гребешковых искажений, конечной длины данных, просачивания спектральных составляющих и размывания спектра очень важны, и мы подробнее обсудим эти моменты далее.

Отрицательное воздействие просачивания спектральных составляющих и размывания можно минимизировать, ограничив данные посредством подходящей весовой функции. Дискретные данные по одной выборке множатся на дискретные значения выбранной весовой функции. Основными свойствами весовой функции являются ширина полосы шумового (или прямоугольного) эквивалента, коэффициент расширения спектра, потери (времени) при обработке данных в наихудшем случае и полоса минимального разрешения. В разделе по корреляции перекрывающихся областей показано, что усреднение спектра из нескольких взвешенных фрагментов данных вместо непосредственного вычисления спектра всех взвешенных данных дает значительно лучшую оценку спектра.

Суждения о качестве спектральных оценок основаны на теории оценок. Статистическая оценка включает определение математического ожидания статистических величин, выведенных из выборок совокупности. Впрочем, при анализе с помощью временных рядов обычно доступны не выборки генеральной совокупности, взятые одновременно, а дискретные данные, полученные как функция времени. Этот момент обычно полагается несущественным, поскольку принимается эргодическая гипотеза: свойства данных временного ряда совпадают со свойствами предполагаемых выборок. Приведем несколько статистических определений.

Среднее значение временного ряда, состоящего из элементов данных x(n), n = 0,1,..., N-1, равно его математическому ожиданию Е[х(п)]:

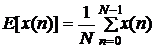где Е – оператор математического ожидания. Дисперсия того же ряда выражается как

Автоковариационная матрица x(n) записывается следующим образом:

где через m обозначено запаздывание элементов данных, а через x(n) записано Е[х(п)]. Предполагая конечную реализацию, спектральную плотность мощности можно записать как

Отметим, что если в отличие от бесконечно длительных стохастических процессов рассматривать сигналы конечной длительности, более правильным будет использовать спектральную плотность энергии. Спектральная плотность мощности имеет размерность B²Гц^-1 . Если оценивается статистический параметр α, смещение (отклонение) оценки определяется как разность истинного значения (взятого из генеральной совокупности) и

оценки:

смещение = α – Е[α].

Если смещение равно нулю, оценка совпадает с истинным значением; если смещение не равно нулю, оно представляет ошибку определения α и оцененное значение α называется смещенным. Хорошие алгоритмы оценки смещения не допускают. Дисперсия α является мерой ширины максимума функции распределения плотности вероятности α. При небольшой дисперсии пики довольно узкие, а при дисперсии, стремящейся к нулю, оцененное значение стремится к значению из генеральной совокупности (истинному), если оценка не смещена. Если дисперсия стремится к нулю при увеличении числа элементов данных N, оценку называют состоятельной. Если она несостоятельна, оценки будут флуктуировать с увеличивающейся амплитудой от реализации к реализации с увеличением элементов данных. Следовательно, нужно, чтобы статистические оценки были несмещенными и состоятельными.

Показано, что оценки спектра, выведенные как периодограммы, несостоятельны, т.е. последовательные реализации дают флуктуирующие оценки, несмещенные только для больших наборов данных. Для получения устойчивых и более точных оценок вырезаются блоки данных, спектры которых затем усредняются. Данная идея реализована в методе модифицированных периодограмм Барлетта и Уэлша. В заключение рассмотрен непараметрический метод Блэкмена-Тьюки. Метод заключается в следующем: вначале вычисляется взвешенная автокорреляционная функция данных, и по ее БПФ получается энергетический спектр. Оценка спектра по методу Блэкмена-Тьюки характеризуется большей добротностью, чем другие методы с использованием периодограмм.

Кроме того, следует определить добротность оценок спектральной плотности мощности, что позволит сравнить различные оценки. В качестве выражения для добротности оценки было предложено отношение квадрата среднего спектральной плотности мощности к ее дисперсии:

Принципы оценки спектра

Рассмотрим форму сигнала напряжения в зависимости от времени. Данная форма сигнала может дать полезную информацию. Например, это может быть синусоида, которую естественно характеризовать ее амплитудой, частотой и фазой. Точнее, такой сигнал можно считать состоящим из одной гармоники известной частоты с определенной амплитудой и фазой. В качестве альтернативы представления сигнала как функции напряжения от времени его можно представить двумя графиками: зависимости амплитуды от частоты и зависимости фазы от частоты. Поскольку синусоида – это единственный сигнал, который имеет одну амплитуду, одну фазу и одну частоту, на графиках амплитуды и фазы синусоиды будет расположена одна точка. С помощью анализа Фурье можно показать, что все сигналы можно математически представить как сумму синусоидальных сигналов, каждый из которых имеет свою амплитуду и фазу на заданной частоте. Следовательно, любой сигнал можно альтернативным образом представить зависимостью амплитуды от частоты и фазы от частоты Данные графики называются амплитудным и фазовым спектрами. Данные спектра важны, поскольку они предлагают дополняющий способ представления сигнала, из которого яснее видна информация о частотном содержании сигнала. Наблюдаемые формы спектров и изменения в них весьма полезны при понимании и интерпретации сигналов. Амплитудный и фазовый спектры в свою очередь очень часто дают больше полезной информации, чем сигналы. Тема преобразования из временной области в частотную и обратно описана в лабораторной работе 2. Были изложены концепции преобразования периодически сигналов в частотную область с помощью ряда Фурье и комплексного ряда Фурье. Там же было показано, что частоты синусоидальных компонентов периодического сигнала, известные как Фурье-компоненты, гармонически связаны друг с другом, т.е. каждый кратен первой гармонике f, где

f = 1/T_p

где Т_p – период повторения сигнала. Известно, что расстояние между любой парой соседних гармоник одинаково и равно f = 1/T_p, так что данная величина называется еще разрешением по частоте или частотным разрешением. Амплитуда амплитудного спектра измеряется в вольтах.

Непериодические, но непрерывные сигналы можно преобразовать из временной в частотную область с использованием преобразования Фурье. Было показано, что «амплитуда» этого преобразования имеет размерность ВГц^-1 и, если изобразить ее в зависимости от частоты, получим амплитудный спектр. Следовательно, площадь под кривой между двумя частотами характеризует «среднее» напряжение сигнала для частотных компонентов, лежащих между указанными двумя частотами. Возводя в квадрат «амплитуды» вычисленных Фурье-компонентов, получим спектральную плотность энергии сигнала в ДжГц^-1. Термином «спектр» часто называют графики зависимости спектральной плотности амплитуды и спектральной плотности энергии от частоты.

Если рассматриваемый сигнал длителен по сравнению с интервалом времени, в течение которого можно считать, что сигнал имеет постоянные статистические моменты, оценка спектра с большой вероятностью будет неточной. Сказанное также справедливо в том случае, когда сигнал сильно зашумлен. В таких ситуациях необходимо сгладить оцененный спектр, чтобы получить улучшенную оценку, поскольку сглаживание спектра позволяет устранить элемент случайности. Отношение сигнал-шум в случайных сигналах можно улучшить путем усреднения сигналов; при усреднении К сигналов отношение сигнал-шум улучшается в раз.

Итак, один метод повышения точности оценки спектра уже есть: разделить данные на К частей равной длины, определить спектр каждой части, а затем усреднить полученные спектры. Таким образом получаются средняя амплитуда и средняя фаза каждого гармонического частотного компонента К спектров, графическое представление которых является спектром средних амплитуды и фазы. Точность спектров можно выразить через их дисперсию. Например, чем меньше дисперсия спектральной плотности мощности, чем точнее оценка. Следовательно, важно знать, как влияет метод оценки спектра на его дисперсию. Далее объясняется, что оценка спектра как среднего спектров К частей данных имеет меньшую дисперсию, чем оценка, вычисленная непосредственно, причем дисперсия уменьшается пропорционально числу частей. Даже если шумовая составляющая сигнала мала, т.е. имеем большое отношение сигнал-шум, результат, усредненный по К частям, по-прежнему значительно повышает точность этого метода модифицированных периодограмм. В то же время, разбиение данных на части приводит к тому, что при вычислении БПФ используется меньше выборок, а следовательно, оценка спектра получается более грубой. Этого недостатка можно избежать, введя дополняющие нули. Итак, всегда нужно помнить, что требования к точности оценки и необходимой спектральной гладкости противоречивы, и добиваться наилучшего компромисса между ними. Другой подход к сглаживанию графиков спектральных функций – это вычислить его по ДПФ взвешенной автокорреляционной функции данных. Этот принцип положен в основу метода Блэкмена-Тьюки. Поскольку автокорреляционная функция данных состоит из среднего сумм произведений данных и запаздывающих копий самих себя, отношение сигнал-шум улучшается. Метод Блэкмена-Тьюки дает спектр с большей добротностью, чем спектр, полученный методами модифицированных периодограмм.

Взвешивающие функции также оказывают сглаживающий эффект на спектр. В частности, функции с небольшими боковыми лепестками в частотной области отфильтровывают шум, который не входит в основной лепесток, и предлагают улучшенное сглаживание. Фактически для реализации этой разновидности спектрального сглаживания нужно свернуть спектр данных со спектром выбранной взвешивающей функции.

Параметрические методы оценки спектра не настолько требуют присутствия человека, как непараметрические методы, и их можно автоматизировать. Ниже описано, как с помощью параметров модели сформировать модель данных, на основе которой по функциям частотных характеристик линейных систем можно получить спектр данных.

Традиционные методы

Особенности и нежелательные эффекты

Частота дискретизации и наложение. Выполнению спектрального анализа должна предшествовать передача аналоговых сигналов через фильтр защиты от наложения спектров, задача которого – предотвратить наложение дискретного сигнала после последующего этапа аналого-цифрового преобразования. Наложением называется искажение спектра сигнала при вводе паразитных (побочных) низкочастотных компонентов вследствие объединения недостаточного фильтра защиты от наложения спектров и слишком низкой частоты дискретизации.

Рис. 1. Спектральная плотность амплитуды сигнала с равномерной спектральной плотностью

«Гребешковое искажение», или «эффект частокола». Дискретное преобразование Фурье (ДПФ) выдает гармонические амплитудные и фазовые компоненты, равномерно размещенные по шкале частот. Густота размещения спектральных линий уменьшается с увеличением длины дискретизованного сигнала. Следовательно, если компонент сигнала расположен между двумя соседними частотными гармониками спектра, представить его надлежащим образом нельзя. Энергия такого компонента будет распределена между соседними гармониками, что приведет к искажению близлежащих спектральных «амплитуд». Спектральная плотность амплитуды равномерно распределенного сигнала показана на рис.1. Отметим конечную ширину основных лепестков, центрированных на гармонических частотах, и то, что компонент сигнала на такой негармонической частоте, как f_nh, нельзя представить надлежащим образом. Для решения этой проблемы гармонические компоненты должны размещаться более тесно и совмещаться с частотами сигнала. Этого можно достичь, введя в реальные данные дополнительные нули. Эти нули называются дополняющими и нужны для увеличения точности – приближения оцененного спектра к истинному спектру без использования дополнительной информации. Итак, к N данным требуется добавить такое количество нулей N’, чтобы удовлетворялось условие:

N+N’=2^m

в алгоритме двоичного быстрого преобразования Фурье (БПФ), где m – целое. Кроме того, гармоники частоты l/(N+N’–1)Т, где T представляет интервал дискретизации, должны совпадать с частотами сигнала.

Чтобы представить максимальное снижение выигрыша от обработки, которое возникает на частотах, расположенных посредине между гармонически связанными частотами, определяется гребешковое искажение (scalloping loss) (ГИ):

где W представляет ДПФ-образ весовой функции, – циклическая частота дискретизации, – частота дискретизации, N – число элементов данных, n – номер элемента данных, – весовая функция, дискретизованная во временной области.

Как уже отмечалось, конечная длина данных ограничивает возможное разрешение по частоте до l/(N – 1)T (Гц). В результате получается грубый спектр, который можно сгладить и сделать непрерывным, используя дополнительные нули. Данный процесс является просто интерполяцией спектральной кривой между соседними гармониками. Действительного улучшения разрешения можно добиться только за счет более длительной реализации. После дополнения N' нулями интервал частот между линиями спектра становится равным l/(N + N' – 1)T (Гц).

Исключение тренда. Перед вычислением спектра нужно удалить все тренды в данных, поскольку вектор ошибок, из-за которого к данным добавляются тренды, будет интегрироваться и может породить большие ошибки в оцененном спектре.

Просачивание спектральных составляющих и размывание спектра. БПФ, которое применяется к набору дискретных данных, – это не совсем истинное БПФ процесса, из которого получены данные. Это объясняется тем, что процесс непрерывен, тогда как данные имеют начало и конец, которые определяются выбранной реализацией. Для эффективного получения данных, которые представляют сигнал длительностью T_s(s), все дискретные значения в интервале T_s умножаются на единицу, а все данные вне этого интервала умножаются на нуль. Это эквивалентно умножению (или взвешиванию) сигнала на прямоугольный импульс (взвешивающую, или весовую, функцию) ширины T_s и высоты 1. В этом случае выборки данных v(n) равны произведению элементов данных s(n) и значений весовой функции :

v(n) = s(n).

Произведение во временной области эквивалентно свертке в частотной. Следовательно, БПФ-образ n-й гармоники равен

где – циклическая частота n-й гармоники, – комплексный ДПФ-компонент на частоте , – ДПФ-образ функции на частоте , – действительный ДПФ-компонент сигнала на частоте .

Из уравнения следует, что рассчитанный спектр состоит из истинного спектра данных, свернутого со спектром весовой функции. Амплитудный спектр прямоугольного импульса записывается следующим образом (данное выражение называется также ядром Дирихле):

Здесь – функция выборки с частотой . Она состоит их основного лепестка и бесконечного числа боковых лепестков с максимумами на 0 Гц и (n+0,5)/T_s Гц соответственно. Теперь амплитудный спектр отдельного синусоидального компонента сигнала на частоте f_n включает в себя два импульса на частотах ±f_n. Свертка с дискретизирующей функцией дает спектр, изображенный на рис.2. Два импульса преобразовались в две перекрывающиеся выборочные функции. Влияние прямоугольной весовой функции проявилось во введении в вычисленный спектр побочных максимумов (из-за влияния боковых лепестков). Такой эффект будет иметь место для каждого частотного компонента сигнала, так что амплитудный спектр сигнала будет искажен из-за перекрестного сложения и вычитания большого числа боковых и главных лепестков весовых функций. Вследствие этого могут появиться ложные или скрыться истинные максимумы спектра. Данный эффект называется просачиванием спектральных составляющих. Для того чтобы избежать его, данные следует модифицировать – умножить на весовую функцию, форма которой предназначена для снижения влияния боковых лепестков. Подходящая функция равна 1 в центральной точке и сходит на нуль в точках n = 0 и n = N – l. На настоящий момент разработано по крайней мере 23 такие функции.

Чтобы минимизировать просачивание спектральных составляющих, форма весовой функции выбирается с минимальными уровнями боковых лепестков. К сожалению, это приводит к увеличению ширины основного лепестка, так что он расширяется на соседние боковые лепестки (происходит наложение). Данный эффект имеет место для всех гармоник, а общий результат – наложение спектра сигнала, или размывание. Таким образом, весовые функции и их параметры надлежит выбирать тщательно, чтобы добиться оптимального баланса между разрешением по частоте и статистической точностью оценки спектра.

Рис. 2. Спектральная плотность амплитуды синусоидального сигнала,

свернутого с дискретизующей функцией

Дата добавления: 2018-04-05; просмотров: 583; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 Следующая ⇒

Мы поможем в написании ваших работ!