Физические процессы в цепях переменного тока с при последовательном соединении R

Уравнение напряжений для цепи рис. 2.11, а имеет видŪ = Ū_r + Ū_L+ Ū_C.

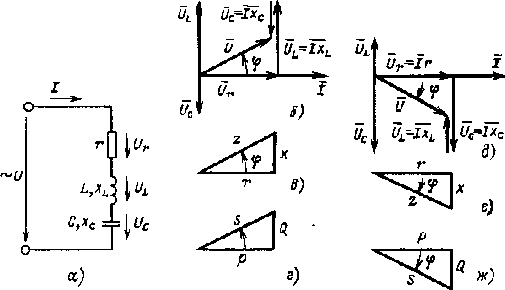
Рис. 2,11, Электрическая цепь, содержащая последовательно включенные r, L и С (а), ее векторная диаграмма (б), треугольники сопротивлений и мощностей (в и г) цепи при x_L> x_C, векторная диаграмма (д), треугольники сопротивлений и мощностей(e и ж) цепи при x_C > x_L

Векторные диаграммы для цепи рис. 2.11, а изображены на рис. 2,11, б и в. Вектор напряжения на активном сопротивлении Ū_rсовпадает с вектором тока, вектор напряжения на индуктивности Ū_Lопережает вектор тока на 90°, вектор напряжения на емкости Ū_С отстает от вектора тока на 90°. Следовательно, между векторами напряжения на индуктивности и емкости образуется угол 180°.

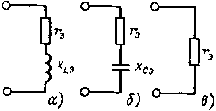
Рис. 2.12. Эквивалентные схемы цепи, изображенной на рис. 2.11, а: а - х_L > х_С; б - х_С >x_L; в - х_L = х_С

Если x_L > х_С, то и U_L > U_С и векторная диаграмма будет иметь вид, изображенный на рис. 2.11, б, а треугольник сопротивлений — на рис. 2.11, в, где x = x_L - x_С. Если х_С > х_L, то U_C > U_L и векторная диаграмма будет иметь вид, изображенный на рис. 2.11, д, а треугольник сопротивлений — на рис. 2.11, е, где х = х_С - x_L. Значение напряжения, приложенного к цепи,

(2,23)

U = √(U_r)² + (U_L - U_C)².

Выразив в (2.23) напряжение через ток и сопротивления, получим

U = √(I_r)² + (Ix_L - Ix_C)² = I√r² + (x_L - x_C)².

Последнее выражение представляет собой закон Ома для последовательной цепи r, L, С:

I =	U	=	U	.
	√r² + (x_L - x_C)²		z

где z = √r² + (x_L - x_C)² = √r² + x² — полное сопротивление цепи, Ом; х — реактивное сопротивление цепи, Ом.

На основании проведенного анализа цепи, состоящей из последовательно соединенных r, L, С,можно сделать следующие выводы.

Если x_L > x_С, то напряжение сети опережает по фазе ток на угол φ:u = U_m sin (ωt + φ).Цепь имеет активно-индуктивный характер.

Цепь может быть заменена эквивалентной цепью, изображенной на рис. 2.12, а. В эквивалентной схеме r_э = r, х_э = x_L - x_С = x_L_э.

Если x_С > x_L, то напряжение сети отстает по фазе от тока на yгол φ:и = U_m sin (ωt - φ).Цепь имеет активно-емкостный характер.

Цепь может быть заменена эквивалентной цепью, изображенной на рис. 2.12, б. В эквивалентной цепи r_э = r, x_э = х_C - х_L = x_C_э.

Векторные диаграммы. Расчетные соотношения. Резонанс напряжений.

Векторный метод изображения синусоидально изменяющихся величин. При изучении процессов, происходящих в цепях переменного тока, удобно пользоваться методом векторного изображения синусоидально изменяющихся величин. Этот метод основан на том, что при вращении некоторого вектора OA (рис. 1, а) с равномерной угловой скоростью проекция ОВ этого вектора на неподвижную вертикальную ось у — у пропорциональна синусу угла wt, образованного вектором OA с горизонтальной осью х , т. е. ОВ = ОА sin wt. Следовательно, кривая, выражающая зависимость длины проекции ОВ от угла wt за один оборот вектора OA, будет представлять собой синусоиду (рис. 1,б). Если в качестве длины (модуля) вектора принять амплитудное значение переменного тока Im, то полученная кривая будет представлять собой графическое изображение изменения мгновенного значения тока I от угла wt. При wt = 0 (точка 1) вектор OA будет расположен горизонтально и i = 0; при wt = 90° (точка 2) вектор OA расположен вертикально вверх и i = I_т при wt =180° (точка 3) вектор OA также расположен горизонтально и i = 0; при wt = 270° (точка 4)

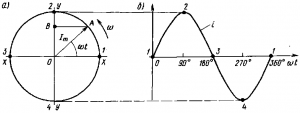Рис. 1. Изображение синусоидально изменяющегося тока: а — вращающимся вектором; б — в виде кривой

вектор OA расположен вертикально вниз и i=—I_т (проекции ОВ вектора OA, расположенные выше точки 0, будем считать положительными, а расположенные ниже этой точки — отрицательными). Точкам 1—4, а при различных положениях вращающегося вектора OA соответствуют точки 1—4 на кривой изменения тока i (см. рис. 1,б). Направление вращения векторов условно принимают против часовой стрелки, поэтому углы wt, которые отсчитывают в направлении вращения векторов, считают положительными, а против этого направления — отрицательными. В случае если требуется получить векторное изображение нескольких синусоидально изменяющихся величин, например двух токов i₁ и i₂, чертят два вращающихся вектора ОА₁ и ОА₂ (рис. 2, а) с различными модулями 1_т1 и 1_т2Если в момент начала отсчета синусоидально изменяющаяся величина не равна нулю, а имеет некоторое значение I_т sin α₁ (рис. 2,б), то вектор ОА₁ в начальный момент при фазе wt = 0 образует с горизонтальной осью некоторый угол α₁ Этот угол называется начальным фазным углом, или начальной фазой. Разность начальных фаз синусоидально изменяющихся величин называют сдвигом фаз, или углом сдвига фаз. Например, синусоида

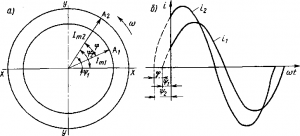Рис. 2. Изображение двух синусоидально изменяющихся токов: а — вращающимися векторами; б — в виде кривых

тока i₁ имеет начальную фазу φ₁, а синусоида тока i₂— начальную фазу φ₂ Следовательно, токи i₁ и i₂сдвинуты друг относительно друга по фазе на угол φ = φ₁ — φ₂. Это означает, что каждая точка синусоиды тока i₁ сдвинута относительно соответствующей точки синусоиды тока i₂ на угол φ. При векторном изображении токов i₁ и i₂ сдвиг фаз между ними выражается в виде угла φ между векторами ОА₁ и ОА₂.Из. рис. 2,а и б видно, что вектор OА₂ при своем вращении идет впереди вектора ОА₁, т. е. ток i₂при своем изменении достигает нулевых и максимальных значений раньше, чем ток i₁. Следовательно, ток i₂ опережает по фазе ток i₁ на угол φ. Можно также считать, что ток i₁ отстает от тока i₂ на угол φ. Если же две синусоидально изменяющиеся величины, например токи i₁ и i₂, одновременно проходят через нулевые и максимальные значения, то говорят, что они совпадают по фазе. В этом случае они изображаются двумя совпадающими по направлению векторами (φ = 0). Векторы, изображающие синусоидально изменяющиеся токи, напряжения и э. д. с, обозначаются соответствующими буквами с точкой над обозначением. Явление резонанса. Электрическая цепь, содержащая индуктивность и емкость, может служить колебательным контуром, где возникает процесс колебаний электрической энергии, переходящей из индуктивности в емкость и обратно. В идеальном колебательном контуре эти колебания будут незатухающими. При подсоединении колебательного контура к источнику переменного тока угловая частота источника w может оказаться равной угловой частоте w₀, с которой происходят колебания электрической энергии в контуре. В этом случае имеет место явление резонанса, т. е. совпадения частоты свободных колебаний w₀, возникающих в какой-либо физической системе, с частотой вынужденных колебаний w, сообщаемых этой системе внешними силами. Резонанс в электрической цепи можно получить тремя способами: изменяя угловую частоту w источника переменного тока, индуктивность L или емкость С. Различают резонанс при последовательном соединении L и С — резонанс напряжений и при параллельном их соединении — резонанс токов. Угловая частота w₀, при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура. Резонанс напряжений. При резонансе напряжений (рис. 1, а) индуктивное сопротивление X_Lравно емкостному Х_с и полное сопротивление Z становится равным активному сопротивлению R. В этом случае напряжения на индуктивности U_L и емкости U_c равны и находятся в противофазе (рис. 1,б), поэтому при сложении они компенсируют друг друга. Если активное сопротивление цепи R невелико, ток в цепи резко возрастает, так как реактивное сопротивление цепи X = X_L—X_с становится равным нулю. При этом ток I совпадает по фазе с напряжением U и I=U/R. Резкое возрастание тока в цепи при резонансе напряжений вызывает такое же возрастание напряжений U_L и U_c, причем их значения могут во много раз превышать напряжение U источника, питающего цепь. Угловая частота w0, при которой имеют место условия резонанса, определяется из равенства w_oL = 1/(w₀С).

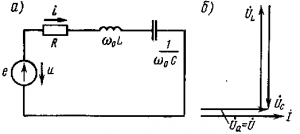Рис. 1. Схема (а) и векторная диаграмма (б) электрической цепи, содержащей R, L и С, при резонансе напряжений

Отсюда имеем

w_o = 1/w(LC)

Если плавно изменять угловую частоту w источника, то полное сопротивление Z сначала начинает уменьшаться, достигает наименьшего значения при резонансе напряжений (при w_o), а затем увеличивается (рис. 1, а). В соответствии с этим ток I в цепи сначала возрастает, достигает наибольшего значения при резонансе, а затем уменьшается.

Дата добавления: 2018-04-04; просмотров: 989; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 7 8 9 10 111213 14 15 16 Следующая ⇒

Мы поможем в написании ваших работ!